【重新认识数据结构】之优先队列

Hello，大家周末好，我是猿码！

刷算法题中，我经常会碰到一些题使用队列比较其它数据结构更方便，其中优先队列为最！下面我将从队列接口到其子类优先队列来为大家介绍，如有不足之处，还请指出，共成长！

---

队列（Queue）

介绍：

• 接口（interface）
• 继承自 Collection，因此它是 Collection 的子类，且具备 Collection 的一般功能

它是一种为存储过程优于执行过程而设计的集合，其提供数据插入、数据交互以及数据检查机制。

队列中，每个方法存在 2 种形式：其一会因为操作失败而抛出异常，其二则不然，而是以返回一个 null 值结束，当然它们的执行结果依赖于我们如何操作数据。后者对于数据插入来说，有着队列初始容量的严格限制；通常来讲，Queue 的数据插入操作是不可能失败的。

下面是队列的方法及介绍：

boolean add(E e);

— 继承自其父类 Collection。返回结果有两种：true 或 抛出 IllegalStateException、ClassCastException、NullpointException、 IllegalArgumentException 异常。第一个异常出现于若当前没有多余的容量或超出定义的初始容量。一般其 LinkedBlockingQueue 实现会抛出该异常。

boolean offer(E e); // 向 Queue 实例中插入一条数据

— Queue 接口的自有方法，区别于 add 方法的是，它不会在超出初始容量时抛出 IllegalStateException，取而代之的是返回 false 结束。

E remove(); 

— 继承自 Collection。返回值有两种： E 泛型返回值或当队列中没有数据时调用 remove 会抛出 NoSuchElementException。 

E poll();  // 移除位于队列头部的 1 条数据

— Queue 接口的自有方法，区别 remove 的是当队列为空调用 poll 只会返回 null ，而不抛出异常。

队列的 FIFO 与 LIFO 定义

FIFO

LIFO 

— 一般地，我们都会听说队列是先进先出(FIFO) ，栈是先进后出(LIFO)。如果你的老师这么跟你说，证明你的老师就是一打工的！下面我们一起看看官方怎么说的：

Queues typically, but do not necessarily, order elements in a FIFO(first-in-first-out) manner. Among the exceptions are priority queues, which order elements according to a supplied comparator, or the elements' natural ordering, and LIFO queues (or stacks) which order the elements LIFO(last-in-first-out);

— 翻译过来大致就是：Queues 通常不会也非必须遵循 FIFO 机制，比如优先队列就是这些情形中的一个栗子。它的元素排序机制依赖于是否在初始化其实例时传入 Comparator 参数，这将决定其排序是基于 Comparator 或自然排序。而另一种队列 Stack 则遵循 LIFO 排序机制（因为它没有可传入自定义排序机制的构造函数）。

Queue 的介绍就到这里，下面我来一起看看其实现之一 PriorityQueue。

---

队列（PriorityQueue）

介绍

优先队列是无界(Unbounded)队列的一种，基于优先堆(Priority Heap)实现。

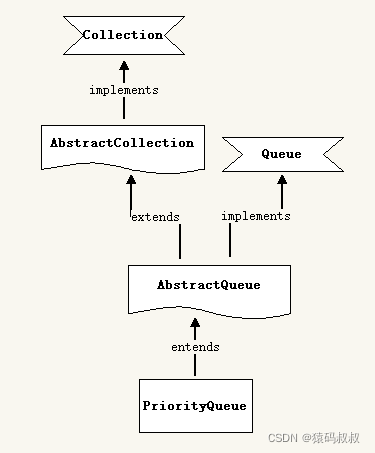
继承与实现结构：

 下面我将先围绕堆，然后是优先队列的核心方法，来分析以及如何使用PirorityQueue。

堆

关于堆，我们在初学 Java 时，JVM 的内存模型中就有堆的概念。JVM 中的堆是存储创建对象的真实数据的地方。而这里的堆是一棵完全二叉树实现的数据结构。

属性

• 常见有大顶堆、小顶堆两种
• 根节点的值是所有节点中最大（大顶堆）或最小（小顶堆）的值
• 父节点的值只能大于等于（大顶堆）或小于等于（小顶堆）其左右子节点的值。其中等于的情况不是必须，它取决于元素的插入顺序，比如 [1，2，2，2]，4 个元素创建一个小顶堆或大顶堆，就会出现父子节点相等的情况
• 大顶堆与小顶堆始终保持根节点最大或最小，父节点大于等于或小于等于左右子节点这一特性，但不保证有序。因此我们可以说：大顶堆与小顶堆是无序的

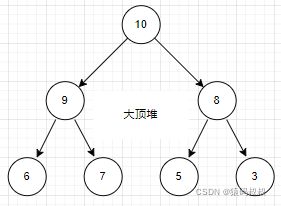
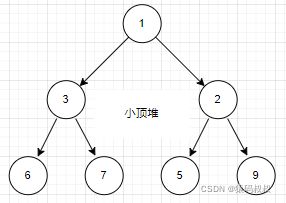
大顶堆：                                                              小顶堆

            

 堆与普通树的区别

          二叉搜索树

 

• 存储与执行过程：堆只侧重存储过程，二叉搜索树则是侧重于存储过程与执行过程。比如获取最大值，我们预先创建一个大顶堆，当将 n 个元素存入大顶堆时，目标值经存储过程完成后找到并放置堆顶。而二叉搜索树，则不然，它要按照左子节点总是小于父节点，右子节点总是大于父节点这一特性来存储元素，同时也会按照这个顺序去执行搜索。两者的作用很明显
• 节点顺序：堆中的根节点始终为所有元素中最大或最小，二叉搜索树则不是。堆：（父节点 >= | <= 左右子节点 & 左子节点 ？右子节点(? 代表无特定关系)）；二叉搜索树：（左子节点 <= 父节点 <= 右子节点 & 左子节点 <= 右子节点）
• 内存占用：树有左右指针，因此在为其每个节点分配内存时，还要为其左右指针分配内存空间；而堆只需要用一个数组，无需指针
• 时间复杂度：堆由于不需要搜索，因此在获取元素时只需要 O(1) 的常量时间，而二叉搜索树的元素获取则需要进行搜索，由于具有二段性，因此需要O(log n) 的时间

堆的元素存储（此处参考某位大佬的笔记，致敬）

刚才说到，堆用一个数组存储即可，比如上图的大顶堆，转成数组如下：

int[] heapArray = {10, 9, 8, 6, 7, 5, 3};

那么问题来了，怎么确定哪个元素是根节点，哪个元素是父或左右子节点呢？

有如下公式：

parent [ i ] = queue [ floor ( (i - 1) / 2) ]

left [ i ] = queue [ 2 * i + 1 ]

right [ i ] = queue [ 2 * (i + 1) ]

下面我们构建一个列表，来分别检测该公式的有效性：

Node(val)	Index	Parent(index)	Left(index)	Right(index)
10	0	(0 - 1) / 2	2 * 0 + 1	2 * 0 + 2
9	1	(1 - 1) / 2	2 * 1 + 1	2 * 1 + 2
8	2	(2 - 1) / 2	2 * 2 + 1	2 * 2 + 2
6	3	(3 - 1) / 2	2 * 3 + 1	2 * 3 + 2
7	4	(4 - 1) / 2	2 * 4 + 1	2 * 4 + 2
5	5	(5 - 1) / 2	2 * 5 + 1	2 * 5 + 2
3	6	(6 - 1) / 2	2 * 6 + 1	2 * 6 + 2

Tip：对于以上公式计算出来的结果，如果该结果不存在于索引中，意味着该索引没有元素，或不存在该节点，比如根节点的父节点计算出的结果为 -1，意味着根节点不存在父节点

堆的介绍就到这里。由于优先队列（PriorityQueue）是完全基于堆实现的，因此当你理解了上面的堆的相关介绍，优先队列理解起来就容易很多。下面呢，我将围绕 PriorityQueue 的相关 API 来进一步了解其功能以及使用场景。

优先队列的 API 与应用场景

成员变量：

/**
* Priority queue represented as a balanced binary heap: the two
* children of queue[n] are queue[2*n+1] and queue[2*(n+1)].  The
* priority queue is ordered by comparator, or by the elements'
* natural ordering, if comparator is null: For each node n in the
* heap and each descendant d of n, n <= d.  The element with the
* lowest value is in queue[0], assuming the queue is nonempty.
*/
transient Object[] queue; // non-private to simplify nested class access

— ：该数组，就是用于存储堆元素的。注释中的翻译大致就是：优先队列作为一个平衡堆，其左子节点在 queue[n] 中为 queue[2 * n + 1]，右子节点为 queue[2 * (n + 1)]。排序是基于 Comparator 或自然排序。若 Comparator 为 null，则默认为小顶堆，最小的元素处于堆顶端 queue[0] 的位置。

    /**
     * The comparator, or null if priority queue uses elements'
     * natural ordering.
     */
    private final Comparator comparator;

— ：comparator 成员变量用于决定优先队列的排序规则，一般在调用构造函数时可选择性的传入该参数。

    /**
     * The maximum size of array to allocate.
     * Some VMs reserve some header words in an array.
     * Attempts to allocate larger arrays may result in
     * OutOfMemoryError: Requested array size exceeds VM limit
     */
    private static final int MAX_ARRAY_SIZE = Integer.MAX_VALUE - 8;

—： 优先队列的最大存储容量限制在 ，与 ArrayList 一样。这么做是为了避免 OOM(Error)。由于我们写的代码会放到不同的虚拟机 (VMs) 上运行，而某些虚拟机会需要额外的空间来存储（Header information）也就是注释中的 Header words，即标头信息，因此我们需要为此预留一些空间，来避免超出 VM 限制。现实中热胀冷缩就是解释这一问题的典型例子。

方法：

private void initFromPriorityQueue(PriorityQueue c);

—： 该方法用于将一个优先队列中的所有元素拷贝至另一个优先队列中。

    private void grow(int minCapacity) {
        int oldCapacity = queue.length;
        // Double size if small; else grow by 50%
        int newCapacity = oldCapacity + ((oldCapacity < 64) ?
                                         (oldCapacity + 2) :
                                         (oldCapacity >> 1));
        // overflow-conscious code
        if (newCapacity - MAX_ARRAY_SIZE > 0)
            newCapacity = hugeCapacity(minCapacity);
        queue = Arrays.copyOf(queue, newCapacity);
    }

—： 该方法，用于优先队列的扩容。如果原始容量小于 64，就增加原来的 1 倍，反之只增加原来的  。下面的 overflow-concious 是溢出检测。如果 minCapaccity < 0，说明溢出；若 minCapacity > ，就将其改为 , 反之不变。

    public boolean add(E e) {
        return offer(e);
    }

    public boolean offer(E e) {
        if (e == null)
            throw new NullPointerException();
        modCount++;
        int i = size;
        if (i >= queue.length)
            grow(i + 1); // 扩容
        size = i + 1;
        if (i == 0)
            queue[0] = e;
        else
            siftUp(i, e); // 添加元素的核心方法
        return true;
    }

—： add 是 Collection 接口的方法，offer 是队列（Queue）的方法，siftUp 才是其自有方法。而 siftUp中又会根据当前 comparator 成员变量是否为 null，分别调用 siftUpComparable 和 siftUpUsingComparator 两个方法。下面我们一一介绍。

   // comparator 不为 null 时调用 
   private void siftUpUsingComparator(int k, E x) {
        // 判断是否是初次插入元素
        while (k > 0) {
            // 根据公式 (n - 1) / 2 求出当前 k 索引的父节点索引
            int parent = (k - 1) >>> 1;
            // 取出父节点值
            Object e = queue[parent];
            // 比较 x（要插入的元素）是否大于或小于其父节点，如果 true 就结束循环
            // 意味着将元素插入尾部即可
            if (comparator.compare(x, (E) e) >= 0)
                break;
            // 如果比父节点大或小(基于 Comparator 如何定义)，则原父节点的位置替换为 x
            queue[k] = e;
            // 同时将 k 变为 parent 索引，反复执行，知道满足上面的哪个 break 条件
            k = parent;
        }
        // 最后结束循环，k 即为正确要插入的位置
        queue[k] = x;
    }

—： 这个方法的大致功能，理解起来其实不难，毕竟是数组结构。但其中的 >>> 位运算符，顺带讲一下。如果你用 100 个数字对其进行 >>> 1 操作，那么得出的结果为 (i / 2)，其中每一对连续的偶奇数字（指的是从 0 开始，0 和 1 为一对偶寄数字，2 和 3 为一对偶奇数字）的计算结果是一样的，意味着通过运算符 n 可以计算出 n / 2 个唯一数字以及 (n / 2) 个 连续相同的数字对。

    private void siftUpComparable(int k, E x) {
        Comparable key = (Comparable) x;
        while (k > 0) {
            // 同 siftUpUsingComparator 方法
            int parent = (k - 1) >>> 1;
            Object e = queue[parent];
            // 这里的 Comparable 没有自定义，因此默认结果是 x 比计算的父节点大，就结束循环
            // 因此，若不传入 Comparator 默认是小顶堆
            if (key.compareTo((E) e) >= 0)
                break;
            queue[k] = e;
            k = parent;
        }
        queue[k] = key;
    }

—： 这个方法重点理解的地方就是 Comparable 的默认比较规则与 Comparable 的使用方法

    private E removeAt(int i) {
        // assert i >= 0 && i < size;
        modCount++;
        // 每移除 1 个元素，size 相应 -1
        int s = --size;
        // 如果移除的是最后一个元素
        if (s == i) // removed last element
            queue[i] = null;
        else {
            // 获取最后一个元素
            E moved = (E) queue[s];
            // 将尾部节点置空，由于移除了某个位置的元素，堆数组需向数组左侧调整
            queue[s] = null;
            // 先调整尾部即大于 size >>> 1 的所有元素
            siftDown(i, moved);
            if (queue[i] == moved) {
                siftUp(i, moved);
                if (queue[i] != moved)
                    return moved;
            }
        }
        return null;
    }

—： 该方法是根据提供的索引，删除该位置的元素。由于是数组，因此我们需要按照原有规则去调整移除某个元素后的数组。该方法中的 siftUp 调用，还需要进一步细究，此处就不贴为何调用，如果有哪位老师知道原理，可以留言。

下面我们看看，siftDown 方法的具体调用。该方法同样是设置了自定义排序规则与否的 2 中调用。

    private void siftDownUsingComparator(int k, E x) {
      
        int half = size >>> 1;
        // 判断被移除元素的下标是否小于当前 size / 2
        while (k < half) {
            int child = (k << 1) + 1;
            Object c = queue[child];
            int right = child + 1;
            // 如果右子节点下标小于当前 size
            if (right < size && 
                // 且左子节点大于或小于右子节点
                comparator.compare((E) c, (E) queue[right]) > 0)
                // 获取右子节点元素同时改变 child 为右子节点的索引
                c = queue[child = right];
            // 如果 x（数组中最后一个元素）与 c 满足自定义排序规则，意味着
            // 这一块儿调整结束，跳出循环
            if (comparator.compare(x, (E) c) <= 0)
                break;
            // 将子节点的元素放到被移除的元素的位置，由于数组中移除一个元素，其后的
            // 的元素都需要向前移动 1 个索引，因此需要循环解决问题 
            queue[k] = c;
            k = child;
        }
        // 最后将最后一个元素放入调整后的 k 位置
        queue[k] = x;
    }

—： 该方法，理解起来稍微有些绕，致于 siftDownComparable 方法与这个大致一样，这里就不再详述了，下面我重点画一个草图，来描述移除优先队列中某个元素大致流程，以结束该博文的延申。

 —： 可能图画的不是很好，下面我贡献出国外的一个数据结构动态演示的网站，它属于美国旧金山大学大卫·嘉乐教授的个人网站。该网站几乎囊括了所有数据结构的动态演示，对于初学者也包括我自己，是一个很不错的数据结构辅助学习网站。Data Visualization@David Galles

优先队列使用 Comparator 的 Demo：

    void priorityQueueWithUsingComparator() {
        // 小顶堆实现,当然不传参默认就是小顶堆
        PriorityQueue pq1 = new PriorityQueue<>(
                Comparator.comparingInt(a -> a)
        );

        // 大顶堆
        PriorityQueue pq2 = new PriorityQueue<>(
                (a, b) -> b - a
        );
    }

总结

• 如何举一反三，通过一种数据结构来了解其它数据结构
• 如何通过源码结合示意图解读程序的执行流程
• 如何利用你的英语去了解数据结构的核心知识。一般的我们在各大博客上看到大佬们有关各种数据结构的分析文章，除了自己的经验总结外，一大部分都是参考了源码中的注释。因此，如果你的英语还可以，不妨去试试

好了，今天就到这里了，谢谢大的阅读~