LeetCode - #85 最大矩形(Top 100)
文章目录
-
- 前言
- 1. 描述
- 2. 示例
- 3. 答案
-
- 题解 1
- 题解 2
- 关于我们

前言
本题为 LeetCode 前 100 高频题
本题由于没有合适答案为以往遗留问题,最近有时间将以往遗留问题一一完善。
我们社区陆续会将顾毅(Netflix 增长黑客,《iOS 面试之道》作者,ACE 职业健身教练。)的 Swift 算法题题解整理为文字版以方便大家学习与阅读。
LeetCode 算法到目前我们已经更新到 84 期,我们会保持更新时间和进度(周一、周三、周五早上 9:00 发布),每期的内容不多,我们希望大家可以在上班路上阅读,长久积累会有很大提升。
不积跬步,无以至千里;不积小流,无以成江海,Swift社区 伴你前行。如果大家有建议和意见欢迎在文末留言,我们会尽力满足大家的需求。
难度水平:困难
1. 描述
给定一个仅包含 0 和 1 、大小为 rows x cols 的二维二进制矩阵,找出只包含 1 的最大矩形,并返回其面积。
2. 示例
示例 1
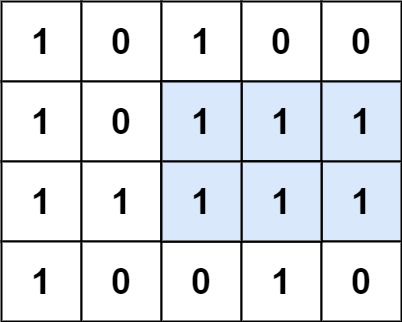
输入:matrix = [["1","0","1","0","0"],["1","0","1","1","1"],["1","1","1","1","1"],["1","0","0","1","0"]]
输出:6
解释:最大矩形如上图所示。
示例 2
输入:matrix = []
输出:0
示例 3
输入:matrix = [["0"]]
输出:0
示例 4
输入:matrix = [["1"]]
输出:1
示例 5
输入:matrix = [["0","0"]]
输出:0
提示:
rows == matrix.lengthcols == matrix[0].length1 <= row, cols <= 200matrix[i][j]为'0'或'1'
3. 答案
题解 1
class Solution {
func maximalRectangle(_ matrix: [[Character]]) -> Int {
if matrix.count == 0 || matrix[0].count == 0{
return 0
}
var ans = 0
var rowArr = Array(repeating:0,count:matrix[0].count + 1)
for y in stride(from:0,to:matrix.count,by:1) {
for x in stride(from:0,to:matrix[0].count,by:1) {
if matrix[y][x] == "1" {
rowArr[x] += 1
} else {
rowArr[x] = 0
}
}
ans = max(ans,getLargetRect(rowArr))
}
return ans
}
func getLargetRect(_ rowArr:[Int]) -> Int {
var stack = [Int]()
var maxArea = 0
for (index,height) in rowArr.enumerated() {
while let last = stack.last, rowArr[last] > height {
stack.removeLast()
var width = 0
if stack.isEmpty {
width = index
} else {
width = index - stack.last! - 1
}
maxArea = max(maxArea, width * rowArr[last] )
}
stack.append(index)
}
return maxArea
}
}
题解 2
class Solution {
func maximalRectangle(_ matrix: [[Character]]) -> Int {
let n = matrix.count
guard n > 0 else {
return 0
}
let m = matrix[0].count
var mark = Array(repeatElement(Array(repeatElement(0, count: m)), count: n))
for i in (0..<n).reversed() {
var count = 0
for j in (0..<m).reversed() {
if matrix[i][j] == "1" {
count += 1
} else {
count = 0
}
mark[i][j] = count
}
}
var result = 0
for i in 0..<n {
for j in 0..<m {
var minColumn = m
var row = i
while row < n && mark[row][j] != 0 {
minColumn = min(minColumn, mark[row][j])
result = max(result, (row - i + 1) * minColumn)
row += 1
}
}
}
return result
}
}
点击前往 LeetCode 练习
关于我们
我们是由 Swift 爱好者共同维护,我们会分享以 Swift 实战、SwiftUI、Swift 基础为核心的技术内容,也整理收集优秀的学习资料。