20利用灰色神经网络预测6个月订单需求(附matlab程序)
1.简述
学习目标:灰色神经网络预测订单需求
灰色系统理论是一种研究少数据、贫信息、不确定性问题的新方法,它以部分信息已知,部分信息未知的“小样本”,“贫信息”不确定系统为研究对象,通过对“部分”已知信息的生成、开发,提取有价值的信息,实现对系统运行行为、演化规律的正确描述和有效监控。
灰色理论强调通过对无规律的系统已知信息的研究,提炼和挖掘有价值的信息,进而用已知信息取揭示未知信息,使系统不断“白化”。
灰色系统中建立的模型称为灰色模型(Grey Model),简称GM模型,该模型是以原始数据序列为基础建立的微分方程。
灰色建模中最有代表性的模型是针对时间序列的GM建模,它直接将时间序列数据转化为微分方程,利用系统信息,使抽象的模型量化,进而在缺乏系统特性知识的情况下预测系统输出。
灰色系统介绍
灰色系统是由华中科技大学的邓聚龙教授于80年代初创立,该系统作为新兴的横断学科,在短短的二十年里已得到了长足的发展。 其已经成为社会,经济,科教,科技等很多领域进行预测,决策,评估,规划,控制,系统分析和建模的重要方法之一。特别是它对于时间序列短,统计数据少,信息不完全系统的建模与分析,具有非常显著的功效。
灰色预测是一种对含有不确定因素的系统进行预测的方法。灰色预测通过鉴别系统因素之间发展趋势的相异程度,即进行关联分析,并对原始数据进行生成处理来寻找系统变动的规律,生成有较强规律性的数据序列,然后建立相应的微分方程模型,从而预测事物未来发展趋势的状况。其用等时距观测到的反映预测对象特征的一系列数量值构造灰色预测模型,预测未来某一时刻的特征量,或达到某一特征量的时间。
灰色系统的基本原理
公理1,差异信息原理
”差异“是信息,凡信息必有差异。
公理2,解的非唯一性原理
信息不完全,不确定的解是非唯一的。该原理是灰色系统理论解决实际问题所遵循的基本法则。
公理3,最少信息原理
灰色系统理论的特点是充分开发利用已占有的”最少信息”。
公理4,认知根据原理
信息是认知的根据。
公理5,新信息优先原理
新信息对认知的作用大于老信息。
公理6,灰性不灭原理
“信息不完全”是绝对的。
2.2 灰生成技术
灰色序列生成:是一种通过对原始数据的挖掘,整理来寻求数据变化的现实规律的途径,简称灰生成。
灰生成特点:在保持原序列形式的前提下,改变序列中的数据的值与性质。一切灰色序列都能通过某种生成弱化其随机性,显现其规律性。
灰生成的作用
- 统一序列的目标性质,为灰决策提供基础。
2.将摆动序列转化为单调增长序列,以利于灰建模。
3.揭示潜藏在序列中的递增势态,变不可比为可比序列。
常见的几种灰色生成类型:
1.累加生成算子(AGO)
2.逆累加生成算子(IAGO)
3.均值生成算子(MEAN)
4.级比生成算子
1.累加生成算子(AGO)
定义 累加生成算子是对原序列中的数据依次累加得到的数列。
2.逆累加生成算子(IAGO)
逆累加生成算子其实就是累减生成,上面是累加,计算步骤跟上面差不多,就是变成了减号罢了。
首先我们先生成序列
3.均值生成算子(MEAN)
看到标题大家可能就知道怎么计算了,我们需要将序列中的前后相邻的两数取平均数,以获得生成新的序列。
我们先简单说明一下模型成立的前提,灰色理论认为一个系统的行为现象虽然是朦胧的,数据是复杂的,但是他一定会包含一定的规律在其中,如果你了解过傅里叶,那么你可以很轻松的理解一个系统暗含规律的情况。灰数的生成就是为了从杂乱的数据中找到规律。因此灰色模型所用的数据是生成数据而非原始数据。
2.代码
%% 清空环境变量
clc
clear
%% 36个样本,每个样本是6个月的销售量
load data
%% 数据累加作为网络输入
[n,m]=size(X);
for i=1:n
y(i,1)=sum(X(1:i,1));
y(i,2)=sum(X(1:i,2));
y(i,3)=sum(X(1:i,3));
y(i,4)=sum(X(1:i,4));
y(i,5)=sum(X(1:i,5));
y(i,6)=sum(X(1:i,6));
end
%% 网络参数初始化
a=0.3+rand(1)/4;
b1=0.3+rand(1)/4;
b2=0.3+rand(1)/4;
b3=0.3+rand(1)/4;
b4=0.3+rand(1)/4;
b5=0.3+rand(1)/4;
%% 学习速率初始化
u1=0.0015;
u2=0.0015;
u3=0.0015;
u4=0.0015;
u5=0.0015;
%% 权值阀值初始化
t=1;
w11=a;
w21=-y(1,1);
w22=2*b1/a;
w23=2*b2/a;
w24=2*b3/a;
w25=2*b4/a;
w26=2*b5/a;
w31=1+exp(-a*t);
w32=1+exp(-a*t);
w33=1+exp(-a*t);
w34=1+exp(-a*t);
w35=1+exp(-a*t);
w36=1+exp(-a*t);
theta=(1+exp(-a*t))*(b1*y(1,2)/a+b2*y(1,3)/a+b3*y(1,4)/a+b4*y(1,5)/a+b5*y(1,6)/a-y(1,1));
kk=1;
%% 循环迭代
for j=1:10
E(j)=0;
for i=1:30
%% 网络输出计算
t=i;
LB_b=1/(1+exp(-w11*t)); %LB层输出
LC_c1=LB_b*w21; %LC层输出
LC_c2=y(i,2)*LB_b*w22; %LC层输出
LC_c3=y(i,3)*LB_b*w23; %LC层输出
LC_c4=y(i,4)*LB_b*w24; %LC层输出
LC_c5=y(i,5)*LB_b*w25; %LC层输出
LC_c6=y(i,6)*LB_b*w26; %LC层输出
LD_d=w31*LC_c1+w32*LC_c2+w33*LC_c3+w34*LC_c4+w35*LC_c5+w36*LC_c6; %LD层输出
theta=(1+exp(-w11*t))*(w22*y(i,2)/2+w23*y(i,3)/2+w24*y(i,4)/2+w25*y(i,5)/2+w26*y(i,6)/2-y(1,1)); %阀值
ym=LD_d-theta; %网络输出值
yc(i)=ym;
%% 权值修正
error=ym-y(i,1); %计算误差
E(j)=E(j)+abs(error); %误差求和
error1=error*(1+exp(-w11*t)); %计算误差
error2=error*(1+exp(-w11*t)); %计算误差
error3=error*(1+exp(-w11*t));
error4=error*(1+exp(-w11*t));
error5=error*(1+exp(-w11*t));
error6=error*(1+exp(-w11*t));
error7=(1/(1+exp(-w11*t)))*(1-1/(1+exp(-w11*t)))*(w21*error1+w22*error2+w23*error3+w24*error4+w25*error5+w26*error6);
%修改权值
w22=w22-u1*error2*LB_b;
w23=w23-u2*error3*LB_b;
w24=w24-u3*error4*LB_b;
w25=w25-u4*error5*LB_b;
w26=w26-u5*error6*LB_b;
w11=w11+a*t*error7;
end
end
%% 绘制误差随进化次数的变化趋势
figure(1)
plot(E)
title('训练误差','fontsize',12);
xlabel('进化次数','fontsize',12);
ylabel('误差','fontsize',12);
%根据训练的灰色神经网络进行预测
for i=31:36
t=i;
LB_b=1/(1+exp(-w11*t)); %LB层输出
LC_c1=LB_b*w21; %LC层输出
LC_c2=y(i,2)*LB_b*w22; %LC层输出
LC_c3=y(i,3)*LB_b*w23; %LC层输出
LC_c4=y(i,4)*LB_b*w24; %LC层输出
LC_c5=y(i,5)*LB_b*w25;
LC_c6=y(i,6)*LB_b*w26;
LD_d=w31*LC_c1+w32*LC_c2+w33*LC_c3+w34*LC_c4+w35*LC_c5+w36*LC_c6; %LD层输出
theta=(1+exp(-w11*t))*(w22*y(i,2)/2+w23*y(i,3)/2+w24*y(i,4)/2+w25*y(i,5)/2+w26*y(i,6)/2-y(1,1)); %阀值
ym=LD_d-theta; %网络输出值
yc(i)=ym;
end
yc=yc*100000;
y(:,1)=y(:,1)*10000;
%% 计算预测的每月需求量
for j=36:-1:2
ys(j)=(yc(j)-yc(j-1))/10;
end
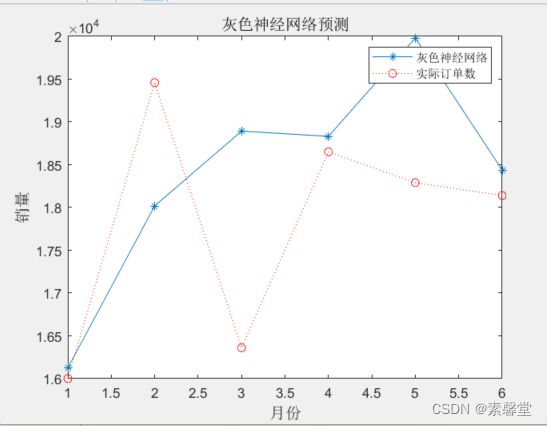
figure(2)
plot(ys(31:36),'-*');
hold on
plot(X(31:36,1)*10000,'r:o');
legend('灰色神经网络','实际订单数')
title('灰色神经网络预测','fontsize',12)
xlabel('月份','fontsize',12)
ylabel('销量','fontsize',12)
3.运行结果