PolarFormer：Multi-camera 3D Object Detection with Polar Transformer——论文笔记

参考代码：PolarFormer

1. 概述

介绍：在仓库RoboBEV中总结了现有的一些bev感知算法在不同输入情况下的鲁棒性，在这些感知算法中PolarFormer拥有较为不错的泛化性能。这个算法的思想是将之前由直角坐标系栅格化构建bev网格，转换到由极坐标构建栅格化bev网格，这样的bev特征构建方法其实是符合相机成像过程的，在W维度切分的单个竖向特征代表的便是由光心和两条射线组成的扇形区域。其大体过程为：首先需要使用transformer机制对各个扇形区域进行特征抽取，而完整的感知区域（一个由车体为中心的圆形区域）则通过双线性插值的方式在各个扇区取值得到，之后会经过self-attention网络完成特征优化，而且fov到bev特征转换的过程会在多个特征尺度上完成，因而这个过程构建的是一个多尺度bev特征，最后的感知头则是类detr的实现。整体上看这个算法从bev特征构建、获取、感知预测简洁明了，但是这样的算法构建要是上车部署估计还有一段路要走。

在RoboBEV中变化不同的输入情况下PolarFormer的退化情况：

2. 方法设计

2.1 整体pipeline

整个bev感知算法的结构见下图所示：

结合上图内容可以将整个算法结构划分为如下几个部分：

• 1）使用backbone+fpn实现图像特征抽取
• 2）以车体为中心对感知范围划分不同的扇区，并以扇区构建query，通过cross-attention的形式得到各个扇区的特征表达
• 3）对各个扇区通过双线性插值得到完整bev特征，在此基础上通过self-attention完成bev特征优化和对齐
• 4）设置需要感知目标的query通过mul-scale deformable attention实现在多尺度特征下的感知

2.2 fov到bev的转换

这篇文章中bev特征的表达和感知都是在极坐标下完成的，因而需要在特征转换的时候也需要直角坐标系到极坐标系的转换，如下图：

对于图像中的点$(x^{(I)},y^{(I)})$，图像视锥坐标系下的点$(x^{(C)},y^{(C)},z^{(C)})$，极坐标系下的点$({\varphi }^P,{\rho }^{(P)})$，它们的转换关系为：
$${\varphi }^{(P)}=arctan\frac{x^{(C)}}{z^{(C)}}=arctan\frac{x^{(I)}-u_0}{f_x}$$
$${\rho }^{(P)}=\sqrt{(x^{(C)}{)}^2+(z^{(C)}{)}^2}=z^{(C)}\sqrt{(\frac{x^{(I)}-u_0}{f_x}{)}^2+1}$$
上面的转换关系会在生成GT的过程中参与到，而在对应特征转换和预测过程中是不会怎么涉及的，这里没有假定扇形区域深度的概念，对于扇形范围的特征为${\hat{p}}_{x,u,w}\in R^{R_u\ast C}$，其中$(x,u,w,R_u)$分别代表camera_id，多尺度特征index，特征的宽度和极坐标的范围（也就是对应的range）。则对应的图像特征为$f_{x,u,w}\in R^{H_u\ast C}$，那么后面就是根据cross-attention实现扇区特征的获取：
$$p_{n,u,w}=MultiHead({\hat{p}}_{n,u,w},f_{x,u,w},f_{x,u,w})$$
上面得到的是一个扇区的特征表达，那么周视的完整bev特征表达就是这些扇区的叠加：
$$p_{n,u}=Stack([p_{n,u,1},\dots ,p_{n,u,w_u}],dim=1)\in R^{R_u\ast W\ast C}$$
按照上面的过程已经得到一个特征scale下的表达，则实际bev极坐标到图像视锥极坐标的转换就需要通过采样的方式实现了，这里也是借鉴了世界坐标到图像坐标的转换，也就是
$$({\varphi }^P,{\rho }^{(P)})=Ca{m}_{I}Ca{m}_E({\varphi }^W,{\rho }^{(W)})$$
然后对这些投影过来的点按照双线性插值的方式获取实际bev极坐标下的特征表达：
$$G_u({\rho }_i^{(P)},{\varphi }_j^P)=\frac{1}{{\sum }_{n=1}^N{\sum }_{n=1}^Z{\lambda }_n({\rho }_i^{(P)},{\varphi }_i^{(P)},z_k^{(P)})}\cdot \sum _{n=1}^N\sum _{n=1}^Z{\lambda }_n({\rho }_i^{(P)},{\varphi }_i^{(P)},z_k^{(P)})\mathcal{B}(P_{n,u},({\bar{x}}_{i,j,k,n}^{(I)},{\bar{r}}_{i,j,n}))$$
上面得到的特征还是比较原始的特征还需要经过几层self-attention网络进行特征优化和对齐操作。那么使用这样的坐标达标具体会有什么样的收益？见下表

而这里的扇形划分分辨率和range对性能的影响：

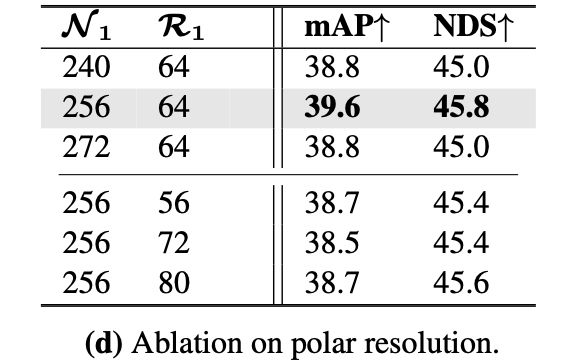
极坐标建模与直角坐标建模在不同距离下的性能差异：

2.3 感知头部分

前面得到的bev特征是多尺度的，则在感知头部分便使用multi-scale deformable attention构建head部分，其结构见下图所示：

对于multi-scale特征给网络性能带来的影响见下表：

3. 实验结果

nuScenes test set：