DAY27：回溯算法（二）组合问题及其优化

77.组合（一定要注意逻辑问题）

• 本题控制起点的搜索方式比较重要，同时一定要注意每层递归中参数的值，可能和我们认为的累加是不一样的！有的参数递归中累加，但是返回到第一层进行回溯的时候，参数值仍然是初始值，这时候就有可能出现重复的逻辑错误！
• 不容易出错的累加方式是在传入参数的时候直接传入经历了for循环的i，用于新的搜索起点

给定两个整数 n 和 k，返回范围 [1, n] 中所有可能的 k 个数的组合。

你可以按 任何顺序 返回答案。

示例1：

输入：n = 4, k = 2
输出：
[
  [2,4],
  [3,4],
  [2,3],
  [1,2],
  [1,3],
  [1,4],
]

示例2

输入：n = 1, k = 1
输出：[[1]]

提示：

• 1 <= n <= 20
• 1 <= k <= n

思路

for循环嵌套的情况

如果我们只考虑n=size大小的数组中取k=2个元素的组合情况，可以用两个for循环来写：

for(int i=0;i<=nums.size();i++){
    for(j=i+1;j<nums.size();i++){
        cout<<nums[i]<<","<<nums[j]<<endl;
    }
}

如果k=2，我们确实可以用两层for循环来解决。

如果k=3，我们可以再加一层for循环，比如：

for(int i=0;i<=nums.size();i++){
    for(j=i+1;j<nums.size();i++){
        for(int k=j+1;k<nums.size();k++){
            cout<<nums[i]<<","<<nums[j]<<","<<nums[k]<<endl;
        }  
    }
}

但是，如果集合更大，k=50的时候，我们不能写50个for循环来寻找这个子集。

也就是说，此时直接的for循环嵌套已经无法实现了。

回溯算法模拟for循环K层嵌套

我们需要使用回溯算法来模拟，实际上回溯算法也是模拟了这样的过程。

回溯算法通过递归来控制有多少层for循环，每一层递归都是一个for循环。

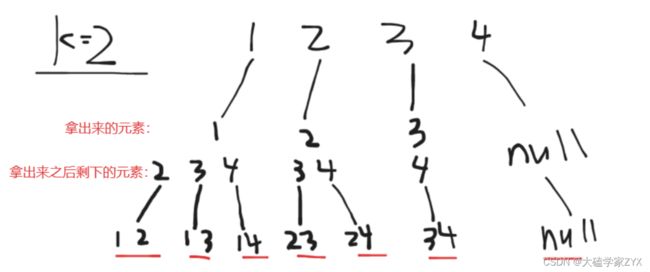
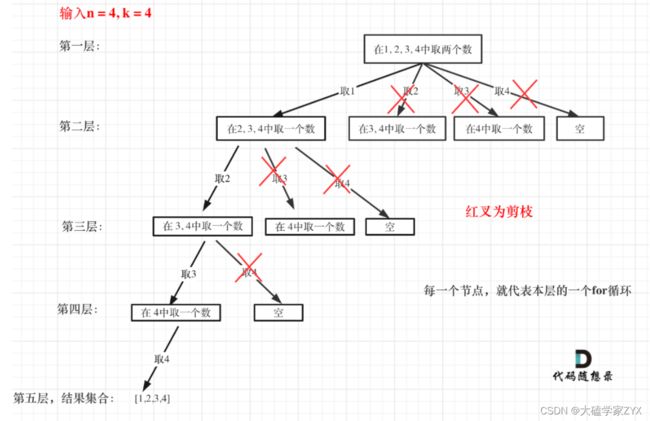
我们画出k=2情况下的树形结构，如图：

可以看出，我们所有的结果都放在叶子节点上。

在2的分支里，我们如果不删掉1，就会多出来2 1这个分支，但是2 1和前面的1 2重复了，因为本题是组合而不是排列。如果是排列的话，子树节点需要留下1。

同时组合的元素不可以有重复，所以子节点的2本身也不能有。

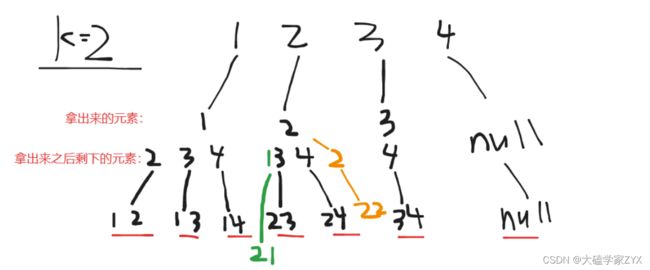
也就是说，我们取2，剩余集合就是2后面的。取3，剩余集合就是3后面的。

为了达到这个效果，我们需要通过每次递归传入startIndex参数，来控制每次搜索的起始位置。

回溯法步骤

• 回溯的第一步，仍然是先确定递归函数的参数和返回值
• 第二步是确定递归的终止条件
• 确定单层搜索的逻辑，单层搜索的逻辑其实就是单层递归的逻辑

伪代码

• 依照树形结构来写，本质上我们求的组合，其实就是一个个路径！求组合的过程就是求路径的过程。
• startIndex控制搜索起点

//参数：一个组合就是一个一维数组path，还需要一个二维数组result来存放组合结果
//这两个参数可以放全局变量也可以不放，参数过多影响可读性可以放全局
//除此之外还需要n和k，还需要startIndex，来控制搜索起点
void backtracking(vector<int>&path,vector<vector<int>>&result,int n,int k,int startIndex){
    //终止条件，找到了大小为K的组合终止
    if(path.size()==k){
        result.push_back(path);
        return;
    }
    //单层递归逻辑，也就是单层搜索逻辑
    //树形结构中每一个节点都是一个for循环，从startIndex开始遍历剩余元素
    //n就是传入集合的大小
    for(i=startIndex;i<=n;i++){
        //path搜索路径上的元素,先把第一个放进来
        path.push_back(i);
        //下一层递归，i+1和startIndex+1？
        backtracking(path,result,n,k,startIndex+1);
        //回溯，把之前的元素pop出去
        //也就是说，取到[1,2]之后就把2弹出！才能继续取3和4！
        path.pop();
    }
    return;
}

完整版

• 因为还需要传入控制搜索起点的参数startIndex，因此我们需要单独写函数来进行回溯。
• 注意传入的数组就是闭区间[1,n]里的所有数字，所以不需要考虑下标问题，因为传入的并不是数组，而是闭区间[1,n]内的所有整数。
• 递归的过程中，重点是需要让for循环不再遍历之前已经遍历过的数字！而当把1pop出去，开始遍历2开头元素的时候，我们一定要注意，startIndex在第一层递归的时候，它的值一直都是1！所以后面遍历每一个不以1开头的都会出问题，因为这一层的startIndex一直都是从2开始找的！

//这里如果用值传递就会没有输出，因为改的是副本，没输出一定要考虑是不是传递错了
void backtracking(vector<int>&path,vector<vector<int>>&result,int n,int k,int startIndex){
    //终止
    if(path.size()==k){
        result.push_back(path);
        return;
    }
    //单层递归
    for(int i = startIndex;i<=n;i++){
        //加入路径
        path.push_back(i);
        //找到i开头的所有组合 12 13 14
        backtracking(path,result,n,k,i+1);
        //回溯,去掉1开始找2开头的，如果传入startIndex+1那么找2开头的就会出问题了
        path.pop();
    }
    return;
}
vector<vector<int>> combine(int n, int k) {
	vector<int>path;
    vector<vector<int>>result;
    int startIndex = 1;
    backtracking(path,result,n,k,startIndex);
    return result;
}

debug测试

• 注意结果集一定要用引用传递！

逻辑问题：没有输出

传入数组的时候用了值传递，值传递只会修改副本！

如果使用了值传递，当 backtracking 函数返回时，任何对 result 的修改都不会影响到函数外部的 result，也就不会影响到最终的结果。也就是说主函数的result仍然是空的，所以输出为空。

应将result改为引用传递。

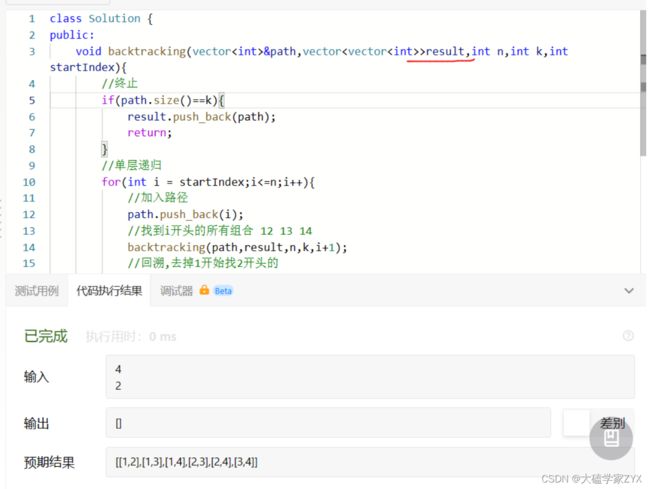
逻辑问题：为什么是递归传入i+1而不是startIndex+1？

如果递归参数引用写成了startIndex+1，那么会导致以下输出：

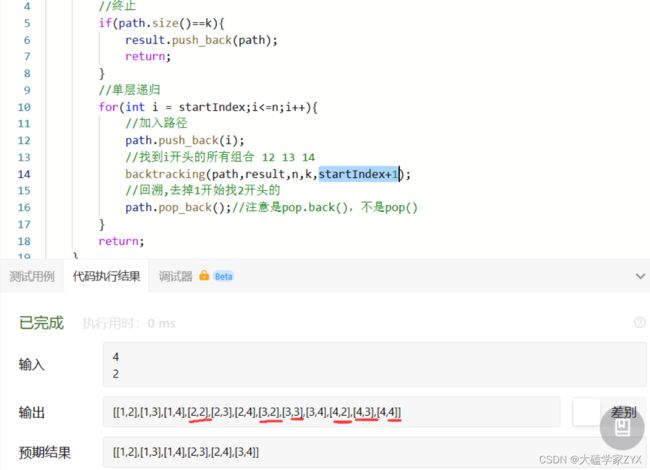
我们会发现多输出了几个结果，包括[2,2],[3,2],[3,3],[4,2],[4,3],[4,4]。

重要：为什么会输出[2,2],[3,2],[4,2]？

因为递归的过程中，重点是需要让for循环不再遍历之前已经遍历过的数字！而当回到第一层递归，把1pop出去，开始遍历2开头元素的时候，我们一定要注意，startIndex在第一层递归的时候，它的值一直都是1！所以后面遍历每一个不以1开头的都会出问题，因为这一层的startIndex一直都是从2开始找的！

所以，才会出现[2,2],[3,2],[4,2]这样的结果，因为返回第一层递归开始确认下一个元素的时候，startIndex的值是这一层递归的值！也就是第一层递归startIndex一直=1！！

注意startIndex这种用法

startIndex并不是通过本身的值改变来控制搜索起点！startIndex是一个为了改变for循环初始值设定的参数！每一次递归都会更新startIndex，为了让for循环能够跳过已经包含过的元素，从新的位置开始！

当startIndex这个参数被赋值为i+1的时候，我们就相当于控制了for(i=startIndex,i这个循环的起点！只要我们每次令startIndex=i+1再传入递归之中，我们就可以保证结果中不再存在已经在前面的for循环中处理过的数字，比如输第一位是2的时候2的下一位不会是2本身！

特别注意：

虽然 直接传入startIndex+1看似也能完成这个效果，但是只能在递归第一个元素的时候完成 ！只有当我们传入第一个元素的时候，才能保证第一个元素后面跟着的元素和第一个本身不同。但是，当我们把第一个元素pop出去，开始搜索第二个元素为首位的组合时，startIndex还保留了递归第一层的时候的那个初始值，也就是1，那么此时还是会遍历第二个元素！因为第一层的startIndex的初值并没有变化！

每一层递归都有它自己的 startIndex 值，而这个值在这一层递归中是不会改变的。因此，当我们在递归调用中使用 startIndex+1 时，实际上是在使用当前递归级别的起始索引加一，而不是 path 中最后一个元素的下一个值。

所以，当我们想要调用path 中最后一个元素的下一个值的时候，我们一定要用i+1，而不是startIndex+1。这就是我的逻辑错误，从第二个元素开始输出重复组合的原因。

77.组合（剪枝优化）

回溯法虽然是暴力搜索，但是有时候也是可以剪枝优化的。

• 剪枝优化的重点就在于，如果剩下的元素小于还需要被拿出的元素，那么就可以结束循环了。
• 当我们无法一下子列出关于i的结束条件，我们可以考虑先列式再左右移项！

剪枝思路：

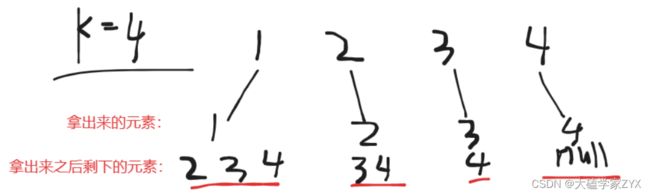
例子：n=4, k=4 时候的情况

当我们取2的时候，剩余的元素是3和4，此时一共就只有3个元素，怎么搜也不可能搜到path.size()==k的情况了。

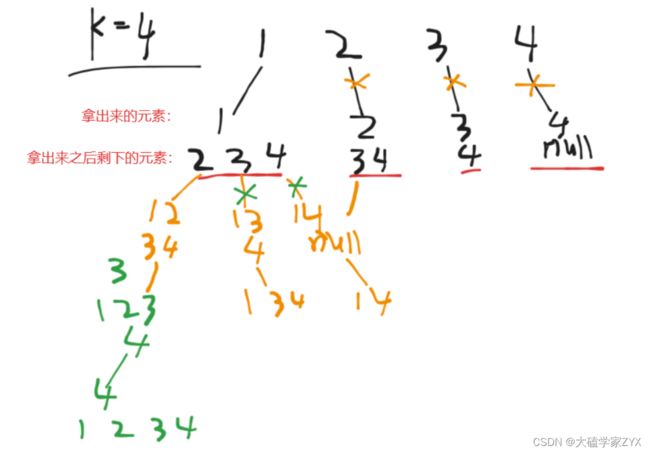
这个情况就可以做剪枝，也就是如下图所示的情况

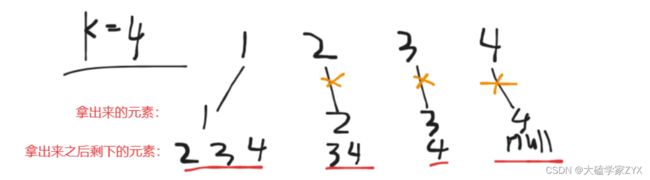
因为剪枝剪掉的是有深度的分支，所以说节省了一部分时间开销。递归深度的示例如下图所示：

如果没有做剪枝的话，回溯算法会搜索整个树形结构。

完整的树形结构 via代码随想录：

伪代码

• 剪枝优化，优化的是单层搜索的逻辑，只修改单层搜索代码即可
• 树形图的每一个节点都是for循环的一个过程

原本的单层递归

void backtracking(int startIndex,int n,int k){
    //直接开始写单层递归
    for(i=startIndex;i<=n;i++){
        path.push_back(i);
        backtracking(i+1,n,k);
        path.pop_back();
    }
}

在原来的递归中，遍历了所有的子孩子，但是实际上可以不遍历这么多的子节点，比如上图的情况，234都不需要遍历。

因此如果要做剪枝，我们就需要在循环结束条件i<=n这里做文章。

剪枝的情况是n=4, k=4，取出第一个元素1之后，再取2，后面剩下的需要被选取的元素就不够了。path是已经被选取的元素个数，还剩下需要被选取的元素个数是k-path.size()，得到我们还需要选取的元素个数。

之后，我们需要计算，元素选取至多从哪个位置开始。至多是指，例如n=4, k=3，那么至多从2开始选取元素，再往后就不可能再有符合要求的了。也就是说，我们需要计算剩余可选的元素的上限索引。

列式计算循环终止条件

n是总的元素数量，k是目标组合的长度，path.size()是当前已经选择的元素数量。 (k - path.size()) 就是还需要选择的元素数量。如果剩余的元素数量，从i到n的元素，也就是n-i+1<(k - path.size())，也就是小于还需要选择的元素数量，那么就不可能再构建出长度为k的组合了。

因此，我们得到的终止条件就是n-i+1<(k - path.size())，也就是i>n-(k-path.size())+1是不满足条件的。所以终止条件应该改成：

i<=n-(k-path.size())+1。

当我们很难一下子得到i的循环终止条件的时候，可以尝试先列式子再左右移项！

优化之后的for循环：

for (int i = startIndex; i <= n - (k - path.size()) + 1; i++) // i为本次搜索的起始位置

优化后的完整版

void backtracking(vector<int>&path,vector<vector<int>>result,int n,int k,int startIndex){
    //终止
    if(path.size()==k){
        result.push_back(path);
        return;
    }
    //单层递归
    for(int i = startIndex;i<=n - (k - path.size()) + 1;i++){
        //加入路径
        path.push_back(i);
        //找到i开头的所有组合 12 13 14
        backtracking(path,result,n,k,i+1);
        //回溯,去掉1开始找2开头的，如果传入startIndex+1那么找2开头的就会出问题了
        path.pop();
    }
    return;
}
vector<vector<int>> combine(int n, int k) {
	vector<int>path;
    vector<vector<int>>result;
    int startIndex = 1;
    backtracking(path,result,n,k,startIndex);
    return result;
}

这种剪枝操作节省了多少时间复杂度？

在没有剪枝的版本中，递归会遍历所有可能的路径。在有剪枝的版本中，当知道某条路径不可能达到目标时，就会停止沿这条路径的搜索，转而搜索其他可能的路径。也就是说，如果当前的路径长度已经达到k，就不必再继续搜索。如果还需要选择的元素数量超过剩余元素数量，也不必继续搜索。这就是剪枝。

从时间复杂度的角度来看，剪枝并不能降低算法的时间复杂度！回溯法的时间复杂度是O(n!)，这是因为需要遍历所有可能的路径。尽管剪枝可以减少搜索的路径数量，但不会改变时间复杂度的数量级，所以时间复杂度仍然是O(n!)。

但是，剪枝可以显著减少实际运行时间和空间开销。因为剪枝可以避免搜索那些明显无法达到目标的路径，因此可以大大减少搜索的路径数量，从而减少计算量。具体节省了多少开销，要根据输入的具体情况来判断，比如n和k的具体值，以及剪枝策略的有效性等。

剪枝操作终止条件计算思路

如果我们不能立即得出循环终止条件，可以通过列出所有相关因素的数学关系来解决。

比如在这个例子中，需要确保剩余的元素足够多，以便构建长度为k的组合。然后，可以将这个逻辑关系式表示为数学式子：

需要的元素数量 <= 剩余的元素数量

即可得到：(k - path.size()) <= n - i + 1

然后解这个式子，再得到i的范围。通过这种方式，我们可以从问题的逻辑关系中得出终止条件剪枝的具体实现。这是一个非常有效的问题解决方法。