北京大学计算机视觉导论23spring Homework1

1.Convolution operation

这个板块需要我们实现一些卷积的操作。

a) Implementing Padding Function

该任务让我们手写两个填充函数。

zero padding

就是边界全部用0来填充。

replication padding

举个例子：

思路是利用数组的切片和numpy的广播来照样子填就行了。

我是先填了红色的这四个角，再填了蓝色的这四条边。

def padding(img, padding_size, type):
    """
        The function you need to implement for Q1 a).
        Inputs:
            img: array(float)
            padding_size: int
            type: str, zeroPadding/replicatePadding
        Outputs:
            padding_img: array(float)
    """

    if type=="zeroPadding":
        h, w = img.shape
        padding_img = np.zeros((h + padding_size*2, w + padding_size*2))
        padding_img[padding_size : padding_size + h, padding_size : padding_size + w] = img
        return padding_img
    elif type=="replicatePadding":
        h, w = img.shape
        padding_img = np.zeros((h + padding_size*2, w + padding_size*2))
        padding_img[padding_size : padding_size + h, padding_size : padding_size + w] = img
        #填充四个角
        padding_img[:padding_size, : padding_size] = img[0][0]
        padding_img[:padding_size, w + padding_size : w + padding_size*2] = img[0][w-1]
        padding_img[h + padding_size : h + padding_size*2, : padding_size] = img[h-1][0]
        padding_img[h + padding_size : h + padding_size*2,w + padding_size : w + padding_size*2] = img[h-1][w-1]
        #填充四个边
        padding_img[ : padding_size, padding_size : padding_size + w] = img[:1,:]
        padding_img[h + padding_size : , padding_size : padding_size + w] = img[-1:,:]
        padding_img[padding_size : h + padding_size,  : padding_size] = img[:,:1]
        padding_img[padding_size : h + padding_size, w + padding_size : w + padding_size*2] = img[:,-1:]
        
        return padding_img

b) Implementing 2D Convolution via Toeplitz Matrix

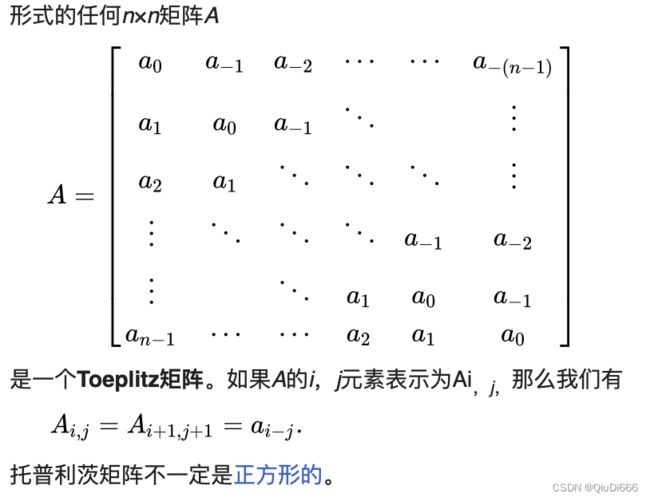
Toeplitz矩阵https://en.wikipedia.org/wiki/Toeplitz_matrix#Discrete_convolution

即对角线常量矩阵

例如，以下矩阵是Toeplitz矩阵：

 

利用Toeplitz矩阵，我们可以把卷积操作转换为矩阵乘操作。

本题是让我们构造一个Toeplitz矩阵来完成卷积操作。

下面是一维卷积的例子

在使用Toeplitz矩阵进行卷积时，我们将图像矩阵展开成一个长向量，然后将卷积核展开成一个Toeplitz矩阵。我们可以将这个Toeplitz矩阵与展开后的图像向量相乘，然后将得到的结果重新排列成输出图像的形状。这个过程可以通过矩阵乘法来实现，因此可以非常高效地进行计算。

参考：

neural network - 2-D convolution as a matrix-matrix multiplication - Stack Overflow

GitHub - alisaaalehi/convolution_as_multiplication: Step by step explanation of 2D convolution implemented as matrix multiplication using toeplitz matrices

 

def convol_with_Toeplitz_matrix(img, kernel):
    """
        The function you need to implement for Q1 b).
        Inputs:
            img: array(float) 6*6
            kernel: array(float) 3*3
        Outputs:
            output: array(float)
    """
    #zero padding
    padding_img = padding(img,1,"zeroPadding") #padding为1时，卷后size不变 padding_img是8*8

    #build the Toeplitz matrix and compute convolution
    I = img
    F = kernel

    # number columns and rows of the input 
    I_row_num, I_col_num = I.shape 

    # number of columns and rows of the filter
    F_row_num, F_col_num = F.shape

    #  calculate the output dimensions
    output_row_num = I_row_num + F_row_num - 1
    output_col_num = I_col_num + F_col_num - 1
    #print('output dimension:', output_row_num, output_col_num)

    # zero pad the filter
    F_zero_padded = np.pad(F, ((output_row_num - F_row_num, 0),
                            (0, output_col_num - F_col_num)),
                            'constant', constant_values=0)
    #print('F_zero_padded: ', F_zero_padded)

    from scipy.linalg import toeplitz

    # use each row of the zero-padded F to creat a toeplitz matrix. 
    #  Number of columns in this matrices are same as numbe of columns of input signal
    toeplitz_list = []
    for i in range(F_zero_padded.shape[0]-1, -1, -1): # iterate from last row to the first row
        c = F_zero_padded[i, :] # i th row of the F 
        r = np.r_[c[0], np.zeros(I_col_num-1)] # first row for the toeplitz fuction should be defined otherwise
                                                            # the result is wrong
        toeplitz_m = toeplitz(c,r) # this function is in scipy.linalg library
        toeplitz_list.append(toeplitz_m)
        #print('F '+ str(i)+'\n', toeplitz_m)

    # doubly blocked toeplitz indices: 
    #  this matrix defines which toeplitz matrix from toeplitz_list goes to which part of the doubly blocked
    c = range(1, F_zero_padded.shape[0]+1)
    r = np.r_[c[0], np.zeros(I_row_num-1, dtype=int)]
    doubly_indices = toeplitz(c, r)
    #print('doubly indices \n', doubly_indices)


    ## creat doubly blocked matrix with zero values
    toeplitz_shape = toeplitz_list[0].shape # shape of one toeplitz matrix
    h = toeplitz_shape[0]*doubly_indices.shape[0]
    w = toeplitz_shape[1]*doubly_indices.shape[1]
    doubly_blocked_shape = [h, w]
    doubly_blocked = np.zeros(doubly_blocked_shape)

    # tile toeplitz matrices for each row in the doubly blocked matrix
    b_h, b_w = toeplitz_shape # hight and withs of each block
    for i in range(doubly_indices.shape[0]):
        for j in range(doubly_indices.shape[1]):
            start_i = i * b_h
            start_j = j * b_w
            end_i = start_i + b_h
            end_j = start_j + b_w
            doubly_blocked[start_i: end_i, start_j:end_j] = toeplitz_list[doubly_indices[i,j]-1]

    #print('doubly_blocked: ', doubly_blocked)
    
    def matrix_to_vector(input):
        input_h, input_w = input.shape
        output_vector = np.zeros(input_h*input_w, dtype=input.dtype)
        # flip the input matrix up-down because last row should go first
        input = np.flipud(input) 
        for i,row in enumerate(input):
            st = i*input_w
            nd = st + input_w
            output_vector[st:nd] = row
        return output_vector

    # call the function
    vectorized_I = matrix_to_vector(I)
    #print('vectorized_I: ', vectorized_I)

    # get result of the convolution by matrix mupltiplication
    result_vector = np.matmul(doubly_blocked, vectorized_I)
    #print('result_vector: ', result_vector)
            
    def vector_to_matrix(input, output_shape):
        output_h, output_w = output_shape
        output = np.zeros(output_shape, dtype=input.dtype)
        for i in range(output_h):
            st = i*output_w
            nd = st + output_w
            output[i, :] = input[st:nd]
        # flip the output matrix up-down to get correct result
        output=np.flipud(output)
        return output
    
    # reshape the raw rsult to desired matrix form
    out_shape = [output_row_num, output_col_num]
    my_output = vector_to_matrix(result_vector, out_shape) #8x8

    #print('Result of implemented method: \n', my_output)

    
    #lib_output = signal.convolve2d(padding_img, F, "valid")
    #np.savetxt("result/lib_result.txt", lib_output)

    output = my_output[1:-1,1:-1] #6x6
    return output

c) Convolution by Sliding Window

        用Toeplitz矩阵实现卷积可以完全并行，但需要构建一个高度稀疏的Toeplitz矩阵（大小近似为N^2 × N^2），对于大小为N × N的图像。另一种实现卷积的替代方法是通过滑动窗口，在每个窗口内简单地计算图像值和内核之间的点积。在本题中，我们需要实现一个卷积运算符，它可以接受任意形状的2D图像作为输入，并使用k × k卷积核进行卷积。在实现此卷积运算符时，可以假设没有填充。

cs231n的笔记 

先写了一个带for循环的理清一下思路

def convolve(img, kernel):
    """
        The function you need to implement for Q1 c).
        Inputs:
            img: array(float)
            kernel: array(float)
        Outputs:
            output: array(float)
    """
    
    #build the sliding-window convolution here
    h, w = img.shape
    k = kernel.shape[0]
    #构造一个(h-k+1)*(w-k+1) x k^2的矩阵 和把kernel拉成k^2 x 1的向量 最后展平成(h-k+1)x(w-k+1)的结果
    kernel_flat = kernel.flatten() 

    output_h = h-k+1
    output_w = w-k+1
    patch_matrix = np.zeros((output_h*output_w,k**2))
    #每一行都是一个kxk的位置的展开 按kernel会卷到的位置把它填上
    for i, j in np.ndindex((output_h, output_w)):
        patch_matrix[i * output_w + j] = img[i:i+k, j:j+k].ravel()

    output_flat = np.dot(patch_matrix, kernel_flat)
    output = output_flat.reshape(output_h, output_w)
    return output

再用np.meshgrid把中间带有for循环的位置给改掉

def convolve(img, kernel):
    """
        The function you need to implement for Q1 c).
        Inputs:
            img: array(float)
            kernel: array(float)
        Outputs:
            output: array(float)
    """
    
    #build the sliding-window convolution here
    h, w = img.shape
    k = kernel.shape[0]
    #构造一个(h-k+1)*(w-k+1) x k^2的矩阵 和把kernel拉成k^2 x 1的向量 最后展平成(h-k+1)x(w-k+1)的结果
    kernel_flat = kernel.flatten() 

    output_h = h-k+1
    output_w = w-k+1
    patch_matrix = np.zeros((output_h*output_w,k**2))
    #每一行都是一个kxk的位置的展开 按kernel会卷到的位置把它填上
    #for i, j in np.ndindex((output_h, output_w)):
    #   patch_matrix[i * output_w + j] = img[i:i+k, j:j+k].ravel()

    rows, cols = np.meshgrid(np.arange(output_h),np.arange(output_w),indexing='ij')
    a,b = np.meshgrid(np.arange(k),np.arange(k),indexing='ij')

    patch_matrix = img[rows[:,:,np.newaxis,np.newaxis] + a[:,:],cols[:,:,np.newaxis,np.newaxis] + b[:,:]]
    patch_matrix = patch_matrix.reshape(output_h*output_w,-1)
    
    output_flat = np.dot(patch_matrix, kernel_flat)
    output = output_flat.reshape(output_h, output_w)
    return output

在 img[rows[:,:,np.newaxis,np.newaxis] + a[:,:],cols[:,:,np.newaxis,np.newaxis] + b[:,:]]中，每个坐标 (i, j) 都会生成一个大小为 (k, k) 的矩阵，因此最终输出的大小应该是 (output_h, output_w, k, k)。

在这个例子中，img是6x6，output_h = output_w = 4，k = 3，因此最终输出的大小是 (4, 4, 3, 3)。其中，第一个维度和第二个维度分别对应着每个输出像素的坐标，第三个维度和第四个维度则是每个像素对应的卷积核的值。

d) Gaussian Filter

高斯滤波可以消除噪声，直观来看就是让图像变模糊。

这个任务不用我们写，我们就来阅读学习一下。

def Gaussian_filter(img):
    padding_img = padding(img, 1, "replicatePadding")
    gaussian_kernel = np.array([[1/16,1/8,1/16],[1/8,1/4,1/8],[1/16,1/8,1/16]])
    output = convolve(padding_img, gaussian_kernel)
    return output

blur

e) Sobel Filter

索贝尔算子主要用于获得数字图像的一阶梯度，常用于边缘检测。

索贝尔算子是把图像中每个像素的上下左右四领域的灰度值加权差，在边缘处达到极值从而检测边缘。

Sobel 算子有两个，一个是检测水平边缘的 ；另一个是检测垂直边缘的。

与Prewitt算子相比，Sobel算子对于象素的位置的影响做了加权，可以降低边缘模糊程度，因此效果更好。

这个任务也不用我们写，就来读代码学习一下。

def Sobel_filter_x(img):
    padding_img = padding(img, 1, "replicatePadding")
    sobel_kernel_x = np.array([[-1,0,1],[-2,0,2],[-1,0,1]])
    output = convolve(padding_img, sobel_kernel_x)
    return output

def Sobel_filter_y(img):
    padding_img = padding(img, 1, "replicatePadding")
    sobel_kernel_y = np.array([[-1,-2,-1],[0,0,0],[1,2,1]])
    output = convolve(padding_img, sobel_kernel_y)
    return output

grad_x

grad_y

2.Canny Edge Detector

写一个Canny edge detector，完成其中的3个关键函数。

a）Compute the Image Gradient.

 我们来看一下Canny边缘检测的步骤：

1.高斯滤波减少噪声。

由于图像边缘非常容易受到噪声的干扰，为了避免检测到错误的边缘信息，通常需要对图像进行滤波以除去噪声。滤波的目的是平滑一些纹理较弱的非边缘区域，以便得到更准确的边缘。

2.计算梯度

 3.非极大抑制

在边缘检测过程中，我们通常使用梯度信息来确定图像中的边缘。在获取梯度幅值和方向之后，我们需要进一步处理这些信息来确定哪些像素构成了边缘。

然而，由于图像中存在许多边缘，我们需要从中选择最显著的边缘。非极大值抑制（NMS）是一种常用的技术，它可以找到梯度方向上的局部最大值，并将其视为边缘的一部分。这是因为在边缘处，像素值变化最大，而梯度也最大。因此，在梯度方向上选择局部最大值可以帮助我们确定哪些像素构成了边缘。

在具体实现时，逐一遍历像素点，判断当前像素点是否是周围像素点中具有相同梯度方向的最大值，并根据判断结果决定是否抑制该点。

简化为4个方向：—、｜、/、\ 

比如说黄色这个方向上的线，可能会有很粗的线（红色）都是边缘，所以检查，挑大的。

4.应用双阈值确定边缘

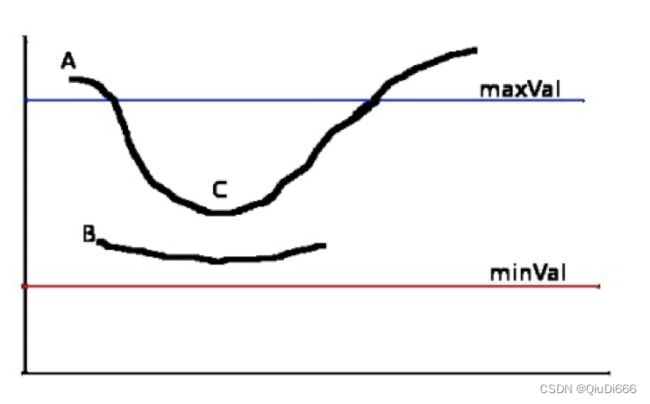
分别为高阀值(maxVal)和低阀值(minVal)。根据当前边缘像素的梯度幅度与这两个阀值之间的关系，判断边缘的属性，具体步骤如下:
   ①如果当前边缘像素的梯度幅度大于或等于高阀值，则将当前边缘像素标记为强边缘（需要保留）。
  ②如果当前边缘像素的梯度幅度介于高阀值与低阀值之间，则将当前边缘像素标记为虚边缘（需要保留）。
  ③如果当前边缘像素的梯度幅度小于或等于低阀值，则抑制当前边缘像素（需要抛弃）。

 在上述过程中我们得到了虚边缘，需要对其做进一步处理。一般通过判断虚边缘和强边缘是否连接来确定虚边缘到底属于哪种情况。通常情况下，对于一个虚边缘：
  ①与强边缘连接，则将该边缘处理为边缘。
  ②与强边缘无连接，则该边缘为弱边缘，将其抑制。

Canny边缘检测_半濠春水的博客-CSDN博客

 完整代码如下：

import numpy as np
from HM1_Convolve import Gaussian_filter, Sobel_filter_x, Sobel_filter_y
from utils import read_img, write_img
import math
def compute_gradient_magnitude_direction(x_grad, y_grad):
    """
        The function you need to implement for Q2 a).
        Inputs:
            x_grad: array(float) 
            y_grad: array(float)
        Outputs:
            magnitude_grad: array(float)
            direction_grad: array(float) you may keep the angle of the gradient at each pixel
    """
    magnitude_grad = np.sqrt(x_grad**2 + y_grad**2)
    direction_grad = np.arctan2(y_grad,x_grad)*(180/np.pi) #arctan2 return [-pi,pi]
    direction_grad[direction_grad<0] += 180 # 范围0-180
    #simply to 4 directions
    direction_grad[(0<=direction_grad) & (direction_grad<22.5)] = 0
    direction_grad[(22.5<=direction_grad) & (direction_grad<67.5)] = 45
    direction_grad[(67.5<=direction_grad) & (direction_grad<112.5)] = 90
    direction_grad[(112.5<=direction_grad) & (direction_grad<157.5)] = 135
    direction_grad[(157.5<=direction_grad) & (direction_grad<=180)] = 0
    
    write_img("result/mag.png", magnitude_grad*255)
    write_img("result/dir.png", direction_grad*255)

    return magnitude_grad, direction_grad 



def non_maximal_suppressor(grad_mag, grad_dir):
    """
        The function you need to implement for Q2 b).
        Inputs:
            grad_mag: array(float) 
            grad_dir: array(float)
        Outputs:
            output: array(float)
    """   
    NMS_output = np.copy(grad_mag)

    NMS_output[(abs(grad_dir - 0) < 1e-6) \
                   & ((np.roll(grad_mag, shift=1, axis=1)>grad_mag) \
                        | (np.roll(grad_mag, shift=-1, axis=1)>grad_mag))] = 0
    #write_img("result/NMS_mag1.png", NMS_output*255)

    NMS_output[(abs(grad_dir - 90) < 1e-6) \
                   & ((np.roll(grad_mag, shift=1, axis=0)>grad_mag )
                        | (np.roll(grad_mag, shift=-1, axis=0)>grad_mag))] = 0
    #write_img("result/NMS_mag2.png", NMS_output*255)
    NMS_output[(abs(grad_dir - 45) < 1e-6) \
                   & ((np.roll(np.roll(grad_mag, shift=1, axis=1), shift=1, axis=0)>grad_mag )\
                        | (np.roll(np.roll(grad_mag, shift=-1, axis=1), shift=-1, axis=0)>grad_mag))] = 0
    #write_img("result/NMS_mag3.png", NMS_output*255)
    NMS_output[(abs(grad_dir - 135) < 1e-6) \
                   & ((np.roll(np.roll(grad_mag, shift=-1, axis=0), shift=1, axis=1)>grad_mag )\
                        | (np.roll(np.roll(grad_mag, shift=1, axis=0), shift=-1, axis=1)>grad_mag))] = 0
    
    #write_img("result/NMS_mag.png", NMS_output*255)

    return NMS_output 
            


def hysteresis_thresholding(img) :
    """
        The function you need to implement for Q2 c).
        Inputs:
            img: array(float) 
        Outputs:
            output: array(float)
    """
    #you can adjust the parameters to fit your own implementation 
    low_ratio = 0.10
    high_ratio = 0.30
    
    judge = np.zeros_like(img) #高于max 1 低于min -1 介于两者之间 0
    judge[img>high_ratio] = 1
    judge[img0)] = 1 

        num_nxt = np.count_nonzero(judge)
        if num_cnt == num_nxt:
            break
        num_cnt = num_nxt

    output = np.where(abs(judge-1)<1e-6,1,0)
    return output 



if __name__=="__main__":

    #Load the input images
    input_img = read_img("lenna.png")/255

    #Apply gaussian blurring
    blur_img = Gaussian_filter(input_img)

    x_grad = Sobel_filter_x(blur_img)
    y_grad = Sobel_filter_y(blur_img)

    #Compute the magnitude and the direction of gradient
    magnitude_grad, direction_grad = compute_gradient_magnitude_direction(x_grad, y_grad)

    #NMS
    NMS_output = non_maximal_suppressor(magnitude_grad, direction_grad)

    #Edge linking with hysteresis
    output_img = hysteresis_thresholding(NMS_output)
    
    write_img("result/HM1_Canny_result.png", output_img*255)

输出结果如下：

 不能说和标答一模一样，但可以说是差强人意。

3.Harris Corner Detector

图像处理基础（七）Harris 角点检测 - 知乎

https://www.cnblogs.com/klitech/p/5779600.html

还是先写一个简单一点带for循环的来理一下思路

def corner_response_function(input_img, window_size, alpha, threshold):
    """
        The function you need to implement for Q3.
        Inputs:
            input_img: array(float)
            window_size: int
            alpha: float
            threshold: float
        Outputs:
            corner_list: list
    """

    # please solve the corner_response_function of each window,
    # and keep windows with theta > threshold.
    # you can use several functions from HM1_Convolve to get 
    # I_xx, I_yy, I_xy as well as the convolution result.
    # for details of corner_response_function, please refer to the slides.

    corner_list = []
    #计算两个方向的梯度
    x_grad = Sobel_filter_x(input_img)
    y_grad = Sobel_filter_y(input_img)

    xx_matrix = np.multiply(x_grad,x_grad)
    yy_matrix = np.multiply(y_grad,y_grad)
    xy_matrix = np.multiply(x_grad,y_grad)

    h, w = input_img.shape
    #做滤波 这里直接用长方形的 即均值滤波 1 in window 0 outside
    # 不同的局部窗口会得到不同的M矩阵

    for i in range(h):
        for j in range(w):
            xx_sum = xx_matrix[i:i+window_size,j:j+window_size].sum() 
            xy_sum = xy_matrix[i:i+window_size,j:j+window_size].sum()
            yy_sum = yy_matrix[i:i+window_size,j:j+window_size].sum()
            M = np.array([[xx_sum, xy_sum],
                          [xy_sum, yy_sum ]])
            #角点响应值R = detM - alphax(traceM)^2  alpha是一个常数 一般在0.04~0.06 这里给的是0.04
            theta = np.linalg.det(M)- alpha*(np.trace(M))**2
            if theta > threshold:
                corner_list.append((i+1,j+1,theta))

    return corner_list # the corners in corne_list: a tuple of (index of rows, index of cols, theta)

输入结果如下：

 看起来没有什么太大问题，下面我们再来把for循环给去掉

def corner_response_function(input_img, window_size, alpha, threshold):
    """
        The function you need to implement for Q3.
        Inputs:
            input_img: array(float)
            window_size: int
            alpha: float
            threshold: float
        Outputs:
            corner_list: list
    """

    # please solve the corner_response_function of each window,
    # and keep windows with theta > threshold.
    # you can use several functions from HM1_Convolve to get 
    # I_xx, I_yy, I_xy as well as the convolution result.
    # for details of corner_response_function, please refer to the slides.

    corner_list = []
    #计算两个方向的梯度
    x_grad = Sobel_filter_x(input_img)
    y_grad = Sobel_filter_y(input_img)

    xx_matrix = np.multiply(x_grad,x_grad)
    yy_matrix = np.multiply(y_grad,y_grad)
    xy_matrix = np.multiply(x_grad,y_grad)

    h, w = input_img.shape
    #做滤波 这里直接用长方形的 即均值滤波 1 in window 0 outside
    # 不同的局部窗口会得到不同的M矩阵

    #用来在窗口内遍历 window_size=5时 arange是(-2,3) 也就是-2 -1 0 1 2 
    '''
    for i in range(h):
        for j in range(w):
            xx_sum = xx_matrix[i:i+window_size,j:j+window_size].sum() 
            xy_sum = xy_matrix[i:i+window_size,j:j+window_size].sum()
            yy_sum = yy_matrix[i:i+window_size,j:j+window_size].sum()
            M = np.array([[xx_sum, xy_sum],
                          [xy_sum, yy_sum ]])
            #角点响应值R = detM - alphax(traceM)^2  alpha是一个常数 一般在0.04~0.06 这里给的是0.04
            theta = np.linalg.det(M)- alpha*(np.trace(M))**2
            if theta > threshold:
                corner_list.append((i+1,j+1,theta))'''
    
    window_kernel = np.ones((5,5))
    #xx_sum_matrix（i，j）的值表示上面for循环里的xx_sum
    xx_sum_matrix = convolve(padding(xx_matrix,2,"replicatePadding"), window_kernel)
    xy_sum_matrix = convolve(padding(xy_matrix,2,"replicatePadding"), window_kernel)
    yy_sum_matrix = convolve(padding(yy_matrix,2,"replicatePadding"), window_kernel)

    M = np.stack((np.stack((xx_sum_matrix, xy_sum_matrix), axis=-1), np.stack((xy_sum_matrix, yy_sum_matrix), axis=-1)), axis=-2)
    #每个点处的响应值theta
    theta = np.linalg.det(M) - alpha * (np.trace(M, axis1=-2, axis2=-1)**2)

    # 将符合条件的角点加入列表中
    i, j = np.where(theta > threshold)
    corner_list = list(zip(i, j, theta[i,j]))

    return corner_list # the corners in corne_list: a tuple of (index of rows, index of cols, theta)

4.基于RANSAC的平面拟合

用RANSAC来写一个Plane Fitting（平面拟合）算法。

在平面拟合过程中，RANSAC算法会随机选择一组数据点，并根据这些点估计平面模型的参数。然后，算法会计算所有数据点到该平面的距离，并将距离小于某个阈值的数据点视为该平面的内点。在一定数量的迭代后，算法会选择具有最多内点的平面模型作为最终的拟合结果。

分为3个步骤：

1. hypothesis generation

在假设生成过程中，需要随机选择一组种子点，并根据这些点估计平面参数，生成一个假设。需要确定生成的假设数量，以使得至少有一个假设在99.9％的概率下不包含任何异常值。并且需要使用并行计算的技术，同时生成所有的假设。

2. verification

计算内点（inlier）的数量。

3.final refinement

在RANSAC算法中，需要从所有生成的假设中选择具有最多内点的假设作为最佳假设。内点是指与平面模型匹配良好的数据点。选出最佳假设后，需要利用它的内点使用最小二乘法来估计最终平面参数，最小二乘法会最小化数据点到平面的垂直距离的平方和。最终得到的平面模型即为所求的平面拟合结果。

import numpy as np
from utils import draw_save_plane_with_points


def get_plane(points):
    p1 = points[:, 0]
    p2 = points[:, 1]
    p3 = points[:, 2]
    a = ( (p2[:,1]-p1[:,1])*(p3[:,2]-p1[:,2])-(p2[:,2]-p1[:,2])*(p3[:,1]-p1[:,1]) )
    b = ( (p2[:,2]-p1[:,2])*(p3[:,0]-p1[:,0])-(p2[:,0]-p1[:,0])*(p3[:,2]-p1[:,2]) )
    c = ( (p2[:,0]-p1[:,0])*(p3[:,1]-p1[:,1])-(p2[:,1]-p1[:,1])*(p3[:,0]-p1[:,0]) )
    d = ( 0-(a*p1[:,0]+b*p1[:,1]+c*p1[:,2]) )
    return np.stack([a, b, c, d], axis=-1)


def is_inliers(p,para,threshold): #para (sample_time, 4) 该函数表示一个点对于这sample_time种情况来说是否是内点 返回(sample_time,)大小
    A = para[:,0] #(sample_time,)
    B = para[:,1]
    C = para[:,2]
    D = para[:,3]
    num1 = A*p[0] + B*p[1] + C*p[2] + D #(sample_time,)
    num2 = np.sqrt(np.sum(np.square([A, B, C]),axis=0))  #(sample_time,)
    dis = np.abs(num1)/num2  #(sample_time,1)
    judge_inliers = np.zeros_like(dis) #(sample_time,)
    judge_inliers[dis0.999 解出来大概11.几 这里保证概率 向上取到15 反正向量化跑起来很快
    sample_time = 15 #more than 99.9% probability at least one hypothesis does not contain any outliers 
    distance_threshold = 0.05

    # sample points group
    # 生成随机的points group 每组3个 因为3点确定一个平面
    # 抽sample_time组，每组抽3个 
    selected = np.random.choice(np.arange(noise_points.shape[0]), size=(sample_time,3), replace=False) #(sample_time,3)
    selected_points = noise_points[selected] #(sample_time,3,3)
    
    # estimate the plane with sampled points group  
    # 用选择的点集来生成平面
    planes_parameter = get_plane(selected_points) #（sample_time，4） 每组的4个ABCD参数 一共sample_time组
    cnt = np.zeros(sample_time) #每组有多少个内点

    #evaluate inliers (with point-to-plance distance < distance_threshold)
    #计算生成的平面的内点数量
    #获得对每组来说 130个点是否是内点 是为1 不是为0
    result = np.apply_along_axis(is_inliers, 1, noise_points, planes_parameter, distance_threshold) #(130,st）
    cnt = np.sum(result,axis = 0) #(st,)
        
    # minimize the sum of squared perpendicular distances of all inliers with least-squared method 
    # 用内点最多的一组来作为参数 依据该组的局内点用最小二乘法拟合平面 
    max_idx = np.argmax(cnt)
    #最好的一组的内点
    optimal_points_idx = result[:,max_idx] #(130,) 0 or 1 代表是否是内点
    optimal_points = noise_points[optimal_points_idx==1] #(103,3)这样子

    x = optimal_points[:,0]
    y = optimal_points[:,1]
    z = optimal_points[:,2]
    #ax+by+d=z
    data = np.column_stack((x, y, np.ones_like(x)))
    result_para, _, _, _ = np.linalg.lstsq(data, z, rcond=None)
    optimal_A = result_para[0]
    optimal_B = result_para[1]
    optimal_C = -1
    optimal_D = result_para[2]
    pf = [optimal_A, optimal_B, optimal_C, optimal_D]
    # draw the estimated plane with points and save the results 
    # check the utils.py for more details
    # pf: [A,B,C,D] contains the parameters of palnace function  A*x+B*y+C*z+D=0  
    draw_save_plane_with_points(pf, noise_points,"result/HM1_RANSAC_fig.png") 
    np.savetxt("result/HM1_RANSAC_plane.txt", pf)

5.MLP的反向传播

这个任务让我们手写一个MLP的反向传播。

http://cs231n.stanford.edu/handouts/linear-backprop.pdf

 MLP（全连接神经网络）的反向传播 - 知乎

【官方双语】深度学习之反向传播算法 上/下 Part 3 ver 0.9 beta_哔哩哔哩_bilibili

理解了之后代码就不难写

# Backward : compute the gradient of paratmerters of layer1 (grad_layer_1) and layer2 (grad_layer_2)

        
        delta_2 = pred_y - gt_y  # delta_2 = dL/dz2
        grad_layer_2 = output_layer_1_act.T.dot(delta_2) # grad_layer_2 = dL/dw2

        delta_1 = delta_2.dot(MLP_layer_2.T) * output_layer_1_act * (1 - output_layer_1_act) # delta_1 = dL/dz1
        grad_layer_1 = input_vector.T.dot(delta_1) # grad_layer_1 = dL/dw1

        MLP_layer_1 -= lr * grad_layer_1 #需要优化的参数 两层的W
        MLP_layer_2 -= lr * grad_layer_2

最终结果如下：