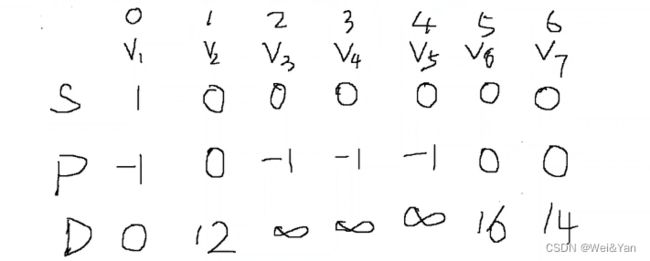数据结构 -最短路径dijkstra（迪杰斯特拉）算法讲解及代码实现

        迪杰斯特拉算法是一种广义的贪心算法，求出局部最优解，再去求全局最优解

图文讲解：

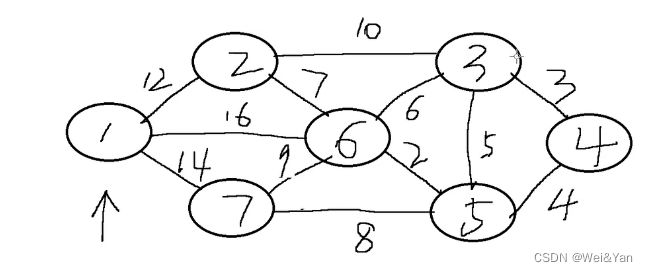
举例图：（起始点为1）

辅助数组：

s：记录了目标顶点到其他顶点的最短路径是否求得（求得为1，否则为0）

p：目标顶点到其他顶点的最短路径的前驱节点

（如，求得1->7->5的最短路径，那么5的前驱节点为7）

d：记录目标顶点到其他顶点最短距路径的长度 

首先利用二维数组构建图中各个顶点的辅助数组的初始化关系：

初始化的解析：初始化只知道目标顶点：顶点1到自己的最短路径也就是0，所以s1为1其余没有求得标记为0，p中目标顶点v1到1 3 4 5顶点都没有弧也就是没有目标顶点到此节点的前驱节点设为-1，

d为目标顶点v1到与他有弧的节点的弧长度（权重），没有弧的则设置为无穷（32767） 

 步骤：（x集合为记录已经找到最短路径的节点，最初x：v1（目标节点））

1.每次从d中找到最小的数，并找到其节点下标，将此节点的s标记为1意味已找到目标节点到此节点的最短路径，再把此节点加入到我们的x集合当中。

2.把已经找到的最小路径的节点当作中专点，判断目标顶点到当前节点的路径+当前节点到其他节点的路径是都小于目标节点到其他节点的路径长度，如过小于则更新目标节点的长度。

（如v1-v3为无穷，v1-v2-v3为22，小于无穷所以把v1-v3的路径改为22：d2为22）

3.重复1，2的操作直到x集合标记完所有节点（s数组元素全部为1）。

代码实现：

#include 
#include 
#define MAX 32767
typedef struct Graph
{
	char* vexs;//顶点
	int** arcs;//边（用二级指针存放存放边的一级指针，一级指针存放边）
	int vexsNum;//顶点的个数
	int arcsNum;//边的个数
}Graph;

Graph* initGraph(int vexNum)
{
	Graph* G = (Graph*)malloc(sizeof(Graph));
	G->vexs = (char*)malloc(sizeof(char)*vexNum);
	G->arcs = (int**)malloc(sizeof(int*)*vexNum);
	for (int i = 0; i < vexNum; i++)
	{
		G->arcs[i] = (int*)malloc(sizeof(int) * vexNum);
	}
	G->vexsNum = vexNum;
	G->arcsNum = 0;
	return G;
}

void crativeGraph(Graph* G, char* vexs, int* arcs)
{
	for (int i = 0; i vexsNum; i++)
	{
		G->vexs[i] = vexs[i];//（Graph中的顶点数组存放顶点的“名字”）
	for (int j = 0; j < G->vexsNum; j++)
		{
			G->arcs[i][j] = *(arcs + i * G->vexsNum + j);//二维数组加一个数表示第i+1个元素（相当于把二维数组全排成一行）                                                            
			if (G->arcs[i][j] > 0 && G->arcs[i][j] != MAX)
				G->arcsNum++;//统计边的个数（二维数组中有边则元素为1） //这里的图为带权重的图所以再统计边的时候二维数组元素既要大于0也要不为无穷                                                                  
		}
	}
	G->arcsNum /= 2;//（二维数组计算了两次边的次数）
}
//DFS深度优先遍历的访问
void DFS(Graph* G, int* visited, int index)
{
	if (index==4)
	{
		printf("%c ", G->vexs[index]);
		visited[index] = 1;
	}
	else
	{
		printf("%c->", G->vexs[index]);//先打印出顶点
		visited[index] = 1;//再把访问过的顶点做标记
	}
	for (int i = 0; i < G->vexsNum; i++)
	{
		if (G->arcs[index][i] > 0 && G->arcs[index][i] != MAX && !visited[i])//因为为带权重的图所以dfs访问的时候边的条件也是要满足>0且!=无穷两节点才有边
		{
			DFS(G, visited, i);
		}
	}
}
void dijkstra(Graph* G,int index)
{//准备辅助数组
	int* s = (int*)malloc(sizeof(int) * G->vexsNum);//记录最短路径是否求得（1是，0否）
	int* p = (int*)malloc(sizeof(int) * G->vexsNum);//记录目标顶点到其他顶点的最短路径的前驱节点
	int* d = (int*)malloc(sizeof(int) * G->vexsNum);//记录了目标顶点到其他顶点的最短路径长度
	//初始化辅助数组
	for (int i = 0; i < G->vexsNum; i++)
	{//最初我们只知道目标顶点到自己的最短路径
		if (i == index)
			s[i] = 1;
		else
			s[i] = 0;
	}
	for (int i = 0; i < G->vexsNum; i++)
	{
		if (G->arcs[index][i] > 0 && G->arcs[index][i] != MAX)
			p[i] = index;//如果节点与目标节点有弧则将此节点的前驱节点设为目标节点

		else
			p[i] = -1;
	}
	for (int i = 0; i < G->vexsNum; i++)
	{
		if (G->arcs[index][i] > 0 && G->arcs[index][i] != MAX)
			d[i] = G->arcs[index][i];
		else
			d[i] = MAX;
		if (i == index)
			d[i] = 0;
	}
	printf("最初图 的辅助数组\n");
	for (int i = 0; i < G->vexsNum; i++)
	{
		printf("%d %d %d\n", s[i],p[i],d[i]);//三个数组是竖着输出的
	}
	
	for (int i = 0; i < G->vexsNum - 1; i++)
	{
		int index = getMin(d,s,G);
		s[index] = 1;//将s数组数组元素改为1意味着：已经找到起始节点到此节点的最短路径
		for (int j = 0; j < G->vexsNum; j++)
		{//将返回的节点作为中转点
			if (!s[j] && d[index] + G->arcs[index][j] < d[j])//判断v1到中专点的距离+到其他节点的距离和是否小于v1到其他节点的距离
			{
				d[j] = d[index] + G->arcs[index][j];//如果小于则更新v1-此节点的最短路径
				p[j] = index;//并且将此节点的前驱节点改为中转点
			}
		}
	}
	printf("最短路径的图的辅助数组\n");
	for (int i = 0; i < G->vexsNum; i++)
	{
		printf("%d %d %d\n", s[i], p[i], d[i]);
	}
}
int getMin(int* d, int* s, Graph* G)
{
	int min = MAX;
	int index = 0;
	//找与起始节点有弧的且弧长度最小（权重最短）的节点，并且返回此节点的下标
	for (int i = 0; i < G->vexsNum; i++)
	{
		if (!s[i] && d[i] < min)
		{
			min = d[i];
			index = i;
		}
	}
	return index;
}
int main()
{
	Graph* G = initGraph(7);
	//创建深度优先遍历的时候判断该顶点是否被访问的数组
	int* visited = (int*)malloc(sizeof(int) * G->vexsNum);
	for (int i = 0; i < G->vexsNum; i++)
	{
		visited[i] = 0;//先把每个元素都设为0，当被访问过的时候就改变元素的值
	}
	//提前根据图的数创建出符合其边的关系的二位数组
	int arcs[7][7] =
	{
		0,12,MAX,MAX,MAX,16,14,
		12,0,10,MAX,MAX,7,MAX,
		MAX,10,0,3,5,6,MAX,
		MAX,MAX,3,0,4,MAX,MAX,
		MAX,MAX,5,4,0,2,8,
		16,7,6,MAX,2,0,9,
		14,MAX,MAX,MAX,8,9,0
	};
	crativeGraph(G, "1234567", (int*)arcs);//节点的“名字”
	DFS(G, visited, 0);//这里我们把目标节点定位v1所以index传0
	dijkstra(G, 0);
	printf("\n");
	return 0;
}

“不看广告看疗效”

（辅助数组我们都是竖着输出的）

最后我们可以通过辅助数组找到目标节点到任何节点的最短路径

eg：目标节点-v5

1.先找v5的前驱节点v6，路径为18

2.找v6的前驱节点为v1，路径为16

所以v1-v5的路径为v1-v6-v5，最短路径为18+16=34.