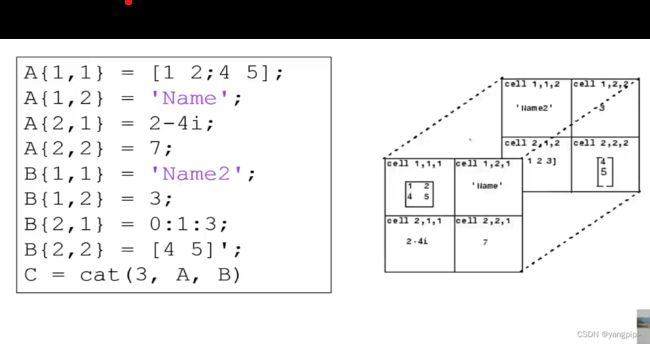
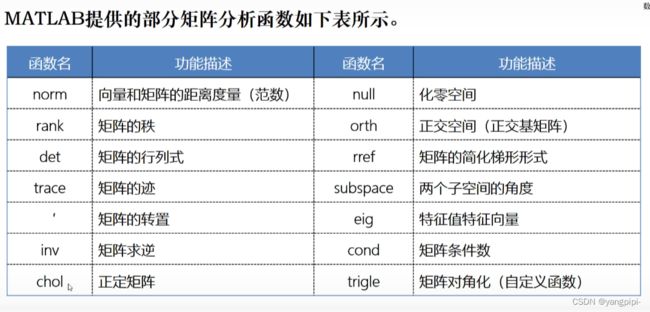
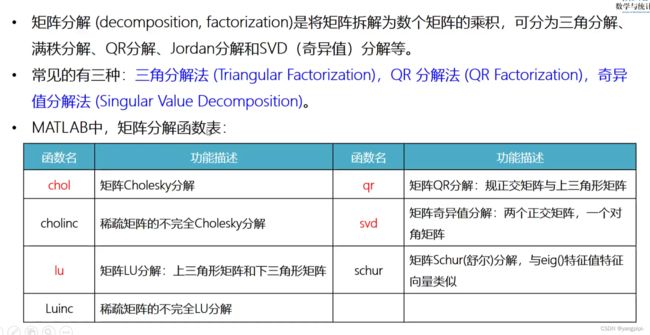
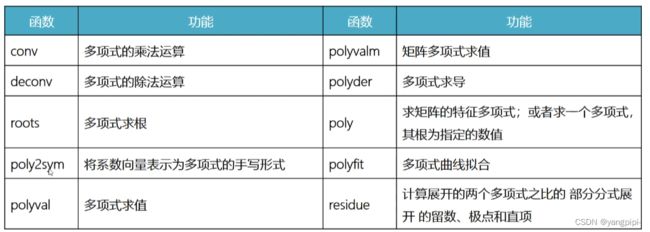
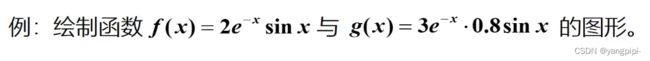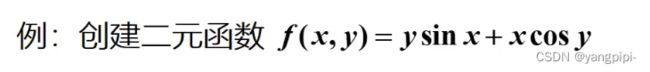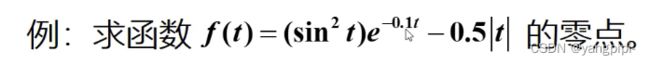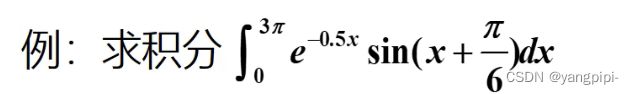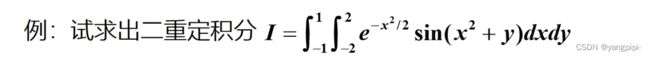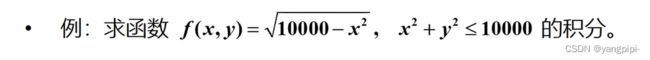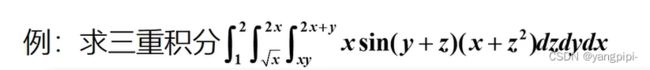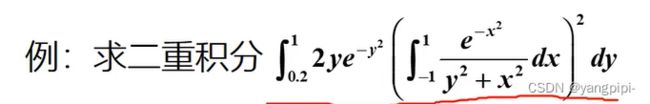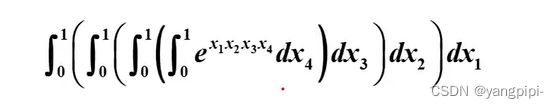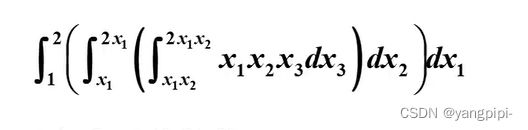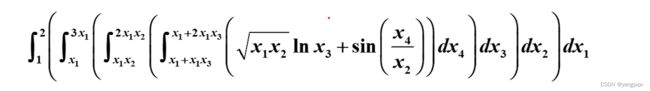Matlab
编程基础
-
%表示注释,%%可以分块(在分块中点击Ctrl+回车就会只运行所在的分块里面的内容).
-
数据leix:
-
class(变量):可以查看变量的类型
-
help 脚本名字:会输出开头的注释 -
注释:
%{ 计算圆的周长计算圆的周长%} -
输入一个数字,会自动存到ans中,当以;结尾时,内容就不会显示,但是命令执行了
-
...表示续行符 -
设置断点时发现断点是黑色:
表示脚本未保存 -
clc清空命令行中的内容,clear清除工作区中的内容(显示变量的地方) -
上下键可以调出以前的命令
-
可以通过建立脚本然后运行的方式,运行命令
-
也可以通过选中脚本中的内容然后运行.
-
who/whos可以显示所有变量的名字 -
format compact容纳更多的结果 去掉显示的多余空行
-
可以在命令行中输入脚本文件的名字(后面不要添加后缀.m)脚本就会被执行
-
输入
1.111111111111发现并没有显示完全,只是显示了其中的一些,可以通过工作区点击变量就可以看到完整的变量
可以通过格式命令可以显示
format long e （15）
format short e （4）--默认
- 当在命令行中输入变量名后就会显示变量的值
- 当在循环中了i之后，i作为虚数单位的作用会消失，这是应该这样写
2+2*1i app_string = "" app_char = ''字符变量tr = truelogical类型- 指数形式:
2e10===2d10 - 不等于:
3~=2相当于编程语言中的1!=2 - 异或表达式:
xor(1>2,2<2)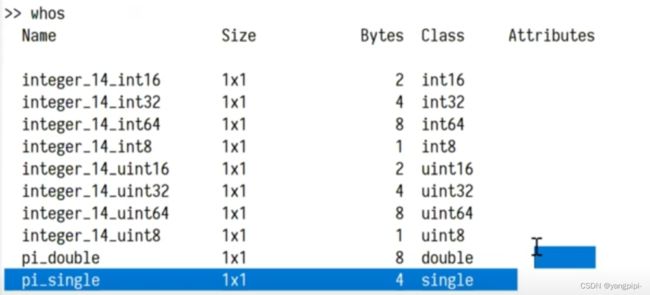 
10.x=1:5 === x:1:5 === x=linspace(1,5,1)
25. 当使用length去求一个矩阵的值时,求的是行和列中最大的一个值.
26. matlab数组的下标值从1开始
行元素:
a = [1,2,3] 等于 a=[1 2 3]
列元素
a=[1;2;3]等于
a=[
1
2
3]
冒号自动生成方式：
X=1：5；x=a:h:b；从起始值a开始，以增量h为步长，到终止值b结束的行向量。
x=linspace（a，b,n）：创建从a开始，到终止值为b结束，有n个元素的行向量。
一维数组的访问：
访问一个元素：x（i）表示访问x的第个元素访问一块元素：x（i:j:k）表示访问数组x，从i个元素开始，以步长j到第k个元素，j可以为负数，j缺省时默认为1访问指定元素：x（[i，j，k]）访问数组x中第i、j、k个元素，访问结果构成一个新数组[x（i），x（j），x（k）]
[1 2 3
4 5 6
7 8 9 ]
c[2]----是4
c[2:1]---是4
c[2,:]--是第二行所有元素
清楚一个元素或者一行使用:`[]`
- 如果想让两个2*3的两个矩阵对应元素两两相乘
c.*a除的话[c./b] 每个元素平方a.*2
%文件名:bengji.m
%% 1.求解微分方程的通解
syms m cd g v(t);
eq = diff(v,t) == g - cd/m*v^2;
sol = dsolve(eq);
cond = v(0) == 0;
sol = dsolve(eq,cond);
%% 2.符号表达式求值
vt = subs(subs(subs(sol, 'm',68.1), 'g',9.81), 'cd',0.25);
i = 1;
%% 3.循环求解在时间区间[0.20]内,自由落地的速度值
for ti = 0:20
vval(i) = double(subs(vt,'t',ti));
i = i+1;
end
%% 4.对时间0-20s内的速度进行可视化绘图
tf = 0:20
%% 5.绘图函数plot
plot(tf,vval,'-','LineWidth',2)
title("自由落地速度随时间变化曲线")
xlabel("时间t(s)")
ylabel("速度(m/s)");
grid on
hold on
plot(12,vval(13),'r.','MarkerSize',15,'MarkerFaceColor','red') %vval(13)表示第13个值,标记其中的某个点
%text(12,vval(13),num2str(vval(13)))%原始的这个,但是会盖住头像.
text(12,vval(13)+3,num2str(vval(13)),'HorizontalAlignment','center') %数值转换成字符串的函数:num2str()
%% 5.蹦极运动员的极限速度
limS =double(limit(vt,'t',inf))
- hold on：保持原图并接受此后绘制的新的曲线，叠加绘图
hold off：重新刷新图形窗口，绘制新的曲线 - legend(“近似解”,‘解析解’); ----添加图例
%文件名:bungeeS
% 函数文件：输入参数 输出参数
function vt = bungeeS(m,cd,th,tend)
%% m表示蹦极运动员的质量,cd表示集总阻力系数,th表示时间步长,tends表示时间tend秒之前
g = 9.81; %重力加速度
vbefore = 0; %相当于迭代公式的v(ti)
vnext = 0; %相当于迭代公式的v(t(i+1))
i = 1;
for ti = 0:th:tend
vnext = vbefore + (g - cd/m*vbefore^2)*th; %迭代公式
vt(i,1) = ti; %第一列存储时间
vt(i,2) = vbefore; %第二列存储每时刻的速度值.
i = i + 1;
vbefore = vnext; %速度值的迭代
end
%% 图话上述脚步产生的数据
plot(vt(:,1),vt(:,2),'b-','LineWidth',1)%所有行的第一列作为横坐标,采用红线进行绘制
title("自由落地速度随时间变化曲线-采用数值解")
xlabel("时间t(s)")
ylabel("速度(m/s)")
grid on
hold on
bengji
legend("近似解",'解析解','Location','best')
str = strcat("数值是: ",num2str(22));
disp(str);
- save(“data.mat”);---------load(“data.mat”);
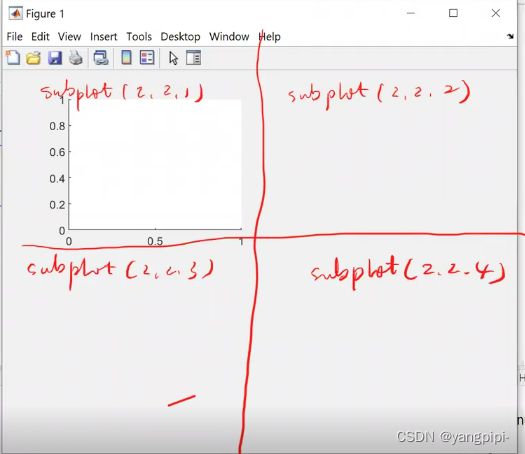
- 一张纸画多个图,subplot
x = 0:0.01:2*pi;
y = x + i*x.*sin(x);
plot(y);
subplot(2,1,1)
title("第一张图");
plot(y);
x2=0:1:100
y2 = 2*x2·
subplot(2,1,2);
title("第二张图");
plot(x2,y2)
- 里面的角度只能是弧度，所以必须进行转化:
pi/180*60‘’
系统内置函数
其他函数
- IO函数
x = 0:pi/10:pi;
y = sin(x);
fid = fopen('sin.txt','w');
for i = 1:11
fprintf((fid),'%5.3f %8.4f',x(i),y(i));
end
fclose(fid);
- 输入函数: rad = input("请输入内容: ")
用法一：
>> letter = input("请输入一个数字: ")
请输入一个数字: 12
letter =
12
> whos
Name Size Bytes Class Attributes
letter 1x1 8 double
用法二：
>> letter = input("请输入一个字符: ",'s')
请输入一个字符: 12
letter =
'12'
>> whos
Name Size Bytes Class Attributes
letter 1x2 4 char
用法三：
>> R = 122
R =
122
>> letter = input("请输入一个字符: ")
请输入一个字符: R
letter =
122
用法四：
>> letter = input("请输入一个字符: ")
请输入一个字符: R
letter =
122
>> letter = input("请输入一个字符: ")
请输入一个字符: 'letter'
letter =
'letter'
>> letter = input("请输入一个字符: ",'s')
请输入一个字符: 'letter'
letter =
''letter''
用法五:
>> vec = input("请输入一个数组： ")
请输入一个数组： [1 2 3 4]
vec =
1 2 3 4
用法六:%s和%c的区别:
>> fprintf("%c\n",[97 97]);
a
a
>> fprintf("%s\n",[97 98]);
ab
>> fprintf("%c\n",[97 98]);
a
b
- 写文件操作:
>> mybat = rand(2,3)
mybat =
0.756669787984348 0.293555594417440 0.375091630987986
0.796106235942840 0.115206746018031 0.82889374505677
save testfile.dat mybat -ascii
type testfile.dat % 显示文件内容
- type testfile.dat %··
- save testfile.dat mybat -ascii -append
以追加的形式写入文件
练习1:
col = input("请输入行数: ");
row = input("请输入列数: ");
mybat = randi([1,100],[col,row]);
save mybat.dat mybat -ascii
- 读取文件内容:load testfile.dat 会生成一个testfile变量的矩阵
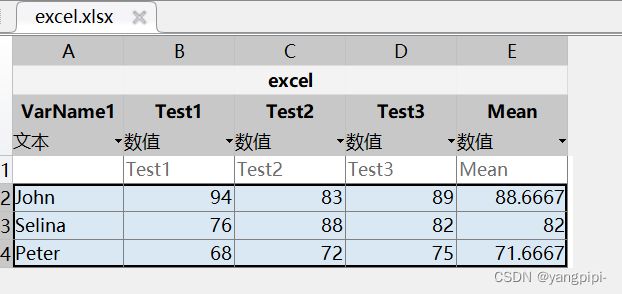
- 从excel中读取数据
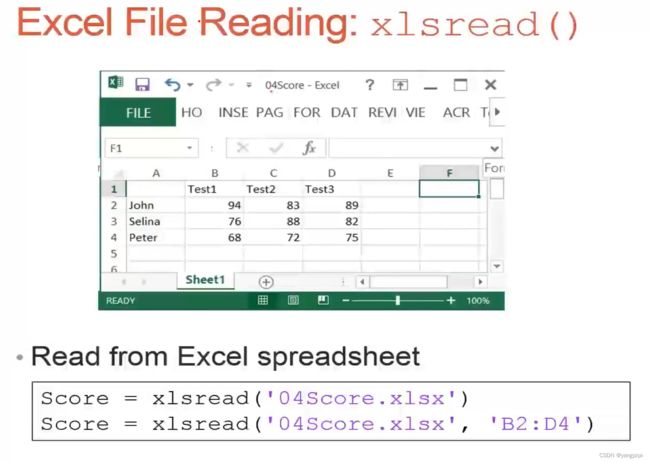
其实上面的两种读取方法是一样的,都只会读取数据，上面的B2:D4是excel中的表格各个行的表示
练习1:
读取excel表格数据
>> Score = xlsread('excel.xlsx')
Score =
94 83 89
76 88 82
68 72 75
>> Score = xlsread('excel.xlsx','B2:D4')
Score =
94 83 89
76 88 82
68 72 75
计算平均值，并将平均值存入excel中
>> M = mean(Score')'
M =
88.6667
82.0000
71.6667
>> xlswrite('excel.xlsx',M,1,'E2:E4')
>> xlswrite('excel.xlsx',{'Mean'},1,'E1')
计算标准差并写入到excel表格中
E = [];
sum = 0;
for i = 1:3
sum = 0;
for j = 1:3
sum = sum + (Score(i,j)-M(i)) ^ 2;
end
E = [E,sqrt(sum)/3];
end
xlswrite('excel.xlsx','standDeviation'},1,'F1')
xlswrite('excel.xlsx',E',1,'F2:F4')
读取excel表格中的各行和各列表示
>> [Sco Header] = xlsread("excel.xlsx")
Sco =
94.0000 83.0000 89.0000 89.0000 2.5963
76.0000 88.0000 82.0000 82.0000 2.8284
68.0000 72.0000 75.0000 71.6667 1.6555
Header =
4×6 cell 数组
{0×0 char} {'Test1' } {'Test2' } {'Test3' } {'Mean' } {'standDeviation'}
{'John' } {0×0 char} {0×0 char} {0×0 char} {0×0 char} {0×0 char }
{'Selina'} {0×0 char} {0×0 char} {0×0 char} {0×0 char} {0×0 char }
{'Peter' } {0×0 char} {0×0 char} {0×0 char} {0×0 char} {0×0 char }
- strcat(“str1”,“str2”);strcmp(s1,s2);strncmp(s1,s2,3);
- 不在乎是否大小写:strcmpi(s1,s2) == strcmp(upper(s1),upper(s2))
- str = sprintf(“%d\n”,12); 格式化输出
- erase(string,要去掉的字符串)
- 小写:lower() 大写:upper()
- strjoin() ; 可以将容器中的数据连接为一个字符串
随机函数
1、rand（）
功能：生成0-1之间的伪随机数
e.g. rand(3) 生成一个3*3的0-1之间的伪随机数矩阵
rand(a,b)生成a行b列的矩阵
2、randn（）
功能：生成标准 正态分布的伪随机数(均值为0，方差为1)
2、randn功能：生成标准正态分布的伪随机数(均值为0，方差为1)
rand（）是产生随机数的，每一次产生的都不一样，这样才叫做随机数。但是，有些情况，如果我需要随机数是一样的，我需要跟踪一下，那怎么办？
3、用rng函数控制随机数。
4. randi([a,b])生成(a,b)之间的整数随机数
randi([a,b],3,4)生成3x4的矩阵;从(a,b)之间取
数学中的简单函数
- fix()取整–直接去掉小数 向零取整 fix(-3.2) == -3
- floor() 地板 向无穷取整 floor(-3.2) == -4
- ceil() 天花板
- round() 四舍五入 round(x,2)取2位小数
- mod/rem函数都是取余函数
- sign()符号函数 为正数返回1，符号为-1,0为0，NaN为NaN
- deg2red() 角度转化为弧度(radian)
- log()这个是以e为底,log2()以2为底,log10()以10为底
- exp()以e为底，自然常数e是
exp(1) - isletter()
>> isletter('a')
ans =
logical
1
>> isletter('abc')
ans =
1×3 logical 数组
1 1 1
>> isletter('___1')
ans =
1×4 logical 数组
0 0 0 0
>> isletter('___1a')
ans =
1×5 logical 数组
0 0 0 0 1
- isempty()
- isa() 判断变量的类型
>> isa(a,'double')
ans =
logical
1
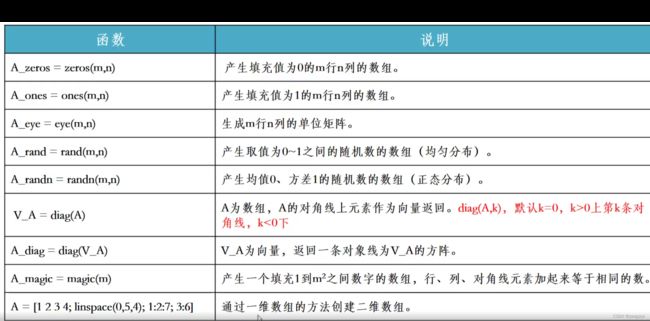
矩阵
-
产生数组:
- [1 2 3 4 4] ;
- [1:2:10]:从1开始10结束,每次+2 ;
- [10:1:0]从10开始0结束，每次-1；
- linspace(1,10,7)从从1到10之间取10个数
- logspace(1,10,7)从10到 10^10之间的7个数
- [1;2;3]产生一个列向量或者
[1,2,3]'注意如果是复数使用'转置会产生共轭转置[1+1i;2+2i]'==[1-1i;2-2i]如果想取消共轭转置的设置:[1+1i;2+2i].' - rand(2,3)
-
List item
- randi([1,10],3,4)
- ones(3)
- zeros(3)
- eye(3)生成3维单位矩阵
- a=[1 2 3 4] diag(a)生成对角线上元素为a的矩阵
- diag(A)：取出A矩阵中的对角线上的元素
- 将次对角线上的元素进行设置; diag(1:1:10,-1) 对角线(diagonal)
- matlab 中矩阵和数组
一维数组相当于向量，二维数组相当于矩阵。所以矩阵是数组的子集
数组Q运算是指数组对应元素之间的运算，也称点运算.矩阵的乘法、乘方和除法有特殊的数学含义，并不是数组对应元素的运算，所以数
组乘法、乘方和除法的运算符前特别加了一个点。
矩阵Q是一个二维数组，所以矩阵的加、减、数乘等运算与数组运算是一致的。但有两点要注意：
（1）对于乘法、乘方和除法等三种运算，矩阵运算与数组运算的运算符Q及含义都不同：矩阵运算按线性变换定义，使用通常符号；数组
运算按对应元素运算定义，使用点运算符；
（2）数与矩阵加减、矩阵除法在数学是没有意义的，在MATLABQ中为简便起见，定义了这两类运算
引用自](https://blog.csdn.net/nanhuaibeian/article/details/96437934)
15. 生成一个三维数组:
T(:,:,1) = randi([1,9],[3,4])
T(:,:,2) = randi([1,9],[3,4])
T(:,:,3) = randi([1,9],[3,4])
>> T
T(:,:,1) =
9 8 7 6
6 9 7 2
1 7 4 7
T(:,:,2) =
5 6 3 9
9 3 5 9
4 7 7 5
T(:,:,3) =
2 8 3 2
2 3 9 3
3 8 4 6
>> whos
Name Size Bytes Class Attributes
T 3x4x3 288 double
- 特殊矩阵
1. E = []
作用:可以用来在循环中存储数据
>> E = [E,randi([1,6])]
E =
3
>> E = [E,randi([1,6])]
E =
3 5
>> E = [E,randi([1,6])]
E =
3 5 1
>> E = [E,randi([1,6])]
E =
3 5 1 3
>> E = [E,randi([1,6])]
E =
3 5 1 3 6
>> E = [E,randi([1,6])]
E =
3 5 1 3 6 5
注意:不要使用[nan(1,4),E]进行合并
-
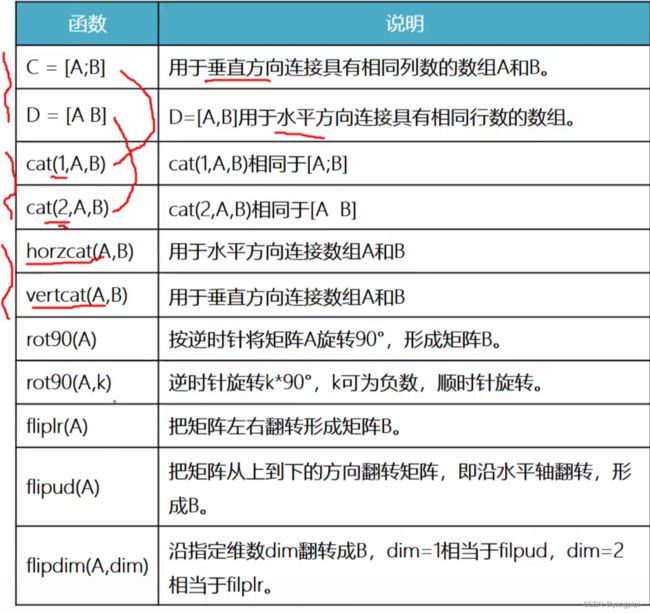
合成向量 [A B] VS [A;B]
-
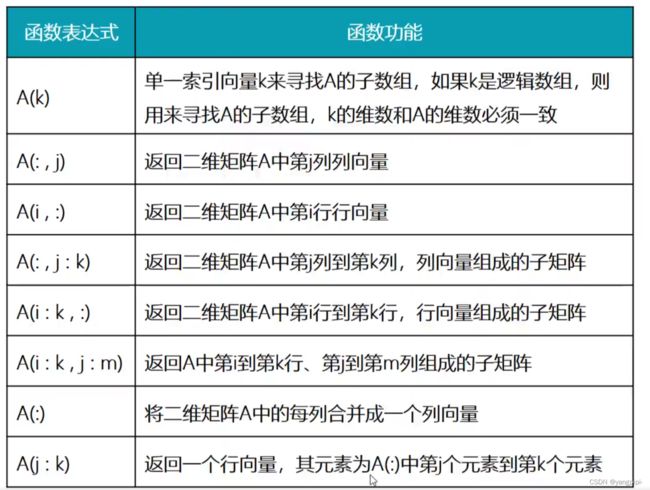
访问向量的元素
- A(1) 从0开始
- A([2 1 3])访问2 1 3 位置的元素
- A(end)访问最后一个元素
- A(100) = 12 注意当没有100个数据时，此操作会造成会将有元素的位置到100之间的位置填充0
- 注意对于列向量和行向量访问元素时返回的类型根据要访问的元素的类型确定,是行向量则返回行向量,是列向量则返回列向量
-
矩阵的访问
1. A(1,2) 2. A(2)是A(2,2) 3. 访问第一行:`A(1,:）` 4. 可以集体复制,只要等号最有两边维数相同即可 1. 特例:给一行赋值:`A[1,:]=9`这个是可以的 2. A(1:2,1:2) = 2这个也是可以的- M */-+ 3 都是3与每一个元素进行操作
>> A = [1 21 6;5 17 9;31 2 7]
A =
1 21 6
5 17 9
31 2 7
>> A([1 3;1 3])
ans =
1 31
1 31
A([1 3;1 3]) 就是 将A[1 3]得到的元素和A[1 3]得到的元素合成为一个矩阵
--------------------------------------------------------------------------------
>> A([1 3],[1 3]) 就是分别取出A(1,1),A(1,3),A(3,1),A(3,3)
ans =
1 6
31 7
- 访问矩阵内部的子式
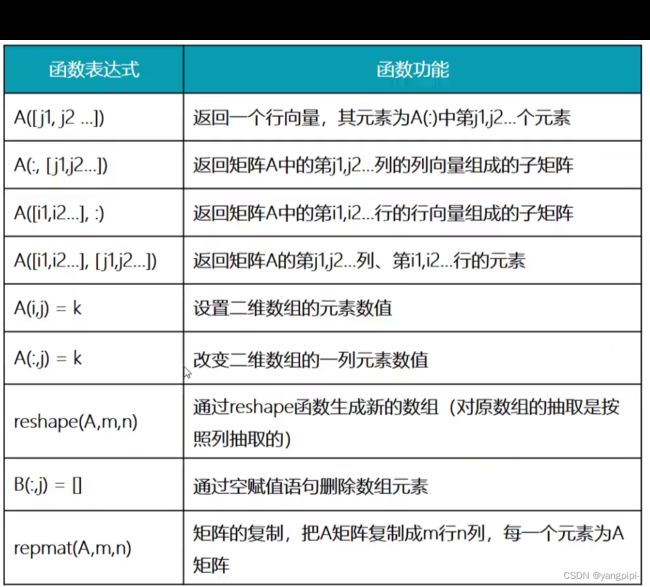
练习1:
去掉矩阵中的第三行元素:
>> A = A([1,2],:)
>> A(3,:) = []
- 操作矩阵的函数
-
总的规律:当函数操作于行数为1的矩阵时，函数时对于所有的数进行操作并且返回一个结果。但是当函数操作于矩阵大于1的矩阵时是分别操作于每一列的元素并且返回列数个结果
-
-
length()返回矩阵列数与行数中的最大值
-
size() 返回：行数x列数
- 用法一: arr = size(A) arr是一个行向量
- 用法二:[a1,a2] = size(A),a1变量存储行数。。。。
-
reshape(M,2,6)改变矩阵
-
flipud(M):上下翻转
-
fliplr(M):左右翻转
-
flip()
-
rot90()逆时针翻转90
-
将线性坐标转化为二维坐标:ind2sub()
-
>> V1 = randi([1 9],[3 3])
V1 =
7 9 2
5 9 6
4 6 4
>> find(V1==9)
ans =
4
5
>> [i,j]= ind2sub(size(V1),find(V1==9))
i =
1
2
j =
2
2
11.
12. rempat()：已矩阵为单位进行扩充
>> A = [1,2;3,4]
A =
1 2
3 4
>> B = [A,A,A;A,A,A]
B =
1 2 1 2 1 2
3 4 3 4 3 4
1 2 1 2 1 2
3 4 3 4 3 4
>> repmat(A,2,3)
ans =
1 2 1 2 1 2
3 4 3 4 3 4
1 2 1 2 1 2
3 4 3 4 3 4
9. repelem
>> A
A =
1 2
3 4
>> repelem(A,2,3)：以矩阵中的每一个元素为单位进行扩充
ans =
1 1 1 2 2 2
1 1 1 2 2 2
3 3 3 4 4 4
3 3 3 4 4 4
10. nan：
X = NaN 返回非数字的标量表示。之所以出现 NaN，是因为运算返回了未定义的数值输出，如 0/0 或 0*Inf。
X = NaN(n) 返回 NaN 值的 n×n 矩阵。
11. diff(M)：数组中的元素,后一项减去前一项,那么:输出后的结果维数都会少一: 1x4输出1x3,2x2输出1x2
12. -----下面的函数操作与以为数组，是对所有元素进行操作，但是对于超过一维的矩阵则是分别对每列进行操作
13. sum()
14. max()
max函数的使用
>> A
A =
1 21 6
5 17 9
31 2 7
>> max(A)
ans =
31 21 9
>> max(max(A))
ans =
31
15. prod()：矩阵所有元素的相乘之后的结果
16. sort()
sort(A)将每一列上的元素进行排列
sortrows(A)将每一行上的元素进行排列
17. cumsum()：
>> a = [1:10]
a =
1 2 3 4 5 6 7 8 9 10
>> cumsum(a)
ans =
1 3 6 10 15 21 28 36 45 55
16. cumprod()同上
17. cummin()同上
18. cummax()同上
- 矩阵与矩阵
- A +/-B一一对应
- A
.*B一一对应相乘 - A
./B一一对应相除 - A.^B 一一对应幂运算
5.q
1、&&针对标量运算，&可以用于向量或数组。
A = [0,0,1,1];
B = [0,1,01,];
C = A && B ;%错误使用 &&的操作数必须为标量值
C = A & B ; C=[0,0,0,1]
C = A>1& B<2正确
C = A(1)>1 && A(2)<2正确
2，&&运算具有短路功能，即 A && B , 如果A为0, 则不计算B，直接返回0。&运算没有短路功能，会计算全部的A、B值后求逻辑与。
3，&适用于符号运算，&&不适用。
原文链接：https://blog.csdn.net/naturly/article/details/106966412
6. 矩阵的逻辑操作
res = M>5
M(res);返回为真的元素
手动造一个逻辑数组:
v = [1 0 1 0] %这个是不起作用的
v = logical([1 0 1 0])
6. 逻辑操作函数---`all() any()`
>> any([1 0])
ans =
logical
1
>> any([0 0])
ans =
logical
0
>> all([1 1 2])
ans =
logical
1
>> all([1 1 0])
ans =
logical
0
数组R中的所有数是否都大于0.1
all(R>0.1)
列 1 至 44
1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
两个矩阵是否相同:
>> v1=[1:5]
v1 =
1 2 3 4 5
>> v2=[1:5]
v2 =
1 2 3 4 5
>> all(v1==v2) 但是只能比较维数相同的不同会返回erro
ans =
logical
1
>> isequal(v1,v2) 两个矩阵是否相同使用isequle()
ans =
logical
0
7.find() 根据逻辑值找出为1的元素的位置
>> R = [1 2 3 4 5]
R =
1 2 3 4 5
>> R_big_1 = R>3
R_big_1 =
1×5 logical 数组
0 0 0 1 1
>> find(R_big_1)
ans =
4 5
find(R_big_1,3,'first')：找到R_big_a中前三个逻辑为真的部分
练习1:找出vec数组中大于0的数并且输出
>> vec
vec =
11 -5 33 2 8 -4 25
>> way1_positive = vec(vec>0) 方法1
way1_positive =
11 33 2 8 25
>> way2_positive = vec(find(vec>0))方法2
way2_positive =
11 33 2 8 25
上面神奇的逻辑数组:
vec>1输出；逻辑值(0/1)
但是vec(vec>1)输出大于1的真是值
练习2:已知数组:V = randi([0 1],[1,1000])：1000个0或者1组成的数组，找出1与0变化的位置，并且算出有几个?
V = randi([1 0],[1,1000])
posi = find(diff(V)==1)
numel(posi)
sum(posi)
练习3:已知数组:V = randi([0 2],[1,1000])：1000个0或者1或者2组成的数组，找出1与0变化的位置，并且算出有几个?
方法一:将元素为1的0位置置为NaN，然后采用练习2的方法
V = randi([0 2],[1,1000])
V_tmp = V
V_tmp(V_tmp==0)=NaN
sum(diff(V_tmp))
方法二:
V1 = U(1:end-1);
>> V1 = U(2:end);
>> sum(V1==2&V2==1)
- 矩阵的乘法
1. V1 * V2
2. 矩阵的内积:
- 内积的概念: V1 = [a1,a2,a3] V2 = [b1,b2,b3] V1与V2的内积:a1b1+a2b2+a3*b3
- 方法一: sum(V1.V2)
- 方法2::V1V2'
3. C = cross(A,B) 返回 A 和 B 的叉积。
元胞数组（Cell）
- 可以存放不同的数据类型
>> [1 '1' "1"]
ans =
1×3 string 数组
"1" "1" "1"
>> {1 '1' "1"}
ans =
1×3 cell 数组
{[1]} {'1'} {["1"]}
- 访问:
{}()
cell =
1×3 cell 数组
{[111]} {["345"]} {'789'}
>> cell{1}
ans =
111
>> cell[1]
cell[1]
↑
错误: 表达式无效。调用函数或对变量进行索引时，请使用圆括号。否则，请检查不匹配的分隔符。
>> cell(1)
ans =
1×1 cell 数
{[111]}
- 删除元素: cell(2) = []
5.
cell_data = {[1 2 3;4 5 6],'Anne Smith',3+2i,-pi:pi:pi};
% 读取数据
>> cell_data(1,1)
ans =
1×1 cell 数组
{2×3 double}
% 读取cell里面中的矩阵中的某个元素
>> cell_data{1,1}
ans =
1 2 3
4 5 6
>> cell_data{1,1}(1,1)
ans=
1
struct
struct的建立
- student.name= 1;student.grade = 122
A = struct('data',[3 4 7;8 0 1],'next',struct('textnum','Test 1','xdata',[4 2 8],'ydata',[7 1 6]));
A(2).data = [9 3 2;7 6 5];
A(2).next.testnum = 'Test 2';
A(2).next.xdata = [3 4 2];
A(2).next.ydata = [5 0 9];
上面相当于创建了两个struct变量
A(1).data = [3 4 7;8 0 1]
A(1).next.textnum = 'Test 1'
.....
.....
A(2).data = [9 3 2;7 6 5];
A(2).next.testnum = 'Test 2';
A(2).next.xdata = [3 4 2];
A(2).next.ydata = [5 0 9];
add- struct内置函数
- 存图
练习1：
function practical(struct,field)
if isfield(struct,field)
disp(struct.(field)); % 注意这里
else
fprintf("Error %s is not a valid field",field)
end
end
当不知道元素的具体值时可以写空[]:tmp = struct('item_no',[],'cost',[],'price',[],'code',[])
复杂结构体
lineseg = struct('endpoint1',struct('x',2,'y',4),'endpoint2',struct('x',1,'y',6))
categorical数组
- 例子
1 表示小孩，2 表示青年 3表示老年
A = [...
3,2;...
3,3;...
3,2;...
2,1;...
3,2;...
];
Valueset = [1:3]
catnames = {'child','adult','senior'}
B = categorical(A,Valueset,catnames,'ordinal',true)% 后面的ordinary字段表示是否可以比较
B =
5×2 categorical 数组
senior adult
senior senior
senior adult
adult child
senior adult
>> B(4,1)
ans =
categorical
adult
>> B(1,1)
ans =
categorical
senior
>> B(4,2)<B(1,1)
ans
logical
1
Table
names = {'Harry','Sally','Jose'}
weights = [185;133;210]
heights= [74;65.4;72.2]
patients = table(weights,heights,'RowNames',names)
patients =
3×2 table
weights heights
_______ _______
Harry 185 74
Sally 133 65.4
Jose 210 72.2
>> patients(1:2,1)
ans =
2×1 table
weights
_______
Harry 185
Sally 133
>> patients("Harry",:)
ans =
1×2 table
weights heights
_______ _______
Harry 185 74
绘图
数学函数图像的绘制
fplot（二维函数图像绘制）
练习1：
>> gx = @(x)3*exp(-x);
>> gx = @(x)3*exp(-x).*sin(x);
>> fh = @(x)2*exp(-x).*sin(x);
>> gx = @(x)3*exp(-x).*sin(x);
>> xRange = [0,8];
>hold on
>grid on
>> fplot(gx,xRange,'b-o','LineWidth',1.5);
>> fplot(fh,xRange,'b-o','LineWidth',1.5);
% fplot(@填函数文件,xRange,'b-o','LineWidth',1.5);
fsurf(三维图像绘制)
练习1:
>> fh = @(x,y)y.*sin(x)+x.*cos(y);
>> fsurf(fh,[-10,10]);
fplot3（绘制三维参数方程曲线图）
练习1:
>> x=@(t)sin(t);
>> y=@(t)cos(t);
>> z=@(t)(t);
>> fplot3(x,y,z,[0,6*pi])
>> fplot3(x,y,z,'b-','LineWidth',15[0,6*pi])
简单的用法:
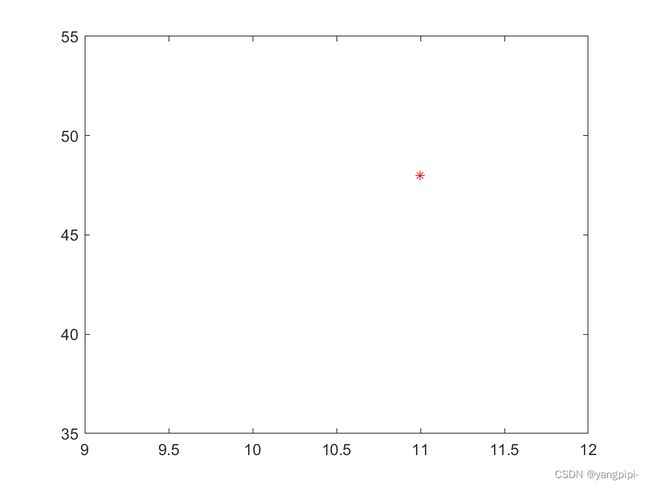
- 标注一个点为*:
%% 画图
x = 11;
y = 48;
plot(x,y,'*');
- 点标注为红色
%% 画图
x = 11;
y = 48;
plot(x,y,'*r');
- 设置坐标轴大小
%% 画图
x = 11;
y = 48;
plot(x,y,'*r');
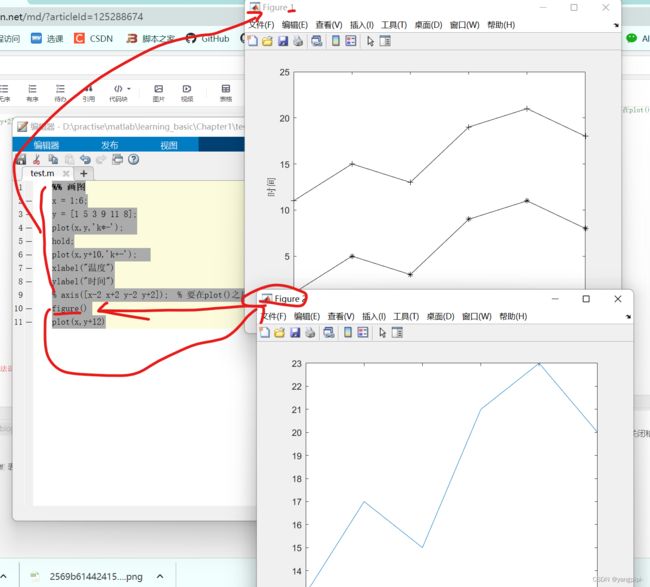
axis([9 12 35 55]); % 要在plot()之后axis(xmin xmax ymin ymax)
xlabel("时间")
ylabel(“温度”)
练习:
%% 画图
x = 11;
y = 48;
plot(x,y,'*r');
xlabel("温度")
ylabel("时间")
axis([x-2 x+2 y-2 y+2]); % 要在plot()之后axis(xmin xmax ymin ymax)
x = 1:6
y = [1 2 3 44 5 ]
% plot(x,y,'y') 等价于 plot(y,'y')设置颜色
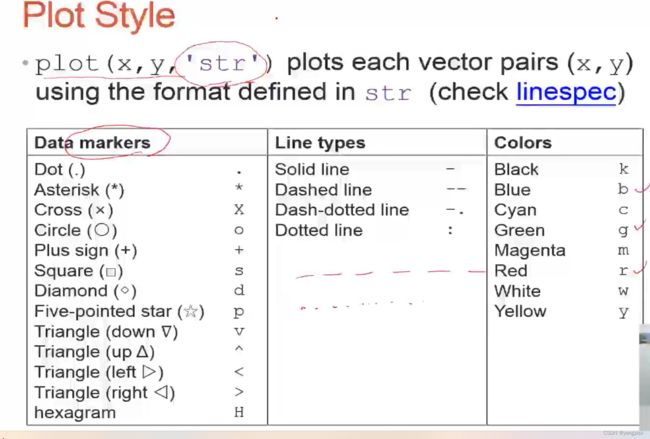
- 描点并且连线:
plot(x,y,'y*-')
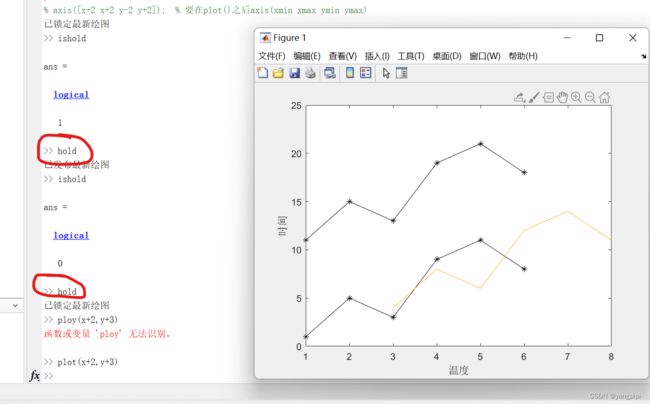
- 显示两个图
plot(x1,y1);
plot(x2,y2);
%只显示最后一个
plot(x1,y1);
hold;
plot(x2,y2);
- ishold()用于查看画布是擦画布的状态还是不擦画布的状态
- 也可以使用
hold on和hold off表示关闭和打开擦画布的状态 - figure()，重新打开一个窗口,编号默认为figure1，figur2…
figure(1)激活窗口1
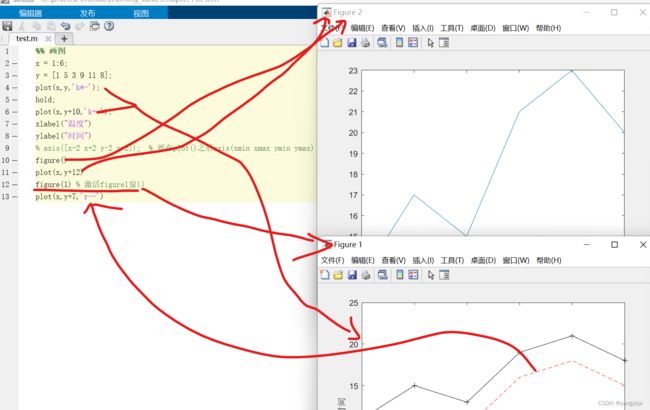
当在调试时，点击某个~~窗口~~画布就会激活这个窗口 画布 != 窗口
close all：表示关闭所有的窗口
close(1)清空figure1窗口
clf：表示清空当前激活的画布
一个figure窗口上可以有多个画布，每个画布都会有一个状态，所以不能说某个figure窗口的状态是激活还是非激活的
11. grid: 控制网格
figure;
plot(rand(3,1));
plot(rand(3,1),'x--');
hold on;
plot(rand(3,1),'o:')
plot(rand(3,1),'s-')
grid
grid：输出一次翻转一次
grid on
grid off
- 图例: legend(‘Line1’,‘Line2’,…)
- plot(1:0.1:10,sin(1:0.1:10),1:0.1:10,cos(1:0.1:10)) 同时画多个图
title(sprintf("Experiment Number %d",ExpNo));使用格式化输出标题- 修改图形
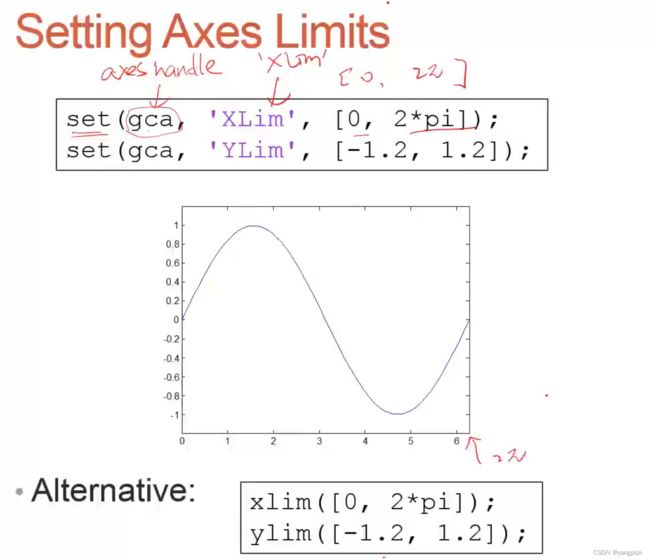
set(gca,'FontSize',25)
x=linspace(0,2.*pi,1000);
y=sin(x);
h = plot(x,y);
set(gca,'xlim',[0,2.*pi]);%设置x轴坐标范围
set(gca,'xtick',0:pi/2:2*pi);%设置x轴坐标间隔
set(gca,'XTickLabel',{'0','\pi/2','\pi','3\pi/2','2\pi'});%横轴上显示的是以π为单位
set(h,'LineStyle','-.','LineWidth',7.0,'color','g');
text()
- 在图形的指定位置显示指定的文字.
- 在图中标记某个点
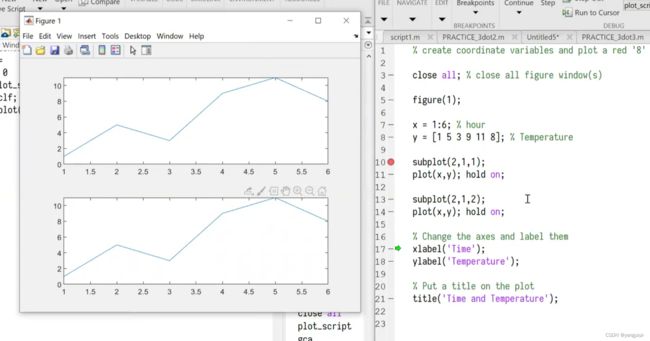
subplot()
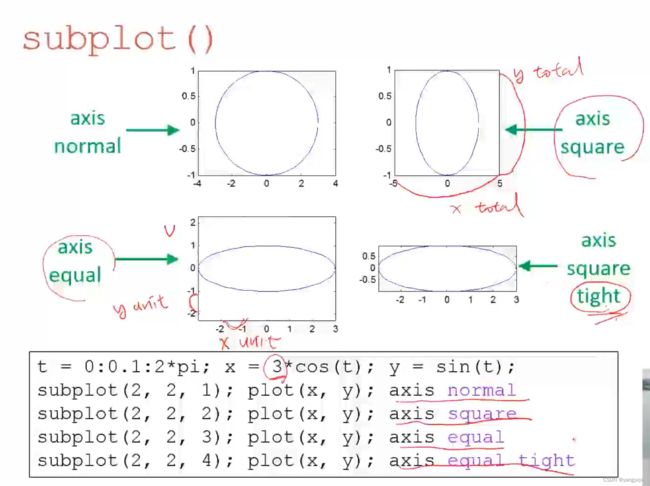
练习1:
n = 2;
for i = 1:2
x = linspace(0,2*pi,20*i);
y = sin(x);
subplot(1,n,i); # 1行n列
plot(x,y,'ko-');
xlabel("x");
ylabel("y");
end
练习2:
subplot(2,2,1)
subplot(2,2,3)
subplot(2,2,[2,4]) # 也等价于 subplot(1,2,2 )
练习3:
%%
figure(1)
n = 3;
x = 0:0.01:1;
for i = 1: n
y = exp(2^i*x);
%subplot(2,2,i+1);
plot(x,y);
hold on;
end
xlabel("x");
ylabel("exp(2^ix)");
legend("exp(2^0x)","exp(2^1x)","exp(2^2x)");
上面的缺点:图例的个数需要自己手动添加
改进:使用plot中的字段:DisplayName+legend(“show”)
%%
figure(1)
n = 3;
x = 0:0.01:1;
for i = 1: n
y = exp(2^i*x);
%subplot(2,2,i+1);
plot(x,y,'LineWidth',5,'DisplayName','exp(2^ix)');
hold on;
end
xlabel("x");
ylabel("exp(2^ix)");
legend("show");
上面的缺陷一:图例的内容没有改变;
使用num2str函数进行字符串的拼接
点击跳转到 - 拼接的使用
num2str(num,“%6.2f”);进行格式化输出
%%
figure(1)
n = 3;
x = 0:0.01:1;
for i = 1: n
y = exp(2^i*x);
%subplot(2,2,i+1);
plot(x,y,'LineWidth',5,'DisplayName',['exp(2^' num2str(i) 'x)']);
%等价于 plot(x,y,'LineWidth',5,'DisplayName',+"exp(2^"+ num2str(i)+ "x)"]);
hold on;
end
xlabel("x");
ylabel("exp(2^ix)");
legend("show");
标准文本(x轴上)
>> set(gca,'xtick',1:8:length(x),'xticklabel',TextData(1:8:59)) %将文本标注在x轴上，每个8个标准一次
柱状图
- bar(1:10,randi([1,10],[1,10]))
三维图的绘制
第一步:需要先绘制网格点
第二步:使用mesh绘图
>> fh = @(x,y)y.*sin(x) + x.*cos(y);
>> x = 0:pi/30:2*pi;
>> y = 0:pi/30:2*pi;
>[xi,yi] = meshgrid(x,y); % 生成网格采样点的函数
>>> z = fh(xi,yi);
>> mesh(xi,yi,z)
语句
if
练习1:
x = 100;
if x < -1
y = 1;
end
x = -2;
if x < -1
y = 1;
else
if x <=2
y = x^2;
else
y = 4;
end
end
x = -2;
if x < -1
y = 1;
elseif x <=2
y = x^2;
else
y = 4;
end
练习2:
信息：
>> whos
Name Size Bytes Class Attributes
matrix 2x3 48 double
v 1x1 8 double
vector 1x4 32 double
fundargtype([1 2 ; 12 2])
% 判断变量的类型
fundargtype([1;1;1])
% 判断变量的类型
function outtype = fundargtype(inputarg)
[size1,size2] = size(inputarg);
if size1 == 1
outtype = "是变量";
elseif size2 >1
outtype = "是行向量";
elseif size1 > 1 && size2 ==1
outtype = "是列向量"
else
outtype = "是矩阵";
end
end
switch numGrade
case 10
letGrade = 'A';
case 9
letGrade = 'B';
case 8
letGrade = 'C';
end
for
练习1：
for i =1:5
array(i) = i;
end
n =6 ;
array = NaN(n,1); %实现设置变量的空间
for i =1:5
array(i) = i;
end
上面的两个会使matlab执行效率相差很多
while
- 练习1:
解法一:
一批实验数据,-99之前的数据都是有效，请找出有效的数据
load data.dat;
i = 1;
while data(i) ~= -99
i = i + 1;
end
validData = data(1:i-1);
解法二:
load data.dat;
i = find(data == -99,1,'first');
.....
函数
函数表示
使用M文件
匿名函数
分段函数
>> fh = @(x)exp(x.^2).*(x<=2)+80./(4-sin(16*pi*x)).*(x>2)
```perl
1. 函数名最好和文件名一致
```perl
function area = calcarea(rad)
area = pi .* rad ;
end
matlab书写函数时，应该十分在意是否可以接受向量，一般可以接受标量时也可以接受向量:即使用点运算----为了批量进行运算
2. 当使用函数名作为文件名来存储函数时，此函数作为公共函数，在command line中可以访问到，但是在脚本中书写时只是作为局部函数，不能在command line中使用
3. hold on 是指上是 hold(“on”)
4. save file.bat mydata -ascii 等价于:save(“file.bat”," mydata"," -ascii")
function [par1,par2] = area(r)
par1 = ...;
par2 = ....;
end
- 当返回值有多个时，但是我使用该函数只关注于某个返回值，这时可以将不需要的返回值默认为
~即这样使用:[~,c] = area(4) - 当没有返回值时,这样定义:
function print(m) end - 关键字:
persistant相当于c语言中static在函数中的作用
function test
persistent count1;
disp("_________");
if isempty(count1)
count1 = 0;
end
count1 = count1 + 1;
disp(count1); # 执行一次 +1一次
end
- 关键字
global
function test
global count1; //去全局变量中去找
count1 = count1 + 1;
disp(count1);
end
- 关键字:nargin
function vol = calcarea(par1,par2,par3)
if nargin == 1
disp("参数个数是1");
elseif nargin == 2
disp("参数个数是2");
else
disp("参数个数是多个");
end
- nargout
- 函数句柄:
>> f = @(x) exp(-2*x)
f =
包含以下值的 function_handle:
@(x)exp(-2*x)
>> f(1)
ans =
0.1353
可变输入变量
function [area,circum] = practical(varargin) % varargin会将输入的参数加入到一个Cell结构中
rad = varargin{1};
if nargin == 2 %nargin 表示参数的数量
unit = varargin{2};
if unit == 'i'
rad = rad / 2;
end
end
area = pi * rad .^2;
circum = 2 * pi *rad;
end
------------------
function [area,circum] = practical(a1,varargin)
第一个参数给a1其余的付给varargin
练习二
function sersum = practical(r,varargin) % varargin会将输入的参数加入到一个Cell结构中
if nargin == 1
disp("只有一个变量");
n = randi([5,30]);
elseif nargin ==2
disp("只有两个变量");
n = varargin{1};
else
error('expecting 1 or 2 input variable.');
end
sersum = 1 + sum(r .^(1:n));
end
可变输出变量
function [type,varargout] = practical() % varargin会将输入的参数加入到一个Cell结构中
if nargout == 1 % 当调用想要一个变量时
type = '变量1'
varargout{1} = 1
elseif nargout == 2
type = '变量1 变量2'
varargout{1} = 1
varargout{2} = 2
elseif nargout == 3
type = '变量1 变量2 变量3'
varargout{1} = 1
varargout{2} = 2
varargout{3} = 3
end
end
---------------------
>> a = practical()
type =
'变量1'
varargout =
1×1 cell 数组
{[1]}
a =
'变量1'
>> [a b] = practical()
type =
'变量1 变量2'
varargout =
1×1 cell 数组
{[1]}
varargout =
1×2 cell 数组
{[1]} {[2]}
a =
'变量1 变量2'
b =
1
>> [a b c] = practical()
type
'变量1 变量2 变量3'
varargout =
1×1 cell 数组
{[1]}
varargout =
1×2 cell 数组
{[1]} {[2]}
varargout =
1×3 cell 数组
{[1]} {[2]} {[3]}
a =
'变量1 变量2 变量3'
b =
1
c =
2
Matlab小技巧
- 运行程序出错时，停在出错的地方
练习1：
function outputArg1 = conevol(radius,height)
outputArg1 = pi * radius .^2 .* height;
end
- 小的探究:连接字符串
[]和+,单引号和双引号的区别
name为拼接的a标签的锚点
double_add = "你好呀" + num2str(2)+"你好呀"
double_add = "你好呀2你好呀"
double_array = ["你好呀" num2str(2) "你好呀"]
double_array = "你好呀" "2" "你好呀"
single_add = '你好呀' + num2str(2)+'你好呀'
single_add = 40690 45868 43186
single_array = ['你好呀' num2str(2) '你好呀']
single_array = '你好呀2你好呀'
Name Size Bytes Class Attributes
double_add 1x1 150 string
double_array 1x3 258 string
single_add 1x3 24 double
single_array 1x7 14 char
总结:拼接字符串:1. 使用双引号相加 或者 2. 使用单引号和[]
3. string和char差异
字符变量可以被索引，而字符串变量不可以被索引。因此字符变量可以被当做一个由字符组成的一维向量。string是标量而char类型的字符串是矢量。将string转化为char型，string_atr{1}或者char(string_atr)
''和""中的空字符串
>> isempty([])
ans =
logical
1
>> isempty('')
ans =
logical
1
>> isempty("")
ans =
logical
0
- 效率问题
matlab中的统计时间的函数,tic....toc中
tic;
v = rand(1,3);
for i = 1:length(v)
v(i) = v(i) * 2;
end
toc;
上面的是没有效率（循环要小心运用可以使用向量运算尽量避免使用循环），修改如下
tic;
v = 3 .* v;
toc;
- 预先设置空数组使用NaN
v = NaN(1,10) //预先定义一个·一维数组
- 逗号分割的列表
fprintf(‘%f’,pi,pi) === fprintf(‘%f %f’,pi,pi)
[数据]：将逗号分割的列表转化为数组的形式
{数据}:将逗号分割的列表转化为cell 数组
例如:
cell = {1,2,3}
cell(1)
->{[1]}
cell{1}
->1
cell{1:2} 这个返回的就是逗号分割的列表
->1
->2
{cell{1:2}}将产生的逗号分割的列表有转化为cell
例如:利用逗号分割的列表来遍历结构体数组
for i =1:3
fprintf("%d",packages(i).cost);
end
等价于：
fprintf("%d",packages.cost)
>> [b1,b2,b3] = a1,a2,a3
等号右侧的输出数目不足，不满足赋值要求
上面操作错误的原因是:matla将遇到的第一个逗号当做一个语句的结束
正确操作:
a,b = cell{1:2} 按道理左右两边都是逗号分割的列表但是发现这样会报错
上面操作错误的原因是:matla将遇到的第一个逗号当做一个语句的结束
C = {a1,a2,a3}
[b1,b2,b3] = C{:}
上面就等价于:[b1,b2,b3] = deal(a1,a2,a3)
一般可以用于提取结构体中的数据
package(1).cost = 1
>> package(2).cost = 2
>> package(3).cost = 3
>> package.cost
ans =
1
ans =
2
an =
3
>> a = package.cost
a =
1
>> a = [package.cost]
a =
1 2 3
function [a,b] = test(c,d)
a = c+d
b = c-d
end
当调用时:
tmp = test（1,2）
只会赋值第一个
正确:
[t1,t2] = tets(1,2)
a1=1
a2=2
a3=3
[b1,b2,b3] = a1,a2,a3 error matlab解析时以逗号结束
应该:
cell = {a1,a2,a3}
[b1,b2,b3] = cell{: }
更加方便的方法：deal有分派的意思,可以产生逗号分割的列表
[b1,b2,b3] = deal(a1,a2,a3)
有趣的事:
[cell{:}] 将逗号分割的列表转化为数组
b = packages.cost
b =19.9900
>> b = [packages.cost]
b =19.9900 5.9900 11.1100
画图时:
逗号分割的列表一般用于函数传参时:
x = -pi:pi/10:pi;
y1 = sin(x);
y2 = cos(x);
y3 = sinh(x);
Dec = {'o-','LineWidth',3,'MarkerEdgeColor','r','MarkerFaceColor','y'};
figure(1);clf;hold on;
plot(x,y1,Dec{:});
plot(x,y2,Dec{:});
plot(x,y3,Dec{:});
模块化编程
应用
矩阵有关运算
-
zeos(1,n), ones(1,n),
-
服从均匀(0-1)分布rand(1,n) 服从标准正态分布randn(1,n) 服从均匀分布([start-end])randi([start,end],行数，列数) 生成等差数列
-
linspace(start,end,number)
-
[m,n] = size(V),length(V) -
求矩阵的秩:rank(v)
-
判断三个向量是否相关: 将三个向量构造成一个矩阵，然后判断矩阵的秩
>> x
x =
1 1 1
>> y
y =
-1 2 1
>> z
z =
2 2 2
>> v
v =
1 1 1
-1 2 1
2 2 2
>> rank(v)
ans =
2
- 求向量余弦
>> v1 = randn(1,3)
v1 =
0.5377 1.8339 -2.2588
>> v2 = randn(1,3)
v2 =
0.8622 0.3188 -1.3077
>> cosa = (v1-v2)/norm(v1-v2) % 计算两个向量的方向余弦
cosa =
-0.1785 0.8333 -0.5232
- 向量的内积
几何意义:一个向量在另外一个向量上的投影长度，向量内积代表两个向量对应坐标值相乘后相加，得到的是一个数，数值上等于两向量长度积乘以夹角的余弦。
dot(A,B) = sum(A .* B) - 向量的叉积
cross(x,y) - 混合积
dot(cross(a,b),c ) - 求行列式的值
det(A) - 点到平面的距离
- 求解方程的解
1. 通过 A的逆矩阵 * b
2. 也可以使用克拉默法则
% 通过逆矩阵
>> A = [1 2 3;1 4 9;1 8 27]
A =
1 2 3
1 4 9
1 8 27
>> b = [5;-1;6]
b =
5
-1
6
>> A_ = inv(A)
A_ =
3.0000 -2.5000 0.5000
-1.5000 2.0000 -0.5000
0.3333 -0.5000 0.1667
>> A_ * b
ans =
20.5000
-12.5000
3.1667
% 通过克莱默法则
>> A_x1 = [b,A(:,2:3)]
A_x1 =
5 2 3
-1 4 9
6 8 27
>> x1 = det(A_x1)/det(A)
x1 =
20.5000
-
求矩阵的特征值
eig(A)
-
矩阵的迹
trace(A)
迹，特征值,行列式都是相似不变量。与坐标基变换无关 -
正定矩阵
-
检查矩阵的误差
norm(产生的矩阵-原来的矩阵,'fro')观察其范数 -
矩阵的分解
方法一：
>> A= gallery('lehmer',5) % 得到一个正定矩阵
A =
1.0000 0.5000 0.3333 0.2500 0.2000
0.5000 1.0000 0.6667 0.5000 0.4000
0.3333 0.6667 1.0000 0.7500 0.6000
0.2500 0.5000 0.7500 1.0000 0.8000
0.2000 0.4000 0.6000 0.8000 1.0000
>> D = chol(A)
D =
1.0000 0.5000 0.3333 0.2500 0.2000
0 0.8660 0.5774 0.4330 0.3464
0 0 0.7454 0.5590 0.4472
0 0 0 0.6614 0.5292
0 0 0 0 0.6000
>> D'*D
ans =
1.0000 0.5000 0.3333 0.2500 0.2000
0.5000 1.0000 0.6667 0.5000 0.4000
0.3333 0.6667 1.0000 0.7500 0.6000
0.2500 0.5000 0.7500 1.0000 0.8000
0.2000 0.4000 0.6000 0.8000 1.0000
方法二:
>> A = gallery('fiedler',5) %得到一个对称阵
A =
0 1 2 3 4
1 0 1 2 3
2 1 0 1 2
3 2 1 0 1
4 3 2 1 0
>> [V,D] = eig(A)
V =
0.6015 -0.4354 0.3717 0.1662 0.5317
0.3717 0.2856 -0.6015 -0.5129 0.3942
0.0000 0.6765 -0.0000 0.6470 0.3517
-0.3717 0.2856 0.6015 -0.5129 0.3942
-0.6015 -0.4354 -0.3717 0.1662 0.5317
D =
-5.2361 0 0 0 0
0 -1.7304 0 0 0
0 0 -0.7639 0 0
0 0 0 -0.5578 0
0 0 0 0 8.2882
>> A_ = V*D*V'
A_ =
0.0000 1.0000 2.0000 3.0000 4.0000
1.0000 0.0000 1.0000 2.0000 3.0000
2.0000 1.0000 0.0000 1.0000 2.0000
3.0000 2.0000 1.0000 0.0000 1.0000
4.0000 3.0000 2.0000 1.0000 0.0000
方法三:
三角分解(A必须可逆)
>> [L,U] = lu(A)
L =
0 1.0000 0 0 0
0.2500 -0.7500 1.0000 0 0
0.5000 -0.5000 0 1.0000 0
0.7500 -0.2500 0 0 1.0000
1.0000 0 0 0 0
U =
4 3 2 1 0
0 1 2 3 4
0 0 2 4 6
0 0 0 2 4
0 0 0 0 2
>> L*U
ans =
0 1 2 3 4
1 0 1 2 3
2 1 0 1 2
3 2 1 0 1
4 3 2 1 0
方法四:
QR分解
没有限制
>> [Q,R] = qr(A)
Q =
0 0.7746 0.4781 0.3646 -0.1961
-0.1826 -0.5164 0.8367 -0.0000 0.0000
-0.3651 -0.2582 -0.2390 0.8619 -0.0000
-0.5477 -0.0000 -0.1195 -0.2652 -0.7845
-0.7303 0.2582 -0.0000 -0.2320 0.5883
R =
-5.4772 -3.6515 -2.1909 -1.4606 -1.8257
0 1.2910 1.5492 1.2910 1.0328
0 0 1.6733 2.8685 3.8247
0 0 0 1.7238 2.9172
0 0 0 0 -1.5689
方法五:SVD分解
- 线性方程组的求解
function [x,y] = practical(A,b)
% A为系数矩阵，b为右端向量。x为唯一解或者特解,y是基础解
y = []
if nargin < 2
disp('请你输入系数矩阵和右端向量')
return
end
[m,n] = size(A);
if norm(b) > 0 % 非齐次 norm求解其范数
if rank(A) == rank([ A b]) % 有解
if rank(A) == n
disp("该非齐次方程组有唯一解");
x = A\b;
return
else
disp("该非齐次方程组有无穷个解===");
x = A\b; % 特解
y = null(A,'r');
return
end
else
disp('该非齐次方程组无解,其最小二乘解:')
x = A\b;
return
end
else %齐次方程
if rank(A) == n %该齐次方程组有唯一解
disp("齐次方程组有唯一解")
x = zeros(m,1);
return
else %该齐次方程组有无穷个解
disp("齐次方程组有无穷个解")
y = null(A,'r');
return
end
end
end
- 多项式的表示与运算
在matlab多项式用一个行向量来表示,系数按照未知数的次数降序来排列
>> p = [1 2 3 3]
p =
1 2 3 3
>> fx = poly2sym(p)
fx =
x^3 + 2*x^2 + 3*x + 3
- 多项式的乘法：系数向量之间的卷积运算
- 多项式的除法:使用反卷积函数deconv来实现
>> fx1 = [3 -5 2 7 5 6]
fx1 =
3 -5 2 7 5 6
>> fx2 = [3 5 -3]
fx2 =
3 5 -3
>> fx3 = [0 0 0 3 5 -3]
fx3 =
0 0 0 3 5 -3
>> fx1 + fx3
ans =
3 -5 2 10 10 3
>> poly2sly(fx1+fx2) % 加法和减法维数必须一致
矩阵维度必须一致。
>> poly2sym(fx1+fx3)
ans =
3*x^5 - 5*x^4 + 2*x^3 + 10*x^2 + 10*x + 3
>> conv(fx1,fx2) % 乘法和除法 不必要维数一致
ans =
9 0 -28 46 44 22 15 -18
>> [p,q] = deconv(fx1,fx2)
p =
1.0000 -3.3333 7.2222 -13.0370
q =
0 0 0 0 91.8519 -33.1111
polyvalm(A,p)将矩阵A带入求值
polyder(A)
- 数据拟合
- 数据拟合后的误差分析
练习:
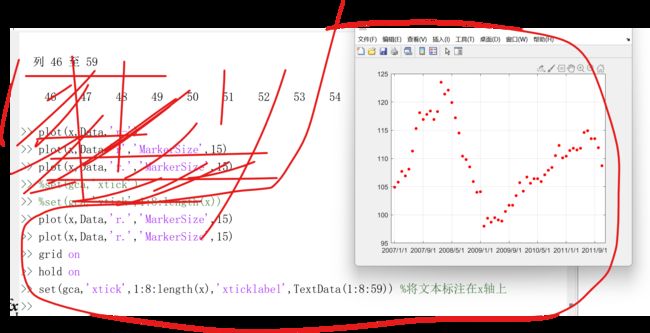
%从xls表格中提取数据
[Data,TextData] = xlsread('examp41',1,'B3:C61')
x = 0:59
plot(x,Data,'r.','MarkerSize',15)
%现在想把时间设置在x轴上，
set(gca,'xtick',1:8:length(x),'xticklabel',Textdata(1:8:59))
xlabel('时间')
ylabel('食品零售指数')
title("万固")
x = x' %为了和Data数据格式相同都是列向量
[p4,s4,mu4] = polyfit(x,Data,4)
y4 = polyval(p4,x,s4,mu4);
hold on
plot(x,y4,'k:','LineWidth',1.5) %画出拟合的曲线
- 非线性拟合
function y = practical(beta,x) % varargin会将输入的参数加入到一个Cell结构中
a = beta(1);
b = beta(2);
y = a + (0.49-a).*exp(-b*(x-8));
end
beta0 = [0 0]; % 自己猜测的值
beta = nlinfit(x,y,'nlinfun',beta0)
yp = practical(beta,x); %根据拟合出来的函数，得到y值
- 一维数据插值
function practical() % varargin会将输入的参数加入到一个Cell结构中
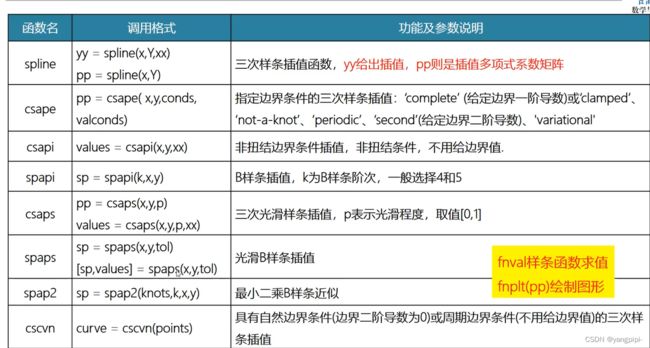
x = 0:4*pi
y = sin(x) % 已知数据值
xi = 0:0.1:4*pi % 待插入点
methods = {'nearst','linear','spline','cubic'};
strtitle = {'method=nearst','method=linear','method=spline','method=cubic'};
for i = 1:4
yi = interp1(x,y,xi,methods{1});
subplot(2,2,i);
plot(x,y,'ro','MarkerFaceColor','r'); % 已知数据离散点绘图
hold on
grid on
plot(xi,yi,'b--','LineWidth',1.5); % 绘制插入点曲线
title(strtitle(i));
end
end
案例二:
x = linspace(0,8.534,13);
y = [0,0.914,5.06,7.772,8.717,9.083,9.144,9.083,8.992,8.687,7.376,2.073]
xi = 0:0.001:8.534
plot(xi,yi,'r-','LineWidth',1.5)
yi = spline(x,y,xi);
- 高维插值
mesh(x,y,z)可以绘制三维图网格图
数学相关
函数极值
一元函数
练习1:
>> fh = @(x)x-1./x+5;
>> fplot(fh,[-10,10],'b-','LineWidth',1.5)
>> grid on
>options = optimset('Display','iter','PlotFcns',@optimplotfval);
>options = optimset('Display','iter','PlotFcns',@optimplotfval,'TolX',1e-6);
%精度:
1.000000e-06
练习2:
fh = @(x)2*exp(-x).*sin(x);
options = optimset('Display','iter','PlotFcns',@optimplotfval,'TolX',1e-6);
[x,fval_min,exitflag,output] = fminbnd(@fx,-2,3,options)
fplot(fh,[0,8],'LineWidth',1.5) % 绘制函数图像
axis([-0.5,8.5,-0.1,0.75]) % 修改修改坐标轴的取值
求函数的极大值通过极小值来求，通过在定义的函数fh前添加'-'负号
fh = @(x)-2*exp(-x).*sin(x);
[x,fval_max,exitflag,output] = fminbnd(@fx,-2,3,options)
fval_real_max = fval_max
多元函数
练习1:（使用fminsearch（））
% 注意函数中点乘的运算
fh = @(x,y)(x.^2-2.*x).*exp(-x.^2-y.^2-x.*y)
fsurf(fh,'ShowContours','on') % 为观察到极值的大致范围,显示出等高线
%但是采用fsurf绘制出的等高线不清晰，那么采用下面的方法
[x,y] = meshgrid(-5:0.1:5,-5:0.1:5)
z = fh(x,y);
mesh(x,y,z)
[c,h] = contour(x,y,z) % 绘制出等高线
set(h,'ShowText'，'on'); %在等高线上标出点
%%%%%%%%%所有从等高线得出初值范围
%注意:
定义的函数中的参数使用一个
fh = @(x)(x(1).^2-2.*x(1)).*exp(-x(1).^2-y(2).^2-x(1).*y(2))
[x,fval_min,exitflag,output] = fminsearch(fh,[-0.5,0.5],options)
注意求最大值时,只需修改定义函数前添加负号，‘-’
fh = @(x)-(x(1).^2-2.*x(1)).*exp(-x(1).^2-y(2).^2-x(1).*y(2))
[x,fval_max,exitflag,output] = fminsearch(fh,[-1,0.5],options)
fval_max = -fval_max
函数求解
单变量函数求解(fzero)
练习1:
>> fh = @(t)sin(t).^2.*exp(-0.1*t)-0.5*abs(t);
>> fplot(fh,[-4,4],'b-','LineWidth',1.5) % 初始化画出图像观察其有几个根并且估计其根的范围
>>
>> grid on
>> hold on
>> fplot(@(t)0*t,[-4,4]) %在图中标注出x轴
>> % 分别求各点附近的根
>> [t1,y1] = fzero(fh,-2)
t1 =
-2.0074
y1 =
2.2204e-16
>> [t2,y2] = fzero(fh,-0.5)
t2 =
-0.5198
y2 =
0
>> [t3,y3] = fzero(fh,-0.5);
>> [t2,y2] = fzero(fh,-0.5);
>> [t3,y3] = fzero(fh,-0.1);
>> [t3,y3] = fzero(fh,0.1);
>> [t4,y4] = fzero(fh,0);
>> [t5,y5] = fzero(fh,2);
>> plot([t1,t2,t3,t4],[y1,y2,y3,y4],'co','MarkerFaceColor','c')
多变量函数求解(fsolve)
函数
function f = practical(v)
x = v(1);
y = v(2);
z = v(3);
f(1) = sin(x) + y + z.^2.*exp(x)-4;
f(2) = x + y.*z;
f(3) = x .* y .* z;
end
>> fh = @practical
>> options = optimoptions('fsolve','Display','none','PlotFcn',@optimplotfirstorderopt);
>> [x,fval] = fsolve(fh,[1,1,1],options)
x =
0.0005 -0.0002 1.9995
fval =
1.0e-06 *
-0.2636 0.1200 -0.2131
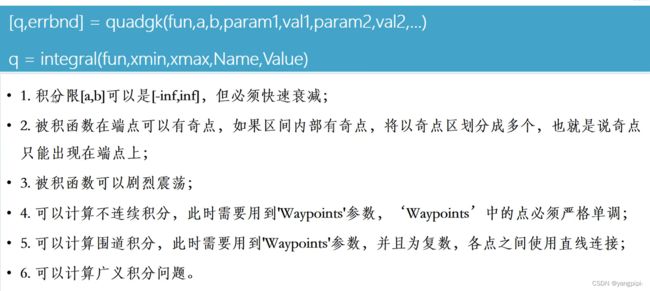
数值积分(定积分)
- 梯形法
- 辛普森法
- 牛顿-科特斯法
--------------------------求和问题
1. 矩形区域积分
>> fh = @(x)sin(x);
>> I1 = quad(fh,0,pi/2)
I1 =
0.999999997873119
>> I2 = quadl(fh,0,pi/2)
I2 =
0.999999999991747
>> I3 = quadgk(fh,0,pi/2)
I3 =
1.000000000000000
>> I3 = integral(fh,0,pi/2)
I3 =
1.000000000000000
练习2：
>> fh = @(x)exp(-0.5.*x).*sin(x+pi/6)
>> x = 0:pi/30:3*pi;
>> y = fh(x);
>> h = area(x,y);
>> %area(X,Y)绘制Y对X的图，并填充0和Y之间的区域。
>> h.FaceColor = [0 0.75 0.75]
>> hold on;grid on;
>> fplot(fh,[0,3*pi],'r-','LineWidth',1.5);
>> axis([-0.5,3*pi+0.5,-0.2,0.8]);
>> L1 = integral(fh,0,3*pi)
L1 =
0.900840787818886
>> L2 = integral(fh,0,3*pi,'RelTol',1e-8,'AbsTol',1e-15)
L2 =
0.900840787818886
2. 具有特殊形式的被积函数积分问题
- 广义积分
- 含参积分
- 含奇点积分
- 高震荡积分
- 不连续积分
- 分段积分
"Waypoints'通过指定不连续点的位置，在被积函数的不连续点附近高效求积分。
练习1：
>> fh = @(x)exp(x.^2).*(x<=2)+80./(4-sin(16*pi*x)).*(x>2)
fh =
包含以下值的 function_handle:
@(x)exp(x.^2).*(x<=2)+80./(4-sin(16*pi*x)).*(x>2)
>> l1 = integral(fh,0,4,'AbsTol',1e-10,'Waypoints',[2]) %含奇点
l1 =
57.764450125048512
>> l2 = quadgk(fh,0,4,'AbsTol',1e-10,'Waypoints',[2]) %含奇点
l2 =
57.764450125048512
>>
3. 二重积分(矩形区域)
>> fh = @(x,y)exp(-x.*2/2).*sin(x.^2+y);
>> q = integral2(fh,-2,2,-1,1,'Method','iterated','AbsTol',1e-8,'RelTol',1e-12)
q =
4.317240405304355
4. 三重积分
练习1:
>> fh = @(x,y,z)4*x.*z.*exp(-x.^2.*y-z.^2);
>> l2 = integral3(fh,0,1,0,pi,0,pi,'AbsTol',1e-8,'RelTol',1e-12)
l2 =
1.732762223028910
5. 向量化积分
>> fh = @(x,n)besselk(0,(1:n).^2*x*sqrt(x)+1);
>> sf = quadv(@(x)fh(x,10),0,1)
sf =
列 1 至 4
0.264618867193065 0.126095847282322 0.073745970190692 0.050252773366313
列 5 至 8
0.037320330119224 0.029266365264176 0.023828895725781 0.019942420548401
列 9 至 10
0.017043934673509 0.01480995352232
或者使用integral3
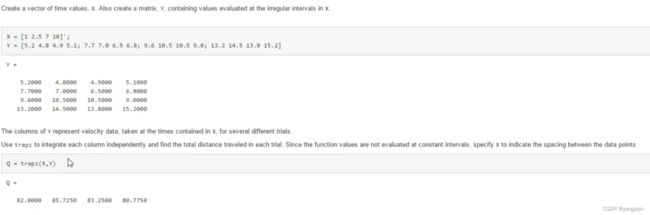
6. 离散数据积分
两个例子:
>> x = 0:pi/100:pi/2;
>> y = sin(x);
>> S1 = trapz(x,y)
S1 =
0.999917751943722
>> x = -3:0.01:3;
>> y = -5:0.01:5;
>> [X,Y] = meshgrid(x,y);
>> [X,Y] = meshgrid(x,y);%生成网格点
>> Fval = X.^2 + Y.^2;
>> %trapz先对x求积分以生成列向量。然后，y上的积分可将列向量减少为单个标量。
>>
>> V = trapz(y,trapz(x,Fval,2))
V =
6.800020000000000e+02
mesh(X,Y,Fval)
参数中可以直接用矩阵
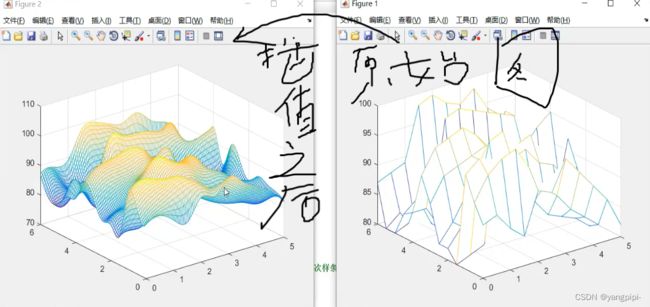
>> x=[0,2,4,5:9,10.5,11.5,12.5,14,16:24];
>> y=[20,25,30,35,40,50,155,92,60,62,60,43,59,140,120,68,60,80,55,65,20];
>> xi = 0:1/60:24; % h缩小,数据插值
>> yi = spline(x,y,xi);
>> plot(xi,yi,'r-','LineWidth',1.5)
>> grid on;
>> hold on;
>> plot(x,y,'b*','LineWidth',1.5)
>> tf2 = trapz(xi,yi)
tf2 =
1.463326739891108e+03
>> tf1 = trapz(x,y)
tf1 =
1.483750000000000e+03
练习2:
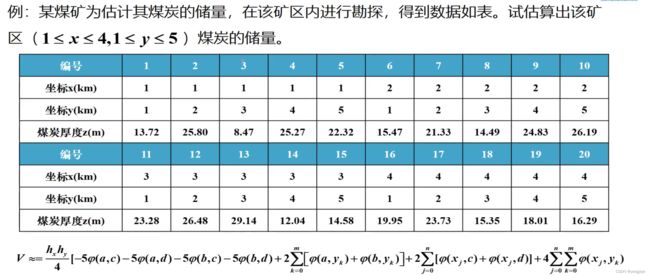
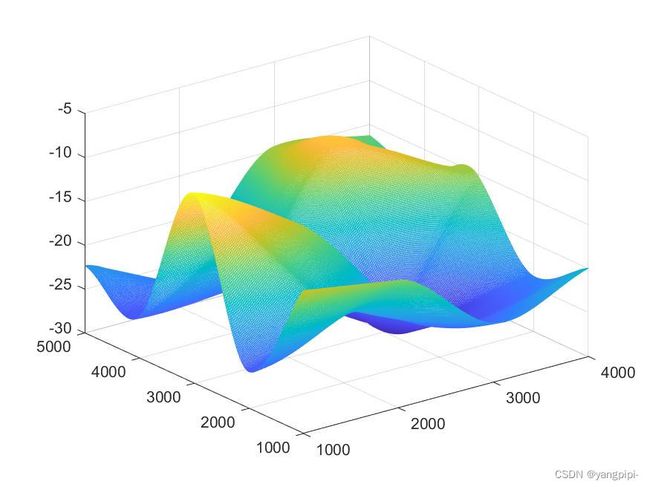
>> X=[1 1 1 1 1 2 2 2 2 2 3 3 3 3 3 4 4 4 4 4]*1000;
>y=[1 2 3 4 5 1 2 3 4 5 1 2 3 4 5 1 2 3 4 5 ]* 1000;
>Z=-[13.72 25.80 8.47 25.27 22.32 15.47 21.33 14.49 24.83 26.19 23.28 26.48 29.14 12.04 14.58 19.95 23.73 15.35 18.01 16.29];
>> hx = 1000:10:4000;
>> hy = 1000:10:5000;
>> [xi,yi] = meshgrid(hx,hy);
>> %插值的方法
>> z = griddata(x,y,Z,xi,yi,'cubic');
>> z = griddata(X,y,Z,xi,yi,'cubic');
>> mesh(xi,yi,z)
>> V = trapz(hy,trapz(hx,z,2))
V =
-2.469468142963782e+08
7. 一般区域二重积分
tic:计算时间
1.练习
>> y = @(x,y)exp(sin(x).*log(y));
>> q1 = integral2(y,10,20,@(x)5*x,@(x)x.^2,'Method','iterated','AbsTol',1e-15,'RelTol',1e-10)
q1 =
3.361859178681768e+04
8. 一般区域三重积分
>> ymin = @(x)sqrt(x);
>> ymax = @(x)2*x;
>> zmin = @(x,y)x.*y;
>> zmax = @(x,y)2*x+y;
>> fh = @(x,y,z)x.*sin(y+z).*(x+z.^2);
>> I = integral3(fh,1,2,ymin,ymax,zmin,zmax)
I =
12.653057240716713
fh = @(y)2*y*exp(-y.^2).*(integral(@(x)exp(-x.^2)./(y.^2+x.^2),-1,1)).^2
fh =
包含以下值的 function_handle:
@(y)2*y*exp(-y.^2).*(integral(@(x)exp(-x.^2)./(y.^2+x.^2),-1,1)).^2
>> I = integral(fh,0.2,1,'ArrayValued',true)
I =
10.213463733952983
9. 一般区域n重积分
nlntegrate(fun,low,up)
function f = nIntergrate(fun,low,up)
% f,返回值，n重积分积分结果
% fun,是被积函数字符串形式；
% low 存储从外到内各重积分的积分下限函数；
% up 存储从外到内各重积分的积分上限函数（都是字符串形式）
% 为了保证函数正常运行，low和up内的函数遵循如下原则：设积分重数为m，最内层
% 到最外层积分变量依次以xm,...x2,x1来表示（规定只能以这样的顺序而且只能字母x代表变量）
% 最内层的变量积分范围不管是否和x(m-1)相关都要求出现x(m-1)，不是的可以在积分范围
% 后加上‘+0*x(m-1)’等形式的字符串，依次类推，次内层要求x(m-2)出现，一直到最
% 外层，最外层才是常数
%
% 参考书籍：MATLAB高效编程技巧与应用：25个案例分析 91页
N = length(low);
fun = vectorize(fun);
if verLessThan('MATLAB','7.8')
expr = GenerateExpr_quadl(N);
else
if mod(N,2) == 0
expr = GenerateExpr_quad2d(N);
else
expr = ['quadl(@(x1) arrayfun(@(x1)',GenerateExpr_quad2d(N-1),',x1),',low{1},',',up{1},')'];
end
end
%============================================================
% 主要利用quadl函数递归构造求解表达式，适用于R2009a以前的版本
%============================================================
function expr = GenerateExpr_quadl(n)
if n == 1
expr = ['quadl(@x',num2str(N),')',fun,',',low{N},',',up{N},')'];
else
expr = ['quadl(@(x',num2str(N-n+1),') arrayfun(@(x',num2str(N-n+1),')',GenerateExpr_quadl(n-1),',x',num2str(N-n+1),'),',low{N-n+1},',',up{N-n+1},')'];
end
end
%============================================================
% 主要利用quad2d函数递归构造求解表达式，适用于R2009a以及以后的版本
%============================================================
function expr = GenerateExpr_quad2d(n)
if n == 2
expr = ['quad2d(@(x',num2str(N-1),',x',num2str(N),')',fun,',',low{N-1},',',up{N-1},',@(x',num2str(N-1),')',low{N},',@(x',num2str(N-1),')',up{N},')'];
else
expr = ['quad2d(@(x',num2str(N-n+1),',x',num2str(N-n+2),')','arrayfun(@(x',num2str(N-n+1),',x',num2str(N-n+2),')',GenerateExpr_quad2d(n-2),',x',num2str(N-n+1),',x',num2str(N-n+2),'),',low{N-n+1},',',up{N-n+1},',@(x',num2str(N-n+1),')',low{N-n+2},',@(x',num2str(N-n+1),')',up{N-n+2},')'];
end
end
f = eval(expr);
end
在这里插入代码片
由于是字符串所以就不用在乎是否点乘形式
··
>> fun = 'exp(x1*x2*x3*x4)';
>> up = {'1','0*x1+1','0*x2+1','0*x3+1'};
>> low = {'0','0*x1','0*x2','0*x3'};
>> f1 = nlntegrate(fun,low,up);
>> fun2 = 'x1*x2*x3';
>> up = {'2','2*x1','2*x1*x2'};
>> low = {'1','x1','x1*x2'};
>> f2 = nIntergrate(fun2,low,up)
f2 =
1.792968750000302e+02
>> fun4 = 'sqrt(x1*x2)*log(x3)+sin(x4/x2)';
>> up = {'2','3*x1','2*x1*x2','x1+2*x1*x3'};
>> low = {'1','x1','x1*x2','x1+x1*x3'};
>> f4 = nIntergrate(fun4,low,up)
f4 =
1.502515543166793e+03
10. 蒙特卡洛计算n重积分
蒙特卡洛方法又称随机抽样法或统计试验方法
蒙特卡洛方法用于求积分时，与积分重数无关，这点非常重要。
虽然四维以下的积分用蒙特卡洛法效率可能不如传统的一些数值积分方法，但是维数高的时候，蒙特卡洛法比传统方法要有效的多，而且实现起来也非常容易。可以说，计算高维积分是蒙特卡洛方法最成功和典型的应用。
1. 基本的蒙特卡洛积分法
>> fhm = @(x)(x(:,1).^4-8*x(:,1).*x(:,2)+2*sin(x(:,2))-3);
>> n = 1000000; # % 随机生成一百万个点
>> x(:,1) = unifrnd(2,5,1,n); % 均匀分布的方法 1：n表示生成向量形式
>> x(:,2) = unifrnd(0,23,1,n); % 23 是 (2,5)之间取`x^2-2`的最大值
>> ind = (x(:,2) >=0 & (x(:,2)<=x(:,1).^2-2)); % 生成的点应该满足的关系
>> fhlm = (5-2)*(23-0)*sum(fhm(x(ind),:))/n;
>> fhlm = (5-2)*(23-0)*sum(fhm(x(ind,:)))/n
fhlm =
1.704821173857696e+03
2. 等分布序列的蒙特卡洛积分法
微分方程(组)的数值解
显
MATLAB绘图与可视化
