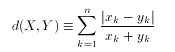本文版权属作者所有,转载需注明出处,谢谢
多种相似距离对比
多种相似距离对比
因某些原因需要对样本进行相似度方面的计算,对常见的几种距离公式进行了一系列实验。
距离公式:距离的衡量在相似度衡量中占据了重要的地位,不同的距离公式有其不同的应用场景,都是为了解决某类问题而诞生的,本文期望对这些距离公式能有个”0距离”的亲密接触。
目录
1. 欧氏距离
2. 切比雪夫距离
3. 曼哈度距离
4. 闵可夫斯基距离
5. 兰氏距离
6. COS余弦距离
1. 欧氏距离
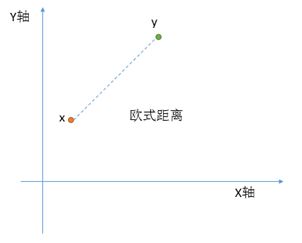
欧式来源于顶顶大名的欧几里得,那么自然会想到空间几何,以其名义命名的距离公式是初中就接触到的距离公式,在二维空间中其几何意义表示的两点之间的直线距离,有了这个你就应该知道,在这里它认为你的这两维量纲是一样的(X轴,Y轴),所以什么时候该用距离公式自己看着办罗。(注意:距离用虚线表示)。
附上代码(writen by R)
Euclidean <- function(x,y){
sqrt(sum((x-y)^2))
}
2. 切比雪夫距离
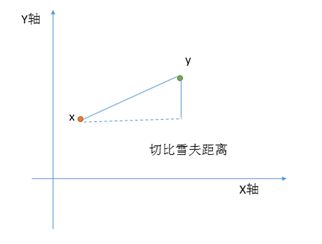
都说切比雪夫距离公式起源于国际象棋,我不想不懂装懂,国际象棋还真不记得怎么玩了,anyway,猜想应该是和某种策略相关的,根据公式来看,其将各维度上最大距离作为最终距离,可以看出该公式认为不同维度的量纲也是一致的。
Chebyshev <- function(x,y){
max(abs(x-y))
}
3. 曼哈度距离
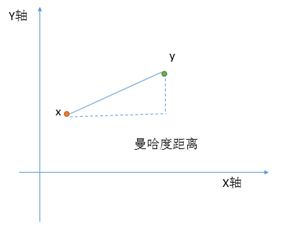
该公式来源于度量城市距离,因为城市一般为方形的街区建设,因此该公式本质上是度量从地图上某点x到某点y的街区距离,根据公式来看,其将各维度上所有距离和作为最终距离,可以看出该公式认为不同维度的量纲也是一致的。
Manhattan <- function(x,y){
sum(abs(x-y))
}
目录
1. 欧氏距离
2. 切比雪夫距离
3. 曼哈度距离
4. 闵可夫斯基距离
5. 兰氏距离
6. COS余弦距离
4. 闵可夫斯基距离
该距离公式应该被称为通用距离公式,其代表的是一组距离公式,当p=1的时候,其与曼哈度公式等价;当P=2的时候,其与欧氏距离等价;当p->无穷的时候,其与切比雪夫距离等价(后续进行简单证明)
因此可以说闵可夫斯基距离是定义了通用距离,这一组通过距离公式在多种相似距离对比(一)中进行过详细描述,他们都具有相同的特性,即认为变量的每个维度都具有同样的量纲维度,具体说明一下:
比如我们在空间坐标中存在二维向量 x(1,20),y(1,30),z(11,20),那么利用闵可夫斯基距离组公式组计算我们会发现sim(x,y)=sim(x,z)是始终成立的,仔细观察x与y的区别是第二维向量增加了10个单位,x与z的区别是第一维向量增加了10个单位,那么闵氏距离组认为,向量的每个维是一样的,因此其在不同的维度上的变换是等价的。这个是闵氏距离组的特点!
当你的向量的各个维度是有不同量纲时,即比如第一维代表身高,第二维代表体重,我们认为身高增加10cm决定不等同于体重增加10斤的时候,那么我们直接使用闵氏距离组公式来测量距离是不合适的。那么我如果硬是要用,该怎样fix这种量纲上的diff呢?这里介绍一种改进的方法可能会有用,但是不保证适用所有场景。
Minkowski <- function(x,y){
(sum((x-y)^p))^(1/p)
}
z-score标准化
该方法也比较简单,即将向量进行标准化,标准化公式为 x=(x-\mu )/\sigma,其中\mu为均值,\sigma为方差。假设两个n维向量a(x11,x12,…,x1n)与 b(x21,x22,…,x2n),那么将欧式距离进行标准化为: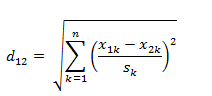
其中,sk为方差。将2换为p,开平方换为开P次方,那么即是标准闵氏距离公式。因为方差sk可以提到括号前面前面去看做一个常量,因此标准闵氏距离组公式也称为加权标准闵氏距离公式。
证明
前面提到当p->无穷的时候,闵氏距离等价于切比雪夫距离,这里给出简单证明思路,我们首先知道一个分数的指数,形如\frac{1}{k}^{n} ,当k>1,n趋于无穷时,其极限值趋于0。闵氏距离公式如下:
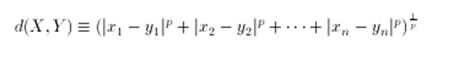
我们知道在绝对差值对|x-y|中存在最大的绝对差值对|xk-yk|,那么d(X,Y)/|xk-yk|,我们会得到n-1组值小于1的绝对差对,1组绝对值差等于1,那么当p趋于无穷时,d(X,Y)/|xk-yk|趋于1,即d(X,Y)=|xk-yk|。证明完毕。
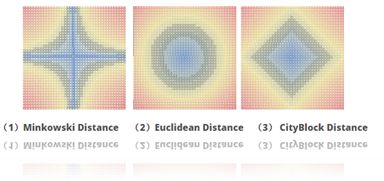
最后,附上闵氏距离,欧式距离,曼哈度距离的中心图
目录
1. 欧氏距离
2. 切比雪夫距离
3. 曼哈度距离
4. 闵可夫斯基距离
5. 兰氏距离
6. COS余弦距离
5. 兰氏距离
设X=(x1,x2,…,xn),Y=(y1,y2,…,yn)为空间中的两点,那么兰氏距离d(X,Y)的公式为
可以看出来,兰氏距离与前面几种距离的不同之处即是其已经处理了其量纲,比如当x=(30,3),y=(70,7),那么dis=|30-70|/100+|3-7|/10=0.4+0.4=0.8;当x=(40,4),y=(60,6)dis=|40-60|/100+|4-6|/10=0.2+0.2=0.4,可以看出兰氏距离对变量的各个维度进行了量纲统一处理,即类似于上文提到的z-score变换,目的是消除各维度量纲不一致引起的距离偏差。
在上文多种相似距离对比(二)中提到的一个case,x(1,20),y(1,30),z(11,20),其中用闵氏距离组公式计算出来sim(x,y)=sim(x,z),但通常而言,变量的各个维度有其不一样的现实意义,最好能够体现其不同,那么利用兰氏距离计算sim(x,y)=0.2,而sim(x,z)=10/21=0.48,可以看出两者有明显的diff,再仔细观察一下数据,sim(x,y)中起作用的变换是20到30的变换,而sim(x,z)中起作用的变换是1到11,兰氏距离认为1到11的变换要大于20到30的变换,这即是兰氏距离公式的核心思想。
6. COS余弦公式
设X=(x1,x2,…,xn),Y=(y1,y2,…,yn)为空间中的两点,那么余弦距离s(X,Y)的公式为
这里要强调的一点事余弦距离与以上几种的不同,余弦距离的几何意义是两个向量的夹角大小,是另外一种意义上的"距离”。因为其实在几何空间中进行定义,其对变量各维度也有量纲一致的要求。
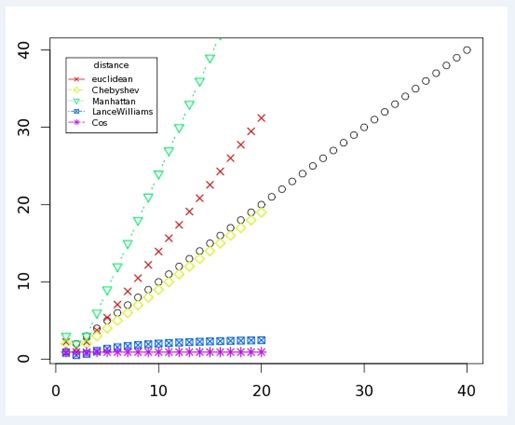
总结:下图是这6种距离在匀速增长各维度大小的时候,各种距离公式表示出来的趋势。可以看到虽然增长的幅度不一致,但是各距离公式在自己的幅度曲线下保持着稳定的变换,因为可以说这些距离公式是稳定的;还可以看出曼哈度距离增长最快,而余弦距离增长幅度最慢,切比雪夫距离保持着匀速增长;兰氏距离与余弦距离有类似的增长模式,增长曲线是”曲”的,而其余的曲线是”直”的。
相关链接
This entry was posted in 机器学习/数据挖掘/算法 by eletva. Bookmark the permalink.