GJK算法，碰撞检测（自学笔记，侵权删）
学哔哩哔哩《看似简单的复杂问题，奇怪而优雅的解决方式（GJK算法） | Reducible》——来自博主“我最会爬惹”笔记
一、凸形和凹形的基础概念
所有图形可以分成两种：凸形和凹形，如图1.1所示。
图1.1 凸形和凹形
凸形的性质是：
- 该形状上任意两点的连线，必然在这个形状内部，相较于凹形则更容易处理。
- 对于其形状上的每一个点，必然存在一个方向，使得该电视此方向上最远的点。即遍历该形状上所有有可能的方向并找到该方向上最远的点，则必然会得到形状上的每一个点。
而凹形则不遵守上述特性，所以在处理凹形的时候可以把它分割成多个凸形以简化计算，因此所有的形状间的相交判断都能转化为凸形的交集问题。
图1.2 凹形化为多个凸形
二、两个形状相交的相关特性
关于在两个形状相交判断中为何会出现“原点”概念的原因是如图2.1所示。当两个凸形相交，必然存在两个点（向量），他们的差是原点，而这也证明了两者间具有交集。
图2.1 2个形状相交与原点的关系
而上述这种“原点”的求解方法进一步提出了Minkowski和/差（Minkowski Sums/Differences ）的概念。
2.1 Minkowski和/差
Minkowski和：是将一个形状内部所有的点加到另一个形状内部所有的点上。而每个形状上的每个点都当做从原点出发的向量。
Minkowski差：是将一个形状内部所有的点与另一个形状内部所有的点相减。
图2.2 Minkowski和
图2.3 Minkowski差
Minkowski差还具有以下两个性质：
- 对于两个凸形的Minkowski差所得到的形状也是凸的；依据凸形的性质，这意味着任意两点的线必然存在于Minkowski差内；
- 两个形状相交，他们的Minkowski差必然会包含原点，即至少这两个形状至少有一个共同点（与图3的原理相同）；
所以两个形状的相交判定问题则变成了判断两个形状的Minkowski差中是否包含原点的问题。
选择两个凸形A和B中的三个点的差，构成一个三角形（这三个边必然在Minkowski差中）；当这个三角形中包含原点,则说明原点也必然存在于Minkowski差中，进而可以判断形状A和B相交。
图 2.4 三角形原点包含与凸形A、B相交的关系
因此，判定两个形状的相交问题进一步的简化为，是否能够在凸形A、B的Minkowski差中找到三个点以构成在原点附近的三角形（即包含原点的三角形），如图2.5所示。这个三角形被称作是单行（simplex）。
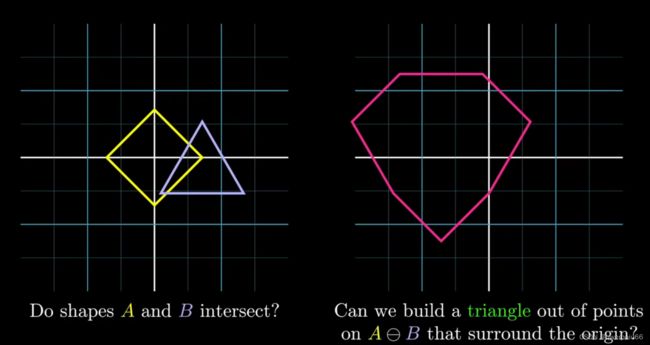图 2.5 相交与三角形问题简化
2.2 单行（simplex）
在不同维度下，单行的形状并不相同。在2D情况下，单行为一个三角形；而在3D情况下，单行则是一个四面体。
图2.6 单行的介绍
2.3 Support Function （支撑函数）
根据凸形的特性2，则可以将方向映射到凸形上的点，而这个奖方向向量映射到形状上的最远的点的函数则叫做支撑函数，则对应的点叫做支撑点。
而这个支撑函数非常有意思的一点是两个凸形support函数相加，既可以得到其Minkowski和的support函数与支撑点。
图2.7 凸形支撑函数、支撑点与Minkowski和的support函数、支撑点间的关系
而面向Minkowski差时，指定第一个凸形A的向量方向，求取其支撑点；接着以该方向的反方向作为第二个凸形B上的方向，求取凸形B上 的支撑点。这两个点相减，就是Minkowski差边界上的支撑点。这对于寻找Minkowski差中包含原点的三角形十分有利。
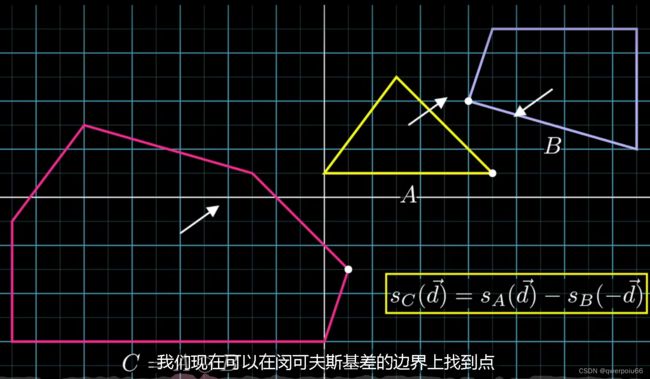图2.8 凸形支撑点与Minkowski差的support支撑点间的关系
有意思的是，通过观察2.7-2.8图，可以发现在求取Minkowski和的支撑点时，凸形A、B上选择的方向是一致的，而在求取Minkowski差的支撑点时，凸形A、B上选择的方向则水平相反。这种差异的来源与Minkowski和\差的定义本身有关。
Support Function 的计算：
Support Function返回的是在凸形边缘制定方向d上最远距离的点v。如图2.9中公式所示，点积可以测量两个向量之间方向相似性，两个向量的方向越相似，则点积的值就越高；而在一个方向上更远的点还会有更高的点积。这一个性质使的求解支撑点成为可能。
图2.9 Support Function 的计算
三、GJK算法及其实施细节
3.1 GJK算法
1. 首先，选取随机方向，并找到该方向上的支撑点，这是simplex的第一个点。
2. 以当前支撑点为向量起点，找到指向原点的向量作为新的方向d，并找到第二个支撑点。
3. 判断第二个支撑点与当前方向d的点积结果是否小于0。通过点积的性质我们可知道，所要两个向量的点积不小于0,两个向量之间的夹角为[0°，90°]。若两个形状要相交，原点与第二个支撑点组成向量与当前方向d的夹角为[0°，90°]，第二个支撑点位置的合理范围如图3.0蓝色区域所示。
1）如果第二个支撑点与方向d的点积小于0，这说明当前的迭代方向上找不到一个能够跨越原 点的支撑点，即第二个支撑点没有落在图3.0的蓝色区域中，两个形状不相交，退出GJK算法。
2） 反之，则将当前第二个支撑点加入到simplex中。
4. 若第二个支撑点合理，则这两个支撑点连成一条直线，垂直于该直线的向量，则为新的方向d并求出新的支撑点，并形成一个三角形。
5. 检查当前三角形是否包含原点。如果包含，则两个形状相交；否则更新方向，添加新的支撑点。选择其距离最接近原点的三角形边的垂直向量并保留这条边上的两个点，删除剩余的一个点，并将该垂直向量作为新的方向d再次寻找第三个支撑点，做下一次迭代与判断。
图3.0 能够跨越原点的第二个支撑点的合理区域（蓝色部位）
3.2 实施细节
问题：
- 如何知道一个Minkowski差上的点是否越过了原点？
- 当我们拥有两个点时，我们怎么选择新的方向？
- 我们如何检测当前形成的三角形是否包含原点？
- 如果当前的三角形不包含原点，我们怎么选择下一个方向
问题1：如何知道一个Minkowski差上的点是否越过了原点？
检查一个点A是否经过原点，其方式如果图3.1所示。从原点将A点视为向量，通过该向量与方向d之间的点积进行判断，当该点积为负数时，则当前点不经过原点；否则，反之。
图3.1 判断当前点经过原点的标准
问题2：当我们拥有两个点时，我们怎么选择新的方向？
首先，当我们有两个点时，A点往往是最新添加的那个点，B点时第一个添加的点。我们首先构建向量AO(O-A)和向量AB（B-A），通过叉乘两个向量，求解出垂直于这两个向量且垂直向上的向量；其次，在求解一个与这个垂直向量和向量AB垂直的向量（三重乘积）。这就是我们说提到的新方向d。
图3.2 基于两个点选择新方向的方法 
图3.3 新方向d的计算方法
问题3与问题4：如何检测当前形成的三角形是否包含原点？如果当前的三角形不包含原点，我们怎么选择下一个方向？
假设我们有三个点A、B、C（其中A往往为最新加入的支撑点）形成一个三角形，我们在三角形的每个边做垂直线以定义空间的区域，形成沃罗诺伊区域；假设B、C两点固定，给定A点所有可能的位置，相应的区域也会改变。为了确定原点最终有可能在哪些区域，我们需要对其进行分析。
图3.4 沃罗诺伊区域
3.1.不可能包含原点的区域及其分析：
Rc：由于支撑点C为第一个支撑点，当我们要选择下一个支撑点时，必然是以C点为起点指向原点的方向作为下一个寻找支撑点的新方向d，这就意味着我们是在与Rc相反的方向向原点搜索，所以原点不可能在Rc中。
Rb：当原点在Rb中，这就意味着B点不能超过原点，因为当前的simplex是无效的，当前选择的B点无效。
Ra：当原点在Ra中，这就意味着A点不能超过原点，因为当前的simplex是无效的,当前选择的A点无效。
图3.5 区域检测及分析
Rbc：BC方向的垂直线用于我们寻找点A，这与Rbc的方向完全相反，因为Rbc不可能包含原点。
3.2. 必须要检查是否包含原点的区域及其分析：
Rab:要是像是A点成为有效点，在给定方向上就要越过原点（即包含原点），那么A点所在的区域如图3.6所所示。在此范围内，Rab有可能包含原点。
图3.6 有效A点所在的区域
为了验证上述猜测，通过三重积定理，定义一个垂直于AB的向量，当当前这个垂直向量与向量A0的点积大于O的时候这就说明原点在Rab中，那么当前的这个simplex则不合适，我们需要重新选择并更新这个simplex，我们将C点从simplex中移除，垂直于AB的向量作为寻找第三个支撑点的新方向d，所以Rab必须要检查。
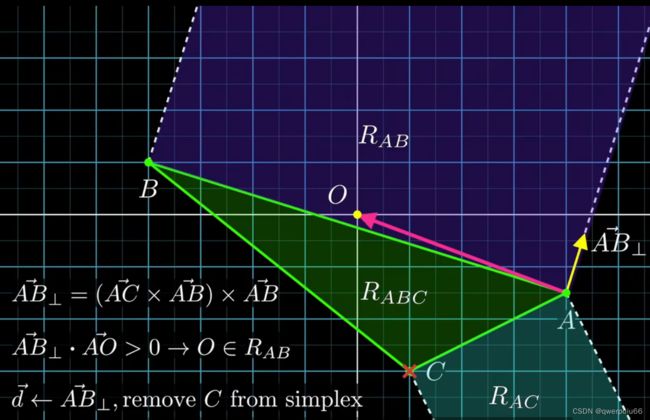图3.7 Rab的检查逻辑
Rac:该区域的检查逻辑与 Rab的检查逻辑类似，当原点在Rac中时，我们就移除当前的B点，重新对点进行选择。
图3.8 Rac的检查逻辑
最重要的一项区域检查：
仅检查区域Rab、Rac两个区域。当Rab、Rac两个区域中都没有包含原点，即垂直于AB、AC的向量与向量AO的点积小于0的时候，这就说明当前原点在其余Rabc中。
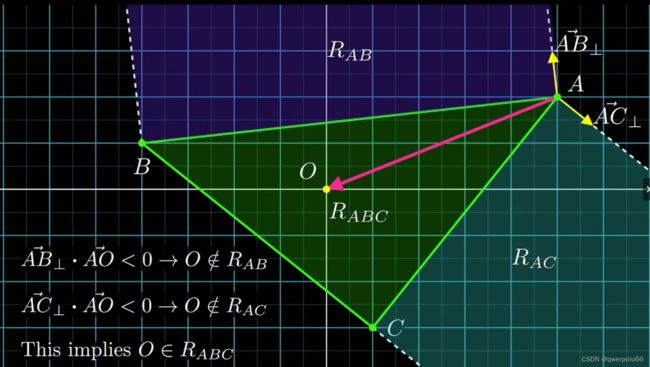图 3.9 原点是否在Rabc中的判别方法
3.3 GJK算法细节
def GJK(s1,s2)
#两个形状s1,s2相交则返回True。所有的向量/点都是三维的，例如（[x,y,0]）
#第一步：选择一个初始方向，这个初始方向可以是随机选择的，但通常来说是两个形状中心之间的向量，即：
d= normalize(s2.center-s1.center)
#第二步：找到支撑点，即第一个支撑点
simplex=[support(s1,s2,d)]
#第三步：找到第一个支撑点后，以第一个支撑点为起点指向原点O的方向为新方向d
d=ORIGIN-simplex[0]
#第四步：开始循环，找下一个支撑点
while True
A=[support(s1,s2,d)]
#当新的支撑点A没有经过原点，那我们就返回False，即两个形状没有相交
if dot(A,d) <0:
return False
#否则，我们就将该点A加入到simplex中
simplex.append(A)
#handleSimplex负责主要逻辑部分。主要负责处理寻找新方向和更新simplex的逻辑内容,当当前simplex包含原点，则返回Ture
if handleSimplex(simplex,d):
return Ture
def handleSimplex(simplex,d)
#如果当前的simplex为直线情况，则进入lineCase(simplex,d)函数,寻找下一个方向d,并返回False，即直线情况下的simplex不包含原点
if len(simplex==2):
return lineCase(simplex,d)
#如果当前的simplex为三角情况，则进入triangleCase(simplex,d,
return triangleCase(simplex,d)
def lineCase(simplex,d)
#构建向量AB与AO,并使用三重积得到下一个方向
B,A = simplex
AB,AO=B-A,ORIGIN-A
ABprep= tripleProd(AB,AO,AB)
d.set(ABprep)
#由于一条直线的情况下，原点不能包含在simplex中，所以返回False
return False
def triangleCase(simplex,d)
#构建向量AB,AC与AO,并来检测原点在空间的哪个区域。
C,B,A = simplex
AB,AC,AO=B-A,C-A,ORIGIN-A
#通过三重积分别得到垂直于AB、AC的向量，检测区域Rab、Rac中是否包含原点。
ABprep= tripleProd(AC,AB,AB)
ACprep= tripleProd(AB,AC,AC)
#如果原点在AB区域中，我们移除点C以寻找更加完美的simplex，新的方向就是垂直于AB的向量
if dot(ABprep,AO)>0:
simplex.remove(C);d.set(ABprep)
return False
#如果原点在AC区域中，我们移除点B以寻找更加完美的simplex，新的方向就是垂直于AC的向量
elif dot(ACprep,AO)>0:
simplex.remove(Ba);d.set(ACprep)
return False
#如果这两种情况都不符合，那就说明当前的三角形中包含原点，两个形状相交
return Ture
def support(s1,s2,d)
#取第一个形状上方向d上最远点并减去第二个形状上相反反向（-d）上最远的点
return s1.furthestPoint(d)-s2.furthestPoint(-d)仅为加强自己的理解与记忆，如若涉及到侵权问题，请联系我我就删除哟~