【LeetCode周赛】2022上半年题目精选集——数学
文章目录
- 2183. 统计可以被 K 整除的下标对数目⭐⭐⭐⭐⭐
-
- 思路——数论(一个数乘上另一个数x是k的倍数,x最小是多少?)
-
- 代码1——统计每个数的因子
- 代码2——统计k的因子
- 2245. 转角路径的乘积中最多能有几个尾随零
-
- 思路(因子2和5的个数 + 前缀和)⭐⭐⭐⭐⭐
- 代码
- 2281. 巫师的总力量和⭐⭐⭐⭐⭐
-
- 思路——贡献法(单调栈求左右端点) + 前缀和的前缀和
- 代码
- 2310. 个位数字为 K 的整数之和
-
- 解法——枚举集合的大小
-
- 代码1——自己写的
- 代码2——力扣官解
https://leetcode.cn/circle/discuss/G0n5iY/
2183. 统计可以被 K 整除的下标对数目⭐⭐⭐⭐⭐
1 <= nums.length <= 10^5
1 <= nums[i], k <= 10^5
思路——数论(一个数乘上另一个数x是k的倍数,x最小是多少?)
对于一个固定的数字 nums[j] ,要想和 nums[i] 配对,那么 nums[i] 必须是某个数字 x 的倍数。
那么 x 最小是多少呢? (为了找到所有符合条件的 nums[i] ,我们需要找到最小的 x)
从数论的结论来看, x = k g c d ( n u m s [ j ] , k ) x = \frac{k}{gcd(nums[j], k)} x=gcd(nums[j],k)k,这里 k 就是题目中的 k。
为什么呢?可以从因子的角度去考虑,如果 nums[j] 和 k 有一些公因子,那么可以从 k 中除去这些公因子,这样 x 会变小,那么除去最大公因子是最优的。
代码1——统计每个数的因子
我们可以不断枚举 nums[j],在这个过程中记录前面枚举过的 x 的倍数有多少个记为 cnt[x],那么枚举到 nums[j] 的时候就给答案加上多少。
class Solution {
final static int mx = 100001;
// 记录每个数字的所有因子
static List<List<Integer>> divisors = new ArrayList(mx);
static {
for (int i = 0; i < mx; ++i) divisors.add(new ArrayList());
for (int i = 1; i < mx; ++i) {
for (int j = i; j < mx; j += i) {
// j是i的倍数,所以把i放进j的因子列表里
divisors.get(j).add(i);
}
}
}
public long countPairs(int[] nums, int k) {
long ans = 0;
Map<Integer, Integer> cnt = new HashMap();
for (int num: nums) {
ans += cnt.getOrDefault(k / gcd(num, k), 0);
for (int d: divisors.get(num)) {
cnt.merge(d, 1, Integer::sum);
}
}
return ans;
}
public static int gcd(int a, int b) {
return b == 0? a: gcd(b, a % b);
}
}
代码2——统计k的因子
注意到 x 是 k 的因子,因此可以将代码 1 中统计 num 的因子改为 统计 num 是 k 的哪些因子的倍数,这可以通过 枚举 k 的所有因子 来判断。
class Solution {
public long countPairs(int[] nums, int k) {
// 统计k的因子
List<Integer> divisors = new ArrayList();
for (int d = 1; d * d <= k; ++d) {
if (k % d == 0) {
divisors.add(d);
if (d * d < k) divisors.add(k / d);
}
}
long ans = 0;
Map<Integer, Integer> cnt = new HashMap();
for (int num: nums) {
ans += cnt.getOrDefault(k / gcd(num, k), 0);
for (int d: divisors) {
if (num % d == 0) cnt.merge(d, 1, Integer::sum);
}
}
return ans;
}
public static int gcd(int a, int b) {
return b == 0? a: gcd(b, a % b);
}
}
2245. 转角路径的乘积中最多能有几个尾随零
2245. 转角路径的乘积中最多能有几个尾随零
m == grid.length
n == grid[i].length
1 <= m, n <= 10^5
1 <= m * n <= 10^5
1 <= grid[i][j] <= 1000
思路(因子2和5的个数 + 前缀和)⭐⭐⭐⭐⭐
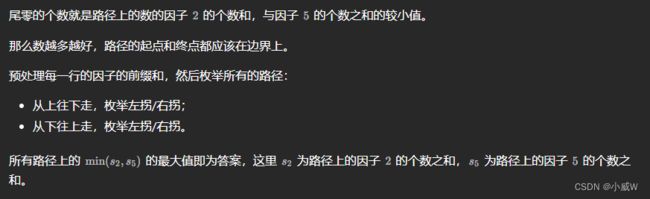
计算出每个数字含有多少个 2 和 多少个 5,最后尾随 0 的个数就是 2 和 5 的数量的最小值。
代码
class Solution {
static int[][] c25 = new int[1001][2];
static {
// 预处理,递推出每个数的因子2和因子5的个数
for (int i = 2; i <= 1000; ++i) {
if (i % 2 == 0) c25[i][0] = c25[i / 2][0] + 1;
if (i % 5 == 0) c25[i][1] = c25[i / 5][1] + 1;
}
}
public int maxTrailingZeros(int[][] grid) {
int m = grid.length, n = grid[0].length, ans = 0;
int[][][] s = new int[m][n + 1][2];
for (int i = 0; i < m; ++i) {
for (int j = 0; j < n; ++j) {
// 每行的因子2或5的前缀和数量
s[i][j + 1][0] = s[i][j][0] + c25[grid[i][j]][0];
s[i][j + 1][1] = s[i][j][1] + c25[grid[i][j]][1];
}
}
for (int j = 0; j < n; ++j) { // 枚举每一列
// 从上往下,枚举左拐还是右拐
for (int i = 0, s2 = 0, s5 = 0; i < m; ++i) {
s2 += c25[grid[i][j]][0];
s5 += c25[grid[i][j]][1];
int left = Math.min(s2 + s[i][j][0], s5 + s[i][j][1]);
int right = Math.min(s2 + s[i][n][0] - s[i][j + 1][0], s5 + s[i][n][1] - s[i][j + 1][1]);
ans = Math.max(ans, Math.max(left, right));
}
// 从下往上,枚举左拐还是右拐
for (int i = m - 1, s2 = 0, s5 = 0; i >= 0; --i) {
s2 += c25[grid[i][j]][0];
s5 += c25[grid[i][j]][1];
int left = Math.min(s2 + s[i][j][0], s5 + s[i][j][1]);
int right = Math.min(s2 + s[i][n][0] - s[i][j + 1][0], s5 + s[i][n][1] - s[i][j + 1][1]);
ans = Math.max(ans, Math.max(left, right));
}
}
return ans;
}
}
注意学习 递推出每个数的因子2和因子5的个数 的方法。
即:
static int[][] c25 = new int[1001][2];
static {
// 预处理,递推出每个数的因子2和因子5的个数
for (int i = 2; i <= 1000; ++i) {
if (i % 2 == 0) c25[i][0] = c25[i / 2][0] + 1;
if (i % 5 == 0) c25[i][1] = c25[i / 5][1] + 1;
}
}
2281. 巫师的总力量和⭐⭐⭐⭐⭐
1 <= strength.length <= 105
1 <= strength[i] <= 109
思路——贡献法(单调栈求左右端点) + 前缀和的前缀和
笔者认为本题的主要难点在于 前缀和的前缀和求法。
关于贡献法可见:【算法】贡献法相关题目练习
关于前缀和的前缀和的计算可见:https://leetcode.cn/problems/sum-of-total-strength-of-wizards/solutions/1510399/dan-diao-zhan-qian-zhui-he-de-qian-zhui-d9nki/ 或 下图计算过程。

注意这里说的所有子数组指的是所有包括元素 strength[i] 的子数组。
代码
class Solution {
public int totalStrength(int[] strength) {
final int mod = (int)1e9 + 7;
int n = strength.length;
int[] s = new int[n + 1], ss = new int[n + 2];
// 前缀和的前缀和
for (int i = 0; i < n; ++i) {
s[i + 1] = (s[i] + strength[i]) % mod;
ss[i + 2] = (ss[i + 1] + s[i + 1]) % mod;
}
int[] left = new int[n], right = new int[n];
Arrays.fill(left, -1);
Arrays.fill(right, n);
Deque<Integer> stk = new ArrayDeque();
for (int i = 0; i < n; ++i) {
while (!stk.isEmpty() && strength[i] <= strength[stk.peek()]) right[stk.pop()] = i;
if (!stk.isEmpty()) left[i] = stk.peek();
stk.push(i);
}
long ans = 0;
for (int i = 0; i < n; ++i) {
int l = left[i] + 1, r = right[i] - 1;
// 前缀和的前缀和推出的公式
long tot = ((long)(i - l + 1) * (ss[r + 2] - ss[i + 1]) - (long)(r - i + 1) * (ss[i + 1] - ss[l])) % mod;
ans = (ans + tot * strength[i]) % mod;
}
return (int)(ans + mod) % mod;
}
}
2310. 个位数字为 K 的整数之和
2310. 个位数字为 K 的整数之和

提示:
0 <= num <= 3000
0 <= k <= 9
解法——枚举集合的大小
我们可以知道集合的大小不会超过 10,因为 11 个 个位是 k 的数字相乘,最后的个位数字还是 k ,没有影响。
代码1——自己写的
class Solution {
public int minimumNumbers(int num, int k) {
if (num == 0) return 0;
int n = num % 10, ans = 1;
while (ans < 11 && (ans * k % 10 != n)) ++ans;
return ans <= 10 && ans * k <= num? ans: -1;
}
}
自己写的代码丑陋了一下,因为循环写的不好所以需要对结果加一些额外的判断。
代码2——力扣官解
class Solution {
public int minimumNumbers(int num, int k) {
if (num == 0) return 0;
for (int i = 1; i <= 10; ++i) {
if (k * i <= num && (num - k * i) % 10 == 0) return i;
}
return -1;
}
}
官解的答案优雅很多,依次判断 1 ~ 10 是否满足答案,满足就返回,不满足就最后返回 -1。


