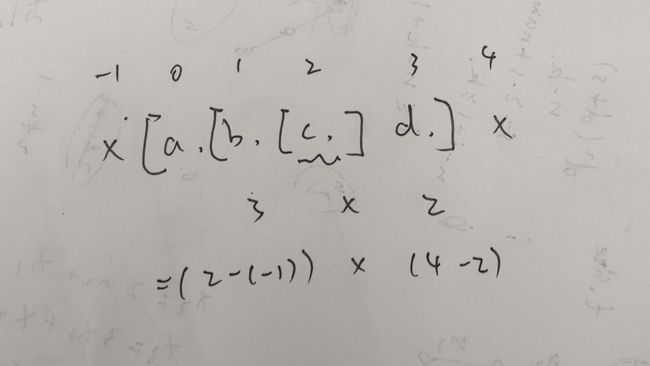【算法】贡献法相关题目练习
文章目录
- 贡献法介绍
- 前置知识:单调栈
-
- 例题——496. 下一个更大元素 I
- 贡献法相关题目
-
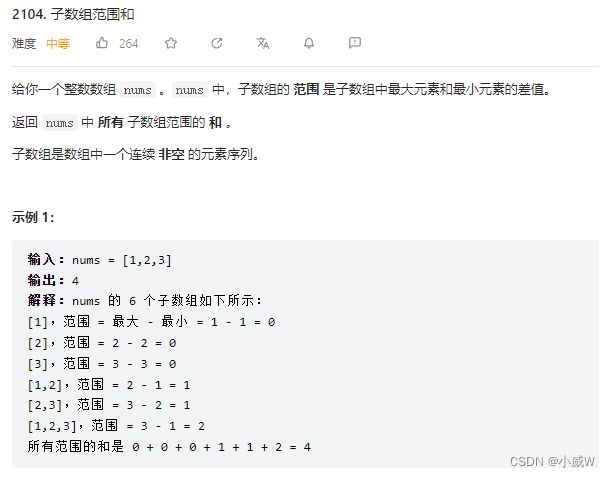
- 2104. 子数组范围和
-
- 思路
- 代码1——自己写的代码
- 代码2——最小值的贡献和最大值的贡献的关系
- 907. 子数组的最小值之和
-
- 代码1——单调栈+计算贡献
- 代码2——寻找左右最小值的同时计算答案
- 1856. 子数组最小乘积的最大值
- 2681. 英雄的力量
- 2281. 巫师的总力量和
- 相关链接
本文介绍一些 使用 贡献法 的算法题目。
贡献法介绍
就是计算每个元素对最终答案的贡献是多少,在枚举的过程中加起来。(在枚举之前通常会使用单调栈找到左右第一个比当前元素更大或更小的元素所在的位置)
所以这类题目的关键是想到如何在枚举的过程中计算各个元素的贡献。
前置知识:单调栈
所谓单调栈就是栈里面的数字是单调递增或单调递减的,可以用来确定某个数字前一个或后一个更小或更大的数字。
例题——496. 下一个更大元素 I
496. 下一个更大元素 I

nums1 中每个元素都会在 nums2 中出现,
只需要枚举 nums2 ,在枚举的过程中使用单调栈找到第一个更大的元素,使用哈希表记录下来。
class Solution {
public int[] nextGreaterElement(int[] nums1, int[] nums2) {
int[] ans = new int[nums1.length];
Deque<Integer> stk = new ArrayDeque(); // 递减的单调队列
Map<Integer, Integer> m = new HashMap(); // 存放每个数字下一个更大的数字
for (int i = 0; i < nums2.length; ++i) {
while (!stk.isEmpty() && nums2[i] > stk.peek()) {
// 一个数被弹出来的时候,说明它遇到了第一个比它大的元素
m.put(stk.pop(), nums2[i]);
}
stk.push(nums2[i]);
}
for (int i = 0; i < nums1.length; ++i) {
ans[i] = m.getOrDefault(nums1[i], -1);
}
return ans;
}
}
贡献法相关题目
2104. 子数组范围和
思路
分别计算出每个元素作为最大值的子数组数量和作为最小值的子数组数量,那么这个元素对最终答案的贡献就是 x * (a - b) ,其中 x = nums[i],a 和 b 分别是最大值的子数组数量和作为最小值的子数组数量。(因为题目求的是子数组中最大元素和最小元素的差值,所以作为最大元素时前面是加号,作为最小元素时前面是减号。
Q:如何求当前元素作为最大值时的子数组数量?
A:找到当前元素左右两边第一个大于当前元素的元素位置,假设当前元素下标为 i ,左右两边第一个大于当前元素的下标分别为 x 和 y ,那么子数组的数量就是 (i - x) * (y - i)。(看不懂就看下图)
代码1——自己写的代码
使用两个单调栈,分别求出每个数字左右两侧第一个大于或小于该元素的值。
为了避免重复计算,可以看出每个数字找到的一侧为严格大于或小于,另一侧为大于等于或小于等于。
class Solution {
public long subArrayRanges(int[] nums) {
int n = nums.length;
// 分别计算每个数字作为最大元素的贡献和最小元素的贡献,最大元素贡献之和减去最小元素贡献之和即为最终答案
//
Deque<Integer> stk1 = new ArrayDeque(), stk2 = new ArrayDeque();
int[] rightLarge = new int[n + 1], leftLarge = new int[n + 1];
int[] rightSmall = new int[n + 1], leftSmall = new int[n + 1];
// 初始左右两边为 -1 和 n。
Arrays.fill(rightLarge, n);
Arrays.fill(rightSmall, n);
Arrays.fill(leftLarge, -1);
Arrays.fill(leftSmall, -1);
for (int i = 0; i < n; ++i) {
while (!stk1.isEmpty() && nums[i] >= nums[stk1.peek()]) {
int x = stk1.pop();
rightLarge[x] = i; // 右侧大于等于
}
if (!stk1.isEmpty()) leftLarge[i] = stk1.peek(); // 左侧严格大于
stk1.push(i);
while (!stk2.isEmpty() && nums[i] <= nums[stk2.peek()]) {
int x = stk2.pop();
rightSmall[x] = i; // 右侧小于等于
}
if (!stk2.isEmpty()) leftSmall[i] = stk2.peek(); // 左侧严格小于
stk2.push(i);
}
long ans = 0;
for (int i = 0; i < n; ++i) {
// 给答案加入贡献
ans += (long)nums[i] * ((rightLarge[i] - i) * (i - leftLarge[i]) - (rightSmall[i] - i) * (i - leftSmall[i]));
}
return ans;
}
}
代码2——最小值的贡献和最大值的贡献的关系
我们只需要计算最大值的贡献,然后将所有元素取反,再算一遍就是最小值的贡献,两次计算结果求和即为最终答案。
class Solution {
public long subArrayRanges(int[] nums) {
long ans = solve(nums);
Arrays.setAll(nums, i -> -nums[i]); // 将所有元素取反
return ans + solve(nums);
}
public long solve(int[] nums) {
int n = nums.length;
Deque<Integer> stk = new ArrayDeque();
int[] right = new int[n], left = new int[n];
Arrays.fill(right, n);
Arrays.fill(left, -1);
for (int i = 0; i < n; ++i) {
while (!stk.isEmpty() && nums[i] >= nums[stk.peek()]) {
right[stk.pop()] = i; // 右侧第一个大于等于的
}
if (!stk.isEmpty()) left[i] = stk.peek(); // 左侧第一个严格大于的
stk.push(i);
}
long ans = 0;
for (int i = 0; i < n; ++i) {
ans += (long)nums[i] * (right[i] - i) * (i - left[i]);
}
return ans;
}
}
Q:为什么所有元素取反后算的就是最小值的贡献?
A:举例 1 2 3,取反后成为 -1 -2 -3,正好原本想找的最小值变成了最大值(它会被找到),同时前面的符号也发生了变化(它会被正确计算)。
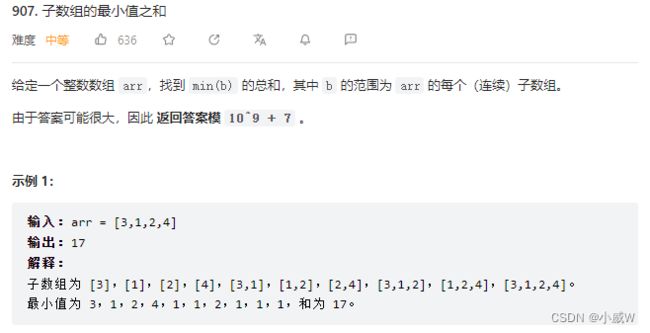
907. 子数组的最小值之和
907. 子数组的最小值之和
这道题目是比 2104. 子数组范围和 要简单的,只需要计算每个元素作为最小值时的贡献就好了。
代码1——单调栈+计算贡献
class Solution {
private static final int MOD = (int)1e9 + 7;
public int sumSubarrayMins(int[] arr) {
long ans = 0; // 使用long总归是有利于避免溢出
int n = arr.length;
// 计算每个数字作为最小值的贡献,即找到左右两侧第一个小于它的(一边严格小于,另一边小于等于)
Deque<Integer> stk = new ArrayDeque();
int[] right = new int[n], left = new int[n];
Arrays.fill(left, -1);
Arrays.fill(right, n);
for (int i = 0; i < n; ++i) {
while (!stk.isEmpty() && arr[i] <= arr[stk.peek()]) {
right[stk.pop()] = i;
}
if (!stk.isEmpty()) left[i] = stk.peek();
stk.push(i);
}
for (int i = 0; i < n; ++i) {
ans = (ans + (long)arr[i] * (right[i] - i) * (i - left[i])) % MOD;
}
return (int)ans;
}
}
代码2——寻找左右最小值的同时计算答案
进一步地,由于栈顶下面的元素正好也是栈顶的左边界,所以甚至连 left 和 right 数组都可以不要,直接在出栈的时候计算贡献。
class Solution {
private static final int MOD = (int)1e9 + 7;
public int sumSubarrayMins(int[] arr) {
long ans = 0; // 使用long总归是有利于避免溢出
int n = arr.length;
// 计算每个数字作为最小值的贡献,即找到左右两侧第一个小于它的(一边严格小于,另一边小于等于)
Deque<Integer> stk = new ArrayDeque();
stk.push(-1); // 哨兵,左端点至少为-1(也就是左边没有比它小的)这里的-1是下标
for (int i = 0; i <= n; ++i) {
int x = i < n? arr[i]: -1; // 加入这个-1让栈里所有元素最后都能出来(这里的-1是值)
while (stk.size() > 1 && x <= arr[stk.peek()]) {
int id = stk.pop();
ans = (ans + (long)arr[id] * (id - stk.peek()) * (i - id)) % MOD;
}
stk.push(i);
}
return (int)ans;
}
}
每个元素的贡献是在它出栈是计算的。
需要将 i 遍历到 n,这样才能让下标在 n - 1 的元素出栈计算贡献。
栈底首先加了一个 -1,这是作为左边界的。(即当前元素左边没有比它小的元素时,那么它的子数组左边界下标为 -1。这跟Arrays.fill(left, -1)是一个道理。)
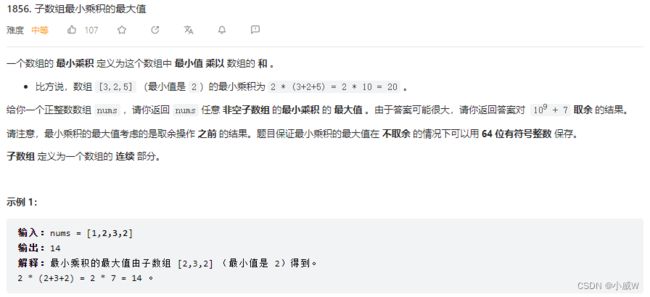
1856. 子数组最小乘积的最大值
1 <= nums.length <= 10^5
1 <= nums[i] <= 10^7
- 这道题要求最大值。
- 这道题需要求子数组的和,所以可以使用前缀和提前处理。
- 这道题是找最小值的贡献,所以使用单调栈找到左右两边的最小值的下标。
- 数组中所有元素都是大于0的,因此得到最大结果那个非空子数组一定越长越好,我们只需要得到当前元素作为最小值时的最长子数组即可。
class Solution {
private static final long MOD = (long)1e9 + 7;
// 找左右两边第一个更小值的下标+前缀和
public int maxSumMinProduct(int[] nums) {
int n = nums.length;
long ans = 0;
long[] s = new long[n + 1];
for (int i = 0; i < n; ++i) s[i + 1] = s[i] + nums[i]; // 计算前缀和
Deque<Integer> stk = new ArrayDeque();
stk.push(-1);
for (int i = 0; i <= n; ++i) {
int cur = i == n? 0: nums[i];
while (stk.size() > 1 && cur <= nums[stk.peek()]) {
int x = stk.pop();
ans = Math.max(ans, nums[x] * (s[i] - s[stk.peek() + 1])); // 更新答案
}
stk.push(i);
}
return (int)(ans % MOD);
}
}
同上一题的代码二一样,每个元素是在出栈时被计算对答案的贡献的。
2681. 英雄的力量
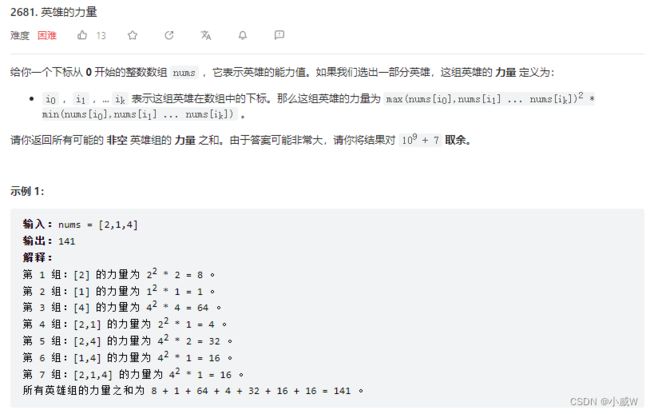
提示:
1 <= nums.length <= 10^5
1 <= nums[i] <= 10^9
根据数据范围,这道题目必须使用 O ( n ) O(n) O(n) 时间复杂度的算法。
由于是任选一部分英雄,因此数据的顺序不影响最后的结果,所以可以先排序。
从前向后进行枚举,每次枚举到一个数字,计算其作为最大值的贡献。
下面举一个例子:(重要!思考的过程)
考虑 a, b, c, d, e 五个数字,当前枚举到了 d。
此时 a, b, c 分别作为最小值的贡献为: a ∗ 2 2 + b ∗ 2 1 + c ∗ 2 0 a*2^2 + b*2^1 + c*2^0 a∗22+b∗21+c∗20,记为 s s s。(因为选a的时候b和c都是可选可不选,选b的时候c可选可不选,选c的时候a和b都不能选)
那么此时对答案的贡献为: d 3 + d 2 ∗ s = d 2 ∗ ( d + s ) d^3+d^2*s = d^2*(d+s) d3+d2∗s=d2∗(d+s)
继续枚举到 e e e,
此时 a, b, c, d 分别作为最小值的贡献为: a ∗ 2 3 + b ∗ 2 2 + c ∗ 2 1 + d ∗ 2 0 = 2 ∗ ( a ∗ 2 2 + b ∗ 2 1 + c ∗ 2 0 ) + d ∗ 2 0 = 2 ∗ s + d a*2^3 + b*2^2 + c*2^1 + d*2^0 = 2*(a*2^2 + b*2^1 + c*2^0) + d*2^0 = 2 *s + d a∗23+b∗22+c∗21+d∗20=2∗(a∗22+b∗21+c∗20)+d∗20=2∗s+d
得到了新的 s = 2 ∗ s + n u m s [ i ] s = 2 * s + nums[i] s=2∗s+nums[i]
此时我们就得到了两个重要的递推式:
a n s + = n u m s [ i ] ∗ n u m s [ i ] ∗ ( n u m s [ i ] + s ) ans += nums[i] * nums[i] * (nums[i] + s) ans+=nums[i]∗nums[i]∗(nums[i]+s)
s = 2 ∗ s + n u m s [ i ] s = 2 * s + nums[i] s=2∗s+nums[i]
class Solution {
private static final long MOD = (int)1e9 + 7;
public int sumOfPower(int[] nums) {
long ans = 0, sum = 0;
// 元素的顺序不影响答案,所以先排序
Arrays.sort(nums);
// 枚举每个英雄,计算其作为最大值时的力量贡献
for (long x: nums) {
ans = (ans + x * x % MOD * (x + sum)) % MOD; // 更新答案
sum = (sum * 2 + x) % MOD; // 更新 s
}
return (int)ans;
}
}
本题的关键就在于想到 先排序。
以及 计算贡献时使用递推式。
2281. 巫师的总力量和
这道题属于特别特别难的题目,如果这道题可以自己做出来,那这种类型的题目就算是出师了!
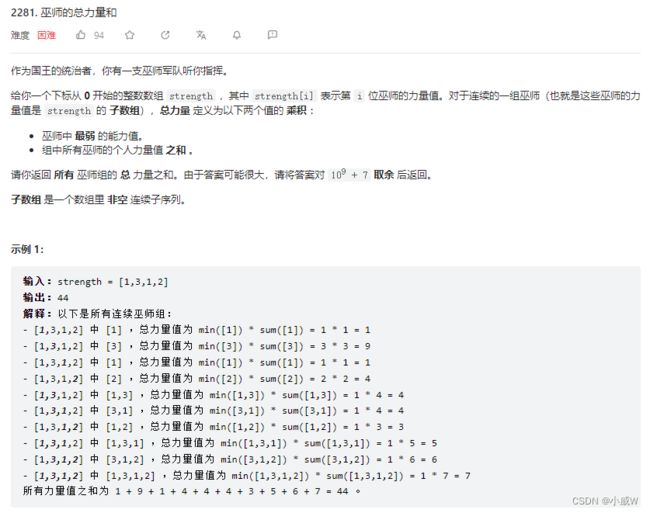
提示:
1 <= strength.length <= 10^5
1 <= strength[i] <= 10^9
这道题的一个关键难点在于,枚举每个巫师作为最弱巫师时,需要计算出它作为最弱巫师的所有子数组的和的总和,而不仅仅是找到它作为最弱巫师时的左右两个边界。
一个子数组的和可以通过前缀和快速计算,就像 1856. 子数组最小乘积的最大值 中使用的那样。
那么如何计算子数组的元素和的和?

笔者认为这个前缀和的前缀和才是这道题目最难的部分。
class Solution {
private static final long MOD = (long)1e9 + 7;
public int totalStrength(int[] strength) {
int n = strength.length;
// 我们需要前缀和的前缀和,即范围内所有子数组的和的和
long s = 0;
long[] ss = new long[n + 2];
for (int i = 1; i <= n; ++i) {
s += strength[i - 1];
ss[i + 1] = (ss[i] + s) % MOD;
}
int[] left = new int[n], right = new int[n];
Arrays.fill(left, -1);
Arrays.fill(right, n);
Deque<Integer> stk = new ArrayDeque();
for (int i = 0; i < n; ++i) {
while (!stk.isEmpty() && strength[i] <= strength[stk.peek()]) {
right[stk.pop()] = i;
}
if (!stk.isEmpty()) left[i] = stk.peek();
stk.push(i);
}
long ans = 0;
for (int i = 0; i < n; ++i) {
int l = left[i] + 1, r = right[i] - 1; // [l, r] 左闭右开
// 最好先把计算公式写下来再翻译成代码
long tot = ((i - l + 1) * (ss[r + 2] - ss[i + 1]) - (r - i + 1) * (ss[i + 1] - ss[l])) % MOD;
ans = (ans + strength[i] * tot) % MOD;
}
return (int)((ans + MOD) % MOD);
}
}
参考资料:https://leetcode.cn/problems/sum-of-total-strength-of-wizards/solution/dan-diao-zhan-qian-zhui-he-de-qian-zhui-d9nki/
相关链接
【力扣周赛】第 352 场周赛 这场周赛最后一题可以使用贡献法。