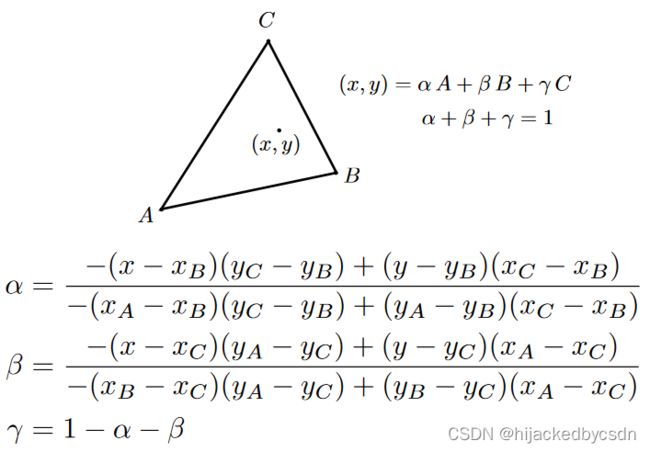GAMES101 学习笔记 Lecture 7~9
目录
- GAMES101 学习笔记 Lecture 7~
-
- 往期作业汇总帖
- Lecture 7: Shading 1 (Illumination, Shading and Graphics Pipeline)
-
- 画家算法
- 画家算法的排序问题
- Z-Buffer
- Shading 的定义
- Blinn-Phong 反射光模型
-
- 光的分类
- 模型参数
- 着色是局部的
- 漫反射
- 点光源的能量
- 漫反射公式
- 漫反射公式是不是要加能量的修正项
- 作业 2
-
- 文件删除之后的错误
- 背景了解
- C++17 结构化绑定
- insideTriangle
- get_index
- 三角形遮挡顺序
- SSAA
- SSAA 不出现黑边的正确写法
- Lecture 8 Shading 2
-
- Blinn-Phong 反射光模型 续
-
- 漫反射项
- 高光项
- 高光项夹角近似之后得到的夹角与原来的夹角之间的关系
- 高光计算公式相关的能量损失
- Phong 与 Blinn-Phong
- 环境光
- 能量?离得远觉得暗?人眼到物体的距离为什么不考虑?
- 着色频率
- Blinn-Phong 模型 != Phong Shading
- 怎么计算顶点的法线
- 怎么计算逐像素的法线
- 图形管线
- 纹理映射
- Lecture 9: Shading 3 (Texture Mapping cont)
-
- 插值
- 重心坐标
-
- 重心坐标的计算
- 重心坐标在投影操作之后会变化
- 纹理采样
-
- 高分辨率的物体,去采样低分辨率的纹理
- 双线性插值
- 低分辨率的物体,去采样高分辨率的纹理
- 纹理的采样范围大小
- 范围查询的方式 Mipmap
- 怎么知道片元中一个像素对应纹理上的多大的采样点
- 不同 level 的 Mipmap 之间的插值:三线性插值
- 各向异性过滤
- EWA 过滤
- 作业 3
-
- 在计算齐次坐标的归一化时保留深度
- 重心坐标
-
- 自己写的重心坐标计算
- 原来的重心坐标在计算的时候可能计算出超出 [0, 1] 的 UV
- 自己写的 computeBarycentric2D 跟原版的不一样
- 出现负的重心坐标是合理的,因为点可能位于三角形边上
- 透视矫正的公式推导与对应代码写法
- 第一个任务 rasterize_triangle;实现 normal shader
-
- cmake 查找不到 opencv
- make : 无法将“make”项识别为 cmdlet、函数、脚本文件或可运行程序的名称
- make: *** No targets specified and no makefile found. Stop.
- can't open/read file: check file path/integrity
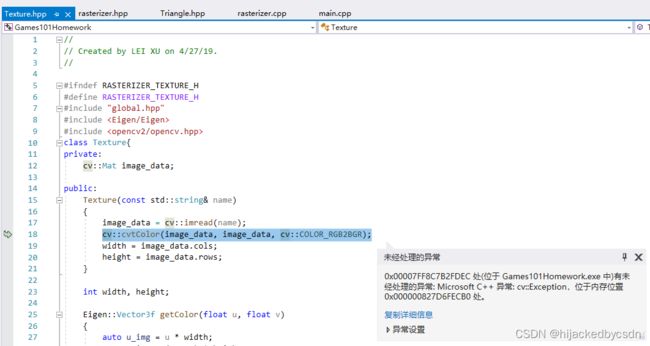
- cv::cvtColor(image_data, image_data, cv::COLOR_RGB2BGR); 报错
- 编译出来的 exe 点击执行没有弹出 opencv 窗口
- 实现 phong_fragment_shader
-
- shader 中的光源
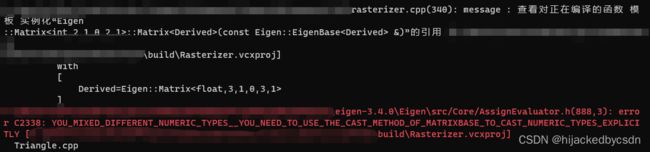
- 报错 C2338 INVALID_VECTOR_VECTOR_PRODUCT__IF_YOU_WANTED_A_DOT_OR_COEFF_WISE_PRODUCT_YOU_MUST_USE_THE_EXPLICIT_FUNCTIONS
- 做出来黑白的效果
- 整个模型变成灰色:着色点的坐标空间搞错了
- 正常的 phong 效果图?
- 透视校正重心坐标;法线乘以 MV 逆变换
- 环境光只计算一次
- 实现 texture_fragment_shader
-
- 模型显示出蓝紫色的混乱的颜色
- libpng warning:iCCP:known incorrect sRGB profile
- Bump mapping
- displacement mapping
-
- 高光位置不一样:可能是 interpolated_shadingcoords 忘算了
- 调试方法
- 更换模型
-
- Crate 渲染错误
- 双线性插值
GAMES101 学习笔记 Lecture 7~
往期作业汇总帖
https://games-cn.org/forums/topic/allhw/
Lecture 7: Shading 1 (Illumination, Shading and Graphics Pipeline)
画家算法
先画后面的,再画前面的
画家算法的排序问题
但是画家算法没有规定在 z 相同的时候该怎么画
假设是左下右上的画法:
但是如果是右上左下的顺序,就是不对的
也就是说覆盖关系出错了
这里就引出了一个问题,如果单看某一个面的 z 值(比如说用这个面的形心的 z 值来代表这个面的 z 值),那么就会引出排序问 题
同理,另外一个可能产生排序问题的例子:
Z-Buffer
对面不好排,而对像素好排
Z-Buffer 算法就是计算像素的深度,然后每个像素点的颜色取深度最小的那个点的颜色
伪代码:
for(each triangle T)
for(each sample (x,y,z) in T)
if(z < zbuffer[x,y]) // closest sample so far
framebuffer[x,y] = rgb; // update color
zbuffer[x,y] = z; // update depth
else
; // do nothing, this sample is occluded
Z-Buffer 看上去好像解决了三角形图元排序的问题
但是实际上他不是对三角形图元的排序。先不说三角形图元的排序也可能存在若干个图元成环且相互遮挡的死结,只说 Z-Buffer 的本质是记录像素的 z 值的最小值,而不是对三角形图元的排序
所以 Z-Buffer 是 o(n) 时间,低于排序的最低的 o(nlogn),是合理的
Z-Buffer 是与三角形图元之间的顺序无关的
Z-Buffer 假设没有两个像素的深度是相同的,如果存在像素深度相同就很麻烦,因为浮点数之间的相等比较是很难的
Z-Buffer 处理不了透明物体的深度,透明物体需要特殊处理
Shading 的定义
对不同物体应用不同材质
Blinn-Phong 反射光模型
光的分类
specular light 镜面光 光源 -> 物体镜面反射的光
diffuse light 漫射光 光源 -> 物体漫反射的光
ambient light 环境光 光源 -> 环境物体 -> 环境物体反射的光打到目标物体上 -> 目标物体反射的来自环境物体的光
如果要计算真实的环境光,那么对于每一个物体,都要考虑周围所有物体,很复杂,所以为了简单,可以设环境光为常量
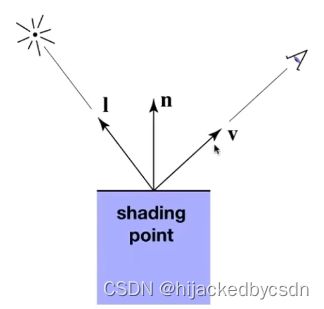
模型参数
-
观测方向 v
-
物体表面法线方向 n
-
光源方向 l
-
物体表面参数(颜色,光泽度 shininess)
表示方向都是单位向量
着色是局部的

着色是局部的,也就是说他只考虑光线一定会过来到这个自己的这个点上,他不考虑这个全局中,物体其他点,其他部分对光线的影响,比如是否遮挡

这个物体的某一点的颜色的计算没有考虑光线会被本物体本身的其他部分遮挡
地面等其他物体也不会考虑光线被其他物体阻挡
所以着色是局部的,与阴影无关
漫反射
同样的光,但是物体以不同角度接收到不同量的光线
但是物体 60 度倾斜,就只能接收到三条光线
因此可以用 cos 来判断接收到的光线的大小
同时,既然要讨论接收到的光线(能量),就要考虑单位面积,才有对比考虑的意义
点光源的能量
现在我们已经知道了,面的法向怎么影响面接收到的能量
但是要具体算出能量的数值,我们还需要知道来源的能量的数值的大小
我们可以看一个点光源
假设点光源每时每刻都在向外发出光,同一个时间发出的光到达的位置是一个球形
也就是说,同一个时间发出的能量分布在一个球壳上
假设光在传播过程中没有能量损失,也就是每一个球壳上的光的能量应该是相等的
那么球壳越大,球壳上单位面积的能量越小
又因为球的面积公式是 S = 4 π r 2 S = 4\pi r^2 S=4πr2
所以取两个球壳 S1 S2,令这两个球壳上的单位面积的能量为 I1 I2,那么有
I 1 S 1 = I 2 S 2 I_1 S_1 = I_2 S_2 I1S1=I2S2
=> I 1 4 π r 1 2 = I 2 4 π r 2 2 I_1 4\pi r_1^2 = I_2 4\pi r_2^2 I14πr12=I24πr22
=> I 1 r 1 2 = I 2 r 2 2 I_1 r_1^2 = I_2 r_2^2 I1r12=I2r22
可以发现它们之间是平方反比的关系
如果我定义 r1 = 1,I1 = I
那么我就有 I 2 = I / r 2 2 I_2 = I/r_2^2 I2=I/r22
漫反射公式
那么这里我就得到了漫反射的公式:
L d = k d I r 2 max ( 0 , n ⋅ l ) L_d = k_d \dfrac{I}{r^2}\max{(0, \mathbf{n} \cdot \mathbf{l})} Ld=kdr2Imax(0,n⋅l)
其中 k d k_d kd 是漫反射系数,物理意义与颜色相关, L d L_d Ld 表示漫反射光强, n \mathbf{n} n 表示着色点法向, l \mathbf{l} l 表示光源方向
和 0 取 max 的意思是,光线从物体背面过来的话,认为没有物理意义,漫反射没有贡献,所以光强是 0
k d k_d kd 也可以表示他吸收了多少光强,反射出去多少光强
如果 k d = 1 k_d = 1 kd=1 表示完全不吸收光线, k d = 0 k_d = 0 kd=0 表示完全吸收光线
假设 k d k_d kd 是一个长度为 3 的向量,三个值对应在 rgb 通道上对颜色的反射率,那么 L d L_d Ld 就可以返回一个颜色
因为是漫反射,所以观测者从哪里看,看到的光强是一样的,所以公式中与 v \mathbf{v} v 无关
这并不意味这物体整体一个亮度,而是说从不同方向看物体上的同一点的亮度是相同的
漫反射公式是不是要加能量的修正项
可以加,Blinn-Phong 反射光模型只是一个经验模型
作业 2
文件删除之后的错误
如果是在一个项目里做多个作业,运行新作业的 main.cpp 的时候可能会提示找不到旧作业的 main.cpp
因为我已经把旧文件删掉了,但是我没有在 VS 的项目管理器里面删掉
背景了解
要补全 rasterize_triangle()
于是看这个函数,输入的是 const Triangle& t
const 修饰函数形参,防止函数内部意外修改该形参
函数内部第一行
auto v = t.toVector4();
于是看这个是什么意思
函数定义是
std::array<Vector4f, 3> Triangle::toVector4() const
函数名后面写 const 表示该函数内不会修改对象数据成员
函数内部第一行用了一个没见过的数据类型:
std::array<Eigen::Vector4f, 3> res;
然后后面这个
std::transform(std::begin(v), std::end(v), res.begin(), [](auto& vec) { return Eigen::Vector4f(vec.x(), vec.y(), vec.z(), 1.f); });
std::transform 就是,对原数据每一个遍历,然后给一个新数组的 begin,就可以把结果写在新数组里
这个 v 是三角形内部的一个坐标,但是具体还不知道是什么坐标
class Triangle{
public:
Vector3f v[3]; /*the original coordinates of the triangle, v0, v1, v2 in counter clockwise order*/
v 在 setVertex 中被设置
void Triangle::setVertex(int ind, Vector3f ver){
v[ind] = ver;
}
setVertex 在 draw 函数中被使用
void rst::rasterizer::draw(pos_buf_id pos_buffer, ind_buf_id ind_buffer, col_buf_id col_buffer, Primitive type)
{
auto& buf = pos_buf[pos_buffer.pos_id];
auto& ind = ind_buf[ind_buffer.ind_id];
auto& col = col_buf[col_buffer.col_id];
float f1 = (50 - 0.1) / 2.0;
float f2 = (50 + 0.1) / 2.0;
Eigen::Matrix4f mvp = projection * view * model;
for (auto& i : ind)
{
Triangle t;
Eigen::Vector4f v[] = {
mvp * to_vec4(buf[i[0]], 1.0f),
mvp * to_vec4(buf[i[1]], 1.0f),
mvp * to_vec4(buf[i[2]], 1.0f)
};
//Homogeneous division
for (auto& vec : v) {
vec /= vec.w();
}
//Viewport transformation
for (auto & vert : v)
{
vert.x() = 0.5*width*(vert.x()+1.0);
vert.y() = 0.5*height*(vert.y()+1.0);
vert.z() = vert.z() * f1 + f2;
}
for (int i = 0; i < 3; ++i)
{
t.setVertex(i, v[i].head<3>());
//t.setVertex(i, v[i].head<3>());
//t.setVertex(i, v[i].head<3>());
}
其中很明显可以看到,一开始做了 MVP 变换,之后做了齐次坐标的变换,最后这个
for (auto & vert : v)
{
vert.x() = 0.5*width*(vert.x()+1.0);
vert.y() = 0.5*height*(vert.y()+1.0);
vert.z() = vert.z() * f1 + f2;
}
它实际上就是 NDC 坐标转屏幕坐标,而且还是屏幕上的像素点的中心的坐标
那么光栅化器中的 v 就是三角形每个顶点对应的屏幕上的像素点的中心的屏幕坐标
但是这个东西……他也不是整数的,他只是在以像素点中心组成的那个坐标系中
C++17 结构化绑定
auto [alpha, beta, gamma] = computeBarycentric2D(x, y, t.v);
这一句用到了 C++17 的结构化绑定的特性
因此需要将项目升级到 C++17
insideTriangle
一开始我写的 insideTriangle 不知道为什么是错的……
static bool insideTriangle(float x, float y, const Vector3f* _v)
{
// TODO : Implement this function to check if the point (x, y) is inside the triangle represented by _v[0], _v[1], _v[2]
Eigen::Vector3f n1(_v[1].x() - _v[0].x(), _v[1].y() - _v[0].y(), 0.0f);
Eigen::Vector3f n2(_v[2].x() - _v[1].x(), _v[2].y() - _v[1].y(), 0.0f);
Eigen::Vector3f n3(_v[0].x() - _v[2].x(), _v[0].y() - _v[2].y(), 0.0f);
Eigen::Vector3f p1(x - _v[0].x(), y - _v[0].y(), 0.0f);
Eigen::Vector3f p2(x - _v[1].x(), y - _v[1].y(), 0.0f);
Eigen::Vector3f p3(x - _v[2].x(), y - _v[2].y(), 0.0f);
float ans_z1 = p1.cross(n1).z();
float ans_z2 = p2.cross(n2).z();
float ans_z3 = p3.cross(n3).z();
std::cout << ans_z1 << ' ' << ans_z2 << ' ' << ans_z3 << std::endl;
if (ans_z1 > 0.0f && ans_z2 > 0.0f && ans_z3 > 0.0f) return true;
else return false;
}
我看别人写的作业,别人也是类似
https://blog.csdn.net/weixin_43940314/article/details/125209888
但是别人既判断三次叉乘结果都为正,又判断三次叉乘结果都为负,我就很迷惑,为什么呢,难道不是一定三次叉乘结果为正吗
于是我就打印了一下三次叉乘的结果,发现确实出现了三次叉乘结果为负的情况……
于是我也这么写,就能出现三角形了
static bool insideTriangle(float x, float y, const Vector3f* _v)
{
// TODO : Implement this function to check if the point (x, y) is inside the triangle represented by _v[0], _v[1], _v[2]
Eigen::Vector3f n1(_v[1].x() - _v[0].x(), _v[1].y() - _v[0].y(), 0.0f);
Eigen::Vector3f n2(_v[2].x() - _v[1].x(), _v[2].y() - _v[1].y(), 0.0f);
Eigen::Vector3f n3(_v[0].x() - _v[2].x(), _v[0].y() - _v[2].y(), 0.0f);
Eigen::Vector3f p1(x - _v[0].x(), y - _v[0].y(), 0.0f);
Eigen::Vector3f p2(x - _v[1].x(), y - _v[1].y(), 0.0f);
Eigen::Vector3f p3(x - _v[2].x(), y - _v[2].y(), 0.0f);
float ans_z1 = p1.cross(n1).z();
float ans_z2 = p2.cross(n2).z();
float ans_z3 = p3.cross(n3).z();
if (ans_z1 > 0.0f && ans_z2 > 0.0f && ans_z3 > 0.0f) return true;
else if (ans_z1 < 0.0f && ans_z2 < 0.0f && ans_z3 < 0.0f) return true;
else return false;
}
之后我想明白了……这个三角形确实,他的编号确实不一定是按照顺时针或者逆时针排序的……
虽然他注释里面写的是顺时针……
get_index
框架里面的 get_index 在 y 方向是相反的
int rst::rasterizer::get_index(int x, int y)
{
return (height-1-y)*width + x;
}
实际上,由于 OpenCV 也许是从左上到右下排列的,所以它可能用的是 (height-1-y)。这里就是把数字转换一下
三角形遮挡顺序
pdf 给的思路很清晰
//Screen space rasterization
void rst::rasterizer::rasterize_triangle(const Triangle& t) {
auto v = t.toVector4();
// TODO : Find out the bounding box of current triangle.
// iterate through the pixel and find if the current pixel is inside the triangle
// If so, use the following code to get the interpolated z value.
//auto[alpha, beta, gamma] = computeBarycentric2D(x, y, t.v);
//float w_reciprocal = 1.0/(alpha / v[0].w() + beta / v[1].w() + gamma / v[2].w());
//float z_interpolated = alpha * v[0].z() / v[0].w() + beta * v[1].z() / v[1].w() + gamma * v[2].z() / v[2].w();
//z_interpolated *= w_reciprocal;
// TODO : set the current pixel (use the set_pixel function) to the color of the triangle (use getColor function) if it should be painted.
// ndc to screen AABB
int x_screen_min = width - 1;
int x_screen_max = 0;
int y_screen_min = height - 1;
int y_screen_max = 0;
for (int i = 0; i < 3; i++) {
x_screen_min = std::min(x_screen_min, (int)v[i][0]);
y_screen_min = std::min(y_screen_min, (int)v[i][1]);
x_screen_max = std::max(x_screen_max, (int)v[i][0]);
y_screen_max = std::max(y_screen_max, (int)v[i][1]);
}
for (int x = x_screen_min; x <= x_screen_max; ++x) {
for (int y = y_screen_min; y <= y_screen_max; ++y) {
if (insideTriangle(x + 0.5f, y + 0.5f, t.v)) {
auto [alpha, beta, gamma] = computeBarycentric2D(x + 0.5f, y + 0.5f, t.v);
float w_reciprocal = 1.0 / (alpha / v[0].w() + beta / v[1].w() + gamma / v[2].w());
float z_interpolated = alpha * v[0].z() / v[0].w() + beta * v[1].z() / v[1].w() + gamma * v[2].z() / v[2].w();
z_interpolated *= w_reciprocal;
int index = get_index(x, y);
if (depth_buf[index] > z_interpolated) {
set_pixel(Vector3f(x, y, z_interpolated), t.getColor());
depth_buf[index] = z_interpolated;
}
}
}
}
}
但是他仍然在近裁面和远裁面用的是整数,因此最后得到的遮挡关系不对
https://games-cn.org/forums/topic/zuoyeer-sanjiaoxingfenkaidaopingmuliangcele/
https://games-cn.org/forums/topic/guanyuzuoye2lianggesanjiaoxingzhongdiebufendez-bufferwenti/
需要在 draw 这里改一下 f1 和 f2
void rst::rasterizer::draw(pos_buf_id pos_buffer, ind_buf_id ind_buffer, col_buf_id col_buffer, Primitive type)
{
auto& buf = pos_buf[pos_buffer.pos_id];
auto& ind = ind_buf[ind_buffer.ind_id];
auto& col = col_buf[col_buffer.col_id];
float f1 = -(50 - 0.1) / 2.0;
float f2 = -(50 + 0.1) / 2.0;
然后在 main 中也要改成负的
while(key != 27)
{
r.clear(rst::Buffers::Color | rst::Buffers::Depth);
r.set_model(get_model_matrix(angle));
r.set_view(get_view_matrix(eye_pos));
r.set_projection(get_projection_matrix(45, 1, -0.1, -50));
这样才能得到正确的遮挡关系
SSAA
https://zhuanlan.zhihu.com/p/425153734
-
4xSSAA,超级取样抗锯齿
每个像素维护一个4x子像素的颜色和深度列表
在子像素上进行所有的计算
最后在显示阶段,平均一下子像素,输出给显示器
-
4xMSAA,多重取样抗锯齿
每个像素维护一个4x子像素的颜色和深度列表
通过子像素的在三角形内的覆盖率对父像素颜色进行平均
最后在显示阶段,直接输出给显示器
一开始我写的 SSAA
//Screen space rasterization
void rst::rasterizer::rasterize_triangle(const Triangle& t) {
auto v = t.toVector4();
// TODO : Find out the bounding box of current triangle.
// iterate through the pixel and find if the current pixel is inside the triangle
// If so, use the following code to get the interpolated z value.
//auto[alpha, beta, gamma] = computeBarycentric2D(x, y, t.v);
//float w_reciprocal = 1.0/(alpha / v[0].w() + beta / v[1].w() + gamma / v[2].w());
//float z_interpolated = alpha * v[0].z() / v[0].w() + beta * v[1].z() / v[1].w() + gamma * v[2].z() / v[2].w();
//z_interpolated *= w_reciprocal;
// TODO : set the current pixel (use the set_pixel function) to the color of the triangle (use getColor function) if it should be painted.
// screen AABB
int x_screen_min = width - 1;
int x_screen_max = 0;
int y_screen_min = height - 1;
int y_screen_max = 0;
for (int i = 0; i < 3; i++) {
x_screen_min = std::min(x_screen_min, (int)v[i][0]);
y_screen_min = std::min(y_screen_min, (int)v[i][1]);
x_screen_max = std::max(x_screen_max, (int)v[i][0]);
y_screen_max = std::max(y_screen_max, (int)v[i][1]);
}
// SSAA var
std::vector<float> subsample_depth_buf;
std::vector<Eigen::Vector3f> subsample_frame_buf;
for (int x = x_screen_min; x <= x_screen_max; ++x) {
for (int y = y_screen_min; y <= y_screen_max; ++y) {
// SSAA var init
subsample_depth_buf.clear();
subsample_frame_buf.clear();
// SSAA
for (float delta_x = 0.25f; delta_x <= 0.75f; delta_x += 0.25f) {
for (float delta_y = 0.25f; delta_y <= 0.75f; delta_y += 0.25f) {
if (insideTriangle(x + delta_x, y + delta_y, t.v)) {
auto [alpha, beta, gamma] = computeBarycentric2D(x + delta_x, y + delta_y, t.v);
float w_reciprocal = 1.0 / (alpha / v[0].w() + beta / v[1].w() + gamma / v[2].w());
float z_interpolated = alpha * v[0].z() / v[0].w() + beta * v[1].z() / v[1].w() + gamma * v[2].z() / v[2].w();
z_interpolated *= w_reciprocal;
subsample_depth_buf.push_back(z_interpolated);
subsample_frame_buf.push_back(t.getColor());
}
}
}
// SSAA calc
int index = get_index(x, y);
float z_interpolated_sum = 0;
Eigen::Vector3f color_sum({ 0.0f, 0.0f, 0.0f });
if (subsample_depth_buf.size() > 0) {
for (float depth : subsample_depth_buf) {
z_interpolated_sum += depth;
}
for (Eigen::Vector3f color : subsample_frame_buf) {
color_sum += color;
}
z_interpolated_sum /= subsample_depth_buf.size();
color_sum /= 4.0f;
if (depth_buf[index] > z_interpolated_sum) {
set_pixel(Vector3f(x, y, z_interpolated_sum), color_sum);
depth_buf[index] = z_interpolated_sum;
}
}
}
}
}
得到了个全白的图……
之后发现是我循环写错了hhh,应该是以 0.5f 为步长的
于是写为
//Screen space rasterization
void rst::rasterizer::rasterize_triangle(const Triangle& t) {
auto v = t.toVector4();
// TODO : Find out the bounding box of current triangle.
// iterate through the pixel and find if the current pixel is inside the triangle
// If so, use the following code to get the interpolated z value.
//auto[alpha, beta, gamma] = computeBarycentric2D(x, y, t.v);
//float w_reciprocal = 1.0/(alpha / v[0].w() + beta / v[1].w() + gamma / v[2].w());
//float z_interpolated = alpha * v[0].z() / v[0].w() + beta * v[1].z() / v[1].w() + gamma * v[2].z() / v[2].w();
//z_interpolated *= w_reciprocal;
// TODO : set the current pixel (use the set_pixel function) to the color of the triangle (use getColor function) if it should be painted.
// screen AABB
int x_screen_min = width - 1;
int x_screen_max = 0;
int y_screen_min = height - 1;
int y_screen_max = 0;
for (int i = 0; i < 3; i++) {
x_screen_min = std::min(x_screen_min, (int)v[i][0]);
y_screen_min = std::min(y_screen_min, (int)v[i][1]);
x_screen_max = std::max(x_screen_max, (int)v[i][0]);
y_screen_max = std::max(y_screen_max, (int)v[i][1]);
}
// SSAA var
std::vector<float> subsample_depth_buf;
std::vector<Eigen::Vector3f> subsample_frame_buf;
for (int x = x_screen_min; x <= x_screen_max; ++x) {
for (int y = y_screen_min; y <= y_screen_max; ++y) {
// SSAA var init
subsample_depth_buf.clear();
subsample_frame_buf.clear();
// SSAA
for (float delta_x = 0.25f; delta_x <= 0.75f; delta_x += 0.5f) {
for (float delta_y = 0.25f; delta_y <= 0.75f; delta_y += 0.5f) {
if (insideTriangle(x + delta_x, y + delta_y, t.v)) {
auto [alpha, beta, gamma] = computeBarycentric2D(x + delta_x, y + delta_y, t.v);
float w_reciprocal = 1.0 / (alpha / v[0].w() + beta / v[1].w() + gamma / v[2].w());
float z_interpolated = alpha * v[0].z() / v[0].w() + beta * v[1].z() / v[1].w() + gamma * v[2].z() / v[2].w();
z_interpolated *= w_reciprocal;
subsample_depth_buf.push_back(z_interpolated);
subsample_frame_buf.push_back(t.getColor());
}
}
}
// SSAA calc
int index = get_index(x, y);
float z_sum = 0;
Eigen::Vector3f color_sum({ 0.0f, 0.0f, 0.0f });
if (subsample_depth_buf.size() > 0) {
for (float depth : subsample_depth_buf) {
z_sum += depth;
}
for (Eigen::Vector3f color : subsample_frame_buf) {
color_sum += color;
}
z_sum /= subsample_depth_buf.size();
color_sum /= 4.0f;
if (depth_buf[index] > z_sum) {
set_pixel(Vector3f(x, y, z_sum), color_sum);
depth_buf[index] = z_sum;
}
}
}
}
}
这个时候终于可以看到错误的黑边了……
根据别人的分析,这个黑实际上是因为原来的三角形中的颜色 /4.0f 了之后得到了深色
https://zhuanlan.zhihu.com/p/425153734
实际上不能在遍历每一个三角形的时候分成四个子像素的 subsample_depth_buf subsample_frame_buf,然后遍历下一个点的时候就清空 subsample_depth_buf subsample_frame_buf
而是应该把这个 subsample_depth_buf subsample_frame_buf 贯穿在若干次调用 rasterize_triangle() 之中
SSAA 不出现黑边的正确写法
光栅化器的头文件中添加全局的采样 buf
rasterizer.hpp
std::vector<Eigen::Vector3f> frame_buf;
std::vector<Eigen::Vector3f> subsample_frame_buf;
std::vector<float> subsample_depth_buf;
添加 SSAA 函数声明
void ssaa();
光栅化器中修改初始化函数和缓冲清零函数
这里删掉了原来的 depth_buf,不需要了
rasterizer.cpp
void rst::rasterizer::clear(rst::Buffers buff)
{
if ((buff & rst::Buffers::Color) == rst::Buffers::Color)
{
std::fill(frame_buf.begin(), frame_buf.end(), Eigen::Vector3f{0, 0, 0});
std::fill(subsample_frame_buf.begin(), subsample_frame_buf.end(), Eigen::Vector3f{ 0, 0, 0 });
}
if ((buff & rst::Buffers::Depth) == rst::Buffers::Depth)
{
std::fill(subsample_depth_buf.begin(), subsample_depth_buf.end(), std::numeric_limits<float>::infinity());
}
}
rst::rasterizer::rasterizer(int w, int h) : width(w), height(h)
{
frame_buf.resize(w * h);
subsample_frame_buf.resize(4 * w * h);
subsample_depth_buf.resize(4 * w * h);
}
光栅化每一个三角形时只计算 SSAA 相关的 buf
//Screen space rasterization
void rst::rasterizer::rasterize_triangle(const Triangle& t) {
auto v = t.toVector4();
// TODO : Find out the bounding box of current triangle.
// iterate through the pixel and find if the current pixel is inside the triangle
// If so, use the following code to get the interpolated z value.
//auto[alpha, beta, gamma] = computeBarycentric2D(x, y, t.v);
//float w_reciprocal = 1.0/(alpha / v[0].w() + beta / v[1].w() + gamma / v[2].w());
//float z_interpolated = alpha * v[0].z() / v[0].w() + beta * v[1].z() / v[1].w() + gamma * v[2].z() / v[2].w();
//z_interpolated *= w_reciprocal;
// TODO : set the current pixel (use the set_pixel function) to the color of the triangle (use getColor function) if it should be painted.
// screen AABB
int x_screen_min = width - 1;
int x_screen_max = 0;
int y_screen_min = height - 1;
int y_screen_max = 0;
for (int i = 0; i < 3; i++) {
x_screen_min = std::min(x_screen_min, (int)v[i][0]);
y_screen_min = std::min(y_screen_min, (int)v[i][1]);
x_screen_max = std::max(x_screen_max, (int)v[i][0]);
y_screen_max = std::max(y_screen_max, (int)v[i][1]);
}
for (int x = x_screen_min; x <= x_screen_max; ++x) {
for (int y = y_screen_min; y <= y_screen_max; ++y) {
int index = get_index(x, y);
int sub_idx = 0;
// SSAA
for (float delta_x = 0.25f; delta_x <= 0.75f; delta_x += 0.5f) {
for (float delta_y = 0.25f; delta_y <= 0.75f; delta_y += 0.5f) {
if (insideTriangle(x + delta_x, y + delta_y, t.v)) {
auto [alpha, beta, gamma] = computeBarycentric2D(x + delta_x, y + delta_y, t.v);
float w_reciprocal = 1.0 / (alpha / v[0].w() + beta / v[1].w() + gamma / v[2].w());
float z_interpolated = alpha * v[0].z() / v[0].w() + beta * v[1].z() / v[1].w() + gamma * v[2].z() / v[2].w();
z_interpolated *= w_reciprocal;
subsample_depth_buf.push_back(z_interpolated);
subsample_frame_buf.push_back(t.getColor());
if (subsample_depth_buf[4 * index + sub_idx] > z_interpolated) {
subsample_frame_buf[4 * index + sub_idx] = t.getColor();
subsample_depth_buf[4 * index + sub_idx] = z_interpolated;
}
}
++sub_idx;
}
}
}
}
}
在 ssaa() 中计算抗锯齿之后得到的 frame_buf
void rst::rasterizer::ssaa() {
Eigen::Vector3f color_sum({ 0.0f, 0.0f, 0.0f });
for (int i = 0; i < width * height; ++i) {
color_sum = { 0.0f, 0.0f, 0.0f };
for (int j = 0; j < 4; ++j) {
color_sum += subsample_frame_buf[4 * i + j];
}
frame_buf[i] = color_sum / 4.0f;
}
}
在 draw() 函数中,在光栅化各个三角形结束之后,SSAA
rasterize_triangle(t);
}
ssaa();
}
结果:
看上去不错哈
Lecture 8 Shading 2
Blinn-Phong 反射光模型 续
要得到一张图,就要在不同地方多次着色,这就引出了着色频率的问题
漫反射项
复习上一节
L d = k d I r 2 max ( 0 , n ⋅ l ) L_d = k_d \dfrac{I}{r^2}\max{(0, \mathbf{n} \cdot \mathbf{l})} Ld=kdr2Imax(0,n⋅l)
其中 k d k_d kd 是漫反射系数,物理意义与颜色相关, L d L_d Ld 表示漫反射光强, n \mathbf{n} n 表示着色点法向, l \mathbf{l} l 表示光源方向
高光项
设光的反射方向为 R R R,那么又根据高光只能在一定角度看到的原理,认为高光项是镜面反射造成的
而镜面反射的意义,我们可以认为是,高光项在 R \mathbf R R 附近有一个分布
那么人如果能看到镜面反射光,说明光的反射方向 R \mathbf R R 与人眼观测方向 v \mathbf v v 很接近
那么我们如果要判断 R \mathbf R R 和 v \mathbf v v 是否接近的话,那就是要求 R \mathbf R R 嘛,那就是要用光的入射方向 I \mathbf I I 和着色点的法向方向 n \mathbf n n 来计算 R \mathbf R R
硬要计算也不是不行,但是也可以用其他方法计算
比如我们可以计算半程向量 h \mathbf h h,它是光的入射方向 I \mathbf I I 与人眼观测方向 v \mathbf v v 之间的角平分线
h = b i s e c t o r ( v , I ) = v + I ∣ ∣ v + I ∣ ∣ \mathbf h = bisector(\mathbf v, \mathbf I) \\ = \dfrac{\mathbf v + \mathbf I}{||\mathbf v + \mathbf I||} h=bisector(v,I)=∣∣v+I∣∣v+I
这个计算本质上就是平行四边形法则,两个相等的向量相加得到这两个向量的角平分线,然后再归一化
那么高光项计算公式为
L s = k s ( I / r 2 ) max ( 0 , cos α ) p = k s ( I / r 2 ) max ( 0 , n ⋅ h ) p L_s = k_s (I/r^2) \max(0, \cos\alpha)^p \\ = k_s (I/r^2) \max(0, \mathbf n \cdot \mathbf h)^p Ls=ks(I/r2)max(0,cosα)p=ks(I/r2)max(0,n⋅h)p
其中 k s k_s ks 是高光系数, L s L_s Ls 是高光项光强
原先要判断光的反射方向 R \mathbf R R 与人眼观测方向 v \mathbf v v 接近程度,现在判断着色点的法向方向 n \mathbf n n 与半程向量 h \mathbf h h 接近程度
在 cos 上面加指数 p 是因为一般的 cos 的容忍度很高,比如 cos 的一次幂,在 0 到 90 度的范围内,值都是可观的
高光项夹角近似之后得到的夹角与原来的夹角之间的关系
Blinn-Phong 用
高光计算公式相关的能量损失
在高光计算公式中也可以加上一个能量损失项,与光的入射方向 I \mathbf I I 和着色点的法向方向 n \mathbf n n 相关
但是 Blinn-Phong 毕竟是经验模型,可以简化
我只需要保证我能看到高光
Phong 与 Blinn-Phong
使用光的反射方向 R \mathbf R R 与人眼观测方向 v \mathbf v v 接近程度来计算高光,就是 Phong 模型
使用着色点的法向方向 n \mathbf n n 与半程向量 h \mathbf h h 接近程度来计算高光,就是 Blinn-Phong 模型
Blinn-Phong 模型是对 Phong 模型的改正,因为半程向量好算
环境光
认为来自环境的光是常量
L a = k a I a L_a = k_a I_a La=kaIa
k a k_a ka 是环境光系数, I a I_a Ia 是常数, L a L_a La 是环境光光强
那么其实本质上就是颜色
如果要精确计算环境光,就要涉及到全局光照的知识
能量?离得远觉得暗?人眼到物体的距离为什么不考虑?
之后说
着色频率
着色应用在哪些点
逐面着色 Flat Shading
每一个顶点有自己的法线,逐顶点着色,然后在面内对颜色插值 Gouraud Shading
由顶点法线插值,得到每一个像素的法线,逐像素着色 Phong Shading
如果模型的面数高的话,那么模型的着色频率低,比如使用逐面着色也可能得到好的结果
因此模型的着色频率与模型的面数有关
Blinn-Phong 模型 != Phong Shading
一个是模型,一个是逐像素着色 Shading
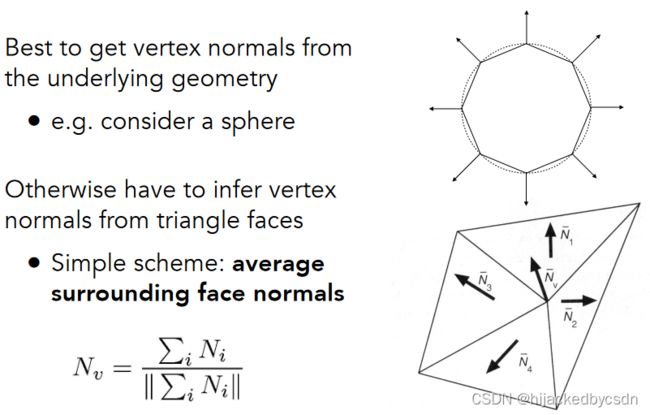
怎么计算顶点的法线
假设要计算法线的顶点实际上是球上的顶点
如果是球上的顶点,那么计算法线就很简单,直接是从球心指向顶点
对于实际物体中的顶点,认为某一点的法线是这个顶点所关联的所有面的法线的平均值
怎么计算逐像素的法线
使用重心坐标
图形管线
从模型到屏幕图像
输入:三维空间(模型空间)中的顶点
经过 MVP 变换,得到屏幕空间中的顶点
将屏幕空间中的顶点连接成三角形
将屏幕空间中的三角形通过光栅化得到片元
对片元通过片元着色器,Z-Buffer,Shading
对片元缓冲经过模板测试,输出图像

如果 Shading 是逐顶点着色,那么 Shading 就在 Vertex Peocessing 和 FrameBuffer Operations 都发生
如果是逐像素着色,那么就是要等到像素都产生了之后在像素中做

可编程的部分在 Vertex Processing 和 Fragment Processing,顶点着色器和片元着色器
纹理映射
任何一个三维物体的表面都是二维的
如果是多个物体,那么多个物体的表面展开还是平面
既然可以展开,就可以映射
三角形每一个顶点都有一个 UV
Lecture 9: Shading 3 (Texture Mapping cont)
插值
已知三角形顶点都有某个属性,想要在三角形内部插值这个属性
重心坐标

已知三角形三个点的坐标为 A , B , C A,B,C A,B,C
那么三角形所在的平面上的任意一点的坐标可以用这三个点来表示
这样为什么是成立的?因为本质上,三角形三个点就确定了两个基向量,比如 AB,AC,这两个基向量就可以确定一个平面
那么对这两个基向量的系数怎么写都无所谓
既然是无所谓的,那么就可以把 AB,AC 的线性组合变成 B-A,C-A 的线性组合,最后变成 A,B,C 的线性组合
那么最终得到三角形所在的平面上的任意一点的坐标的表达式为
( x , y ) = α A + β B + γ C (x,y) = \alpha A + \beta B + \gamma C (x,y)=αA+βB+γC
其中约定 α + β + γ = 1 \alpha + \beta + \gamma = 1 α+β+γ=1
如果要表示该点在三角形内部,那么需要
α > 0 , β > 0 , γ > 0 \alpha > 0, \\ \beta > 0, \\ \gamma > 0 α>0,β>0,γ>0
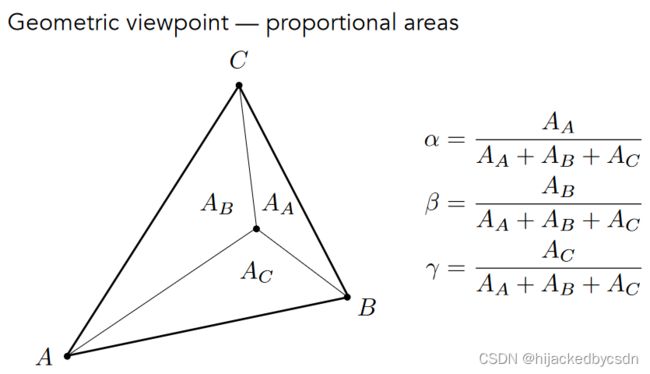
重心坐标的计算
重心坐标可以通过子三角形的面积计算出来
而三角形面积就是构成三角形的两个向量的叉乘的标量值,因此得到
为啥?因为 ∣ n 1 × n 2 ∣ = ∣ n 1 ∣ ∣ n 2 ∣ sin < n 1 , n 2 > |\mathbf{n_1} \times \mathbf{n_2}| = |\mathbf{n_1}||\mathbf{n_2}|\sin<\mathbf{n_1},\mathbf{n_2}> ∣n1×n2∣=∣n1∣∣n2∣sin<n1,n2> 其中一个向量的长度乘以 sin 就是另外一个向量上的高
还有一种推导方法是,不从面积这个意义入手,而是用消元的办法
 来自:https://blog.csdn.net/Q_pril/article/details/123598746
来自:https://blog.csdn.net/Q_pril/article/details/123598746
重心坐标在投影操作之后会变化
因为投影之后会变化,所以我们在三角形中插值某个属性的时候,我们应该是在原始的坐标中插值,而不是在 MVP 之后的坐标中插值
那么但是我们一般得到的都是 MVP 之后的坐标,所以我们这里在插值的时候还需要逆变换回去
纹理采样
for each rasterized screen sample (x, y):
(u, v) = evaluate texture coordinate ar (x, y);
texcolor = texture.sample(u, v);
set sample's color to texcolor;
高分辨率的物体,去采样低分辨率的纹理
高分辨率的物体,去采样低分辨率的纹理
Nearest 采样最近像素:使用较多,锯齿明显。只采样u11。
Bilinear 双线性插值:使用较多,锯齿较少。需要采样4个粉红色的点u00~u11。
Bicubic 双三次插值:使用较少,锯齿较少。除了4个粉红色点外,还需要每边向外多采样一个点,即4x4=16个点。
双线性插值
高分辨率的物体采样低分辨率的纹理,就会出现采样非整数纹理点的情况
假设我们要对一个非整数点进行插值
那么取它临近的四个整数点
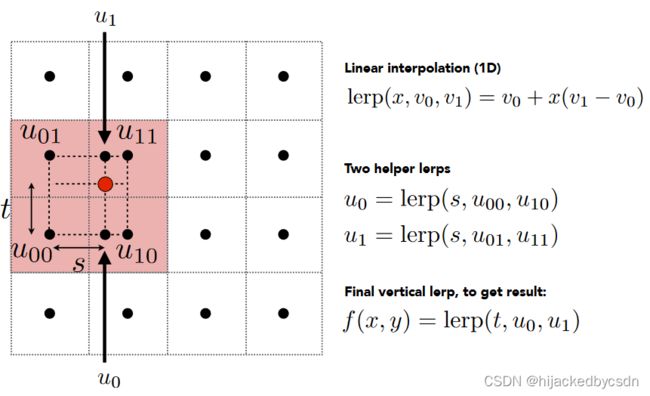
可以对 x 方向上,底部的两个整数点做插值,比例为 s,得到 u 0 u_0 u0,顶部的两个整数点做插值,比例为 s,得到 u 1 u_1 u1
最后在 y 方向上,对 u 0 , u 1 u_0, u_1 u0,u1 插值,比例为 t,得到 f ( x , y ) f(x,y) f(x,y)
低分辨率的物体,去采样高分辨率的纹理
近处会出现锯齿,远处会出现摩尔纹
纹理的采样范围大小
左边相当于 高分辨率的物体,去采样低分辨率的纹理
也就是一个单位面积的片元对应到纹理上采样很小范围
右边相当于 低分辨率的物体,去采样高分辨率的纹理
也就是一个单位面积的片元对应到纹理上采样很大范围
这里的单位面积的片元指的是屏幕空间上的单位面积,就是说,屏幕空间上的单位面积,如果是在距离镜头比较近的模型上,那么就占据了这个模型的纹理的一小部分;如果是在距离镜头比较远的模型上,那么就占据了这个模型的纹理的很大部分(假设这两个模型用的同一张纹理)
如果对应的采样范围小,我们可以用双线性插值作为采样的值
如果对应的采样范围大,假设我们取这个采样范围的中心距离最近的那个整数纹理像素点的颜色作为这个采样范围的颜色,这时就会出现问题
从之前提到的频率的角度分析,如果用一个很大的范围去采样频率,在这一个范围内,纹理有很多纹理像素点,颜色变化很快,相当于一个高频的信号,而采样率低
那就是我需要在这个大的采样范围内有很多个采样点,再对这些采样点的结果做平均
但是用多个采样点会让性能倍增
但是如果不采样呢?
如果给定一个点,立即能够得到这个点对应的采样大范围内的平均值,就相当于不用采样了
就,本身我最终都是要得到一个平均值,但是我现在如果得到平均值的方法不是通过对每一个点都密集增加子采样点,而是通过数据结构,直接计算范围内的平均值,就可能避免增加子采样点这个方法的性能问题
范围查询的方式 Mipmap
前面提到,在纹理采样范围很大的时候,需要快速知道这个大范围内的各个像素点的近似平均值
为了避免增加子采样点这个方法的性能问题,需要有一个方法快速范围查询
对应到图像中,这个数据结构就是 Mipmap
Mipmap 只能做近似的正方形的范围查询
MipMap 所占空间是多少?
1/4, (1/4)^2,…求和得 1/3
所占空间是原图的 1/3
方便理解的,可以把每一次生成的 Mipmap 复制三份,摆在三个位置上
怎么知道片元中一个像素对应纹理上的多大的采样点
我们已经通过插值知道片元中每一个像素点的 UV 坐标

片元中的像素点移动到另外一个像素点,移动距离是 (dx, dy),对应到 UV 坐标系中,UV 变化量是 (du, dv)
那么表示采样范围的长度 L = max ( ( d u d x ) 2 + ( d v d x ) 2 , ( d u d y ) 2 + ( d v d y ) 2 ) L=\max(\sqrt{(\dfrac{\mathrm{d}u}{\mathrm{d}x})^2 + (\dfrac{\mathrm{d}v}{\mathrm{d}x})^2},\sqrt{(\dfrac{\mathrm{d}u}{\mathrm{d}y})^2 + (\dfrac{\mathrm{d}v}{\mathrm{d}y})^2}) L=max((dxdu)2+(dxdv)2,(dydu)2+(dydv)2)
本次采样要使用的 Mipmap 的等级 D = log 2 L D = \log_2{L} D=log2L
这里的 D D D 是取整之后的

这里算出 L L L 之后,就认为这个采样点在纹理中的采样范围是一个边长为 L L L 的正方形
这样做的好处是,与 Mipmap 对应起来,例如 L = 1 L = 1 L=1 是对应原图, L = 2 L = 2 L=2 时对应缩小了一倍的 Mipmap……刚好在 level = i 的 Mipmap 的某一点的像素值的物理意义就是边长为 i 的在原图上的正方形的平均值
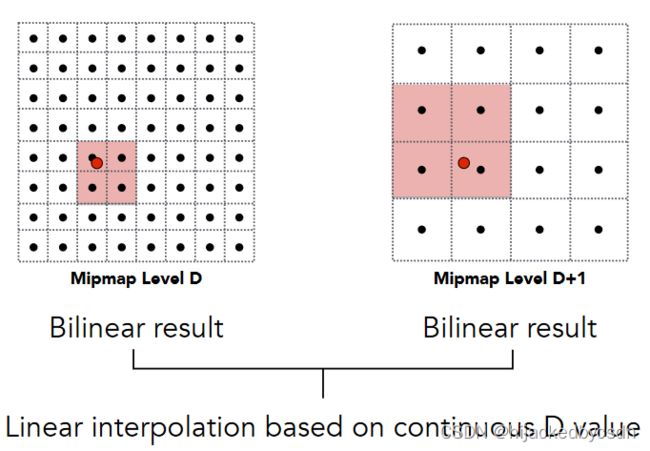
不同 level 的 Mipmap 之间的插值:三线性插值
当计算得到的 level 为非整数的时候,在两个整数 level 的 Mipmap 中,各自有一次插值,在两个整数 level 的 Mipmap 的插值结果之间,以非整数 level 的小数部分作为比例,再进行一次插值
这就叫做三线性插值
各向异性过滤
如果对应的采样范围大,假设我们取这个采样范围的中心距离最近的那个整数纹理像素点的颜色作为这个采样范围的颜色,这时就会出现问题
或者……原视频也没说具体选择那个采样点来代表这个采样范围,但是总是就是只选一个点

如果取一个范围的平均,比如使用多个子采样点,然后求这些子采样点的平均,可以得到好的效果,但是有性能问题
假设这样的图应该是正确的效果
如果使用 Mipmap 获得到这样的效果
比如我们近似使用一个正方形来代表片元中的某一个像素点对应到 UV 中的采样范围,还有三线性插值本身也是一个近似行为
如果使用各向异性过滤,情况会好很多
首先看 Mipmap 为什么会错

屏幕空间中的片元的单位面积可能对应到 UV 空间中是一个狭长的矩形
而可能出现的情况是,在这个 UV 点上,只有使用这个真实的,狭长的矩形,才能获得那个狭长的范围内的颜色,而如果使用一个矩形包围盒来代替,在这个矩形范围内的颜色分布跟狭长矩阵内的颜色分布是不一样的,一般的话,更大的范围可能就会过度模糊,所以得到的颜色平均值会有较大的偏差
各向异性过滤可以查询水平或者竖直放置的矩形,但是对于斜着的矩形仍然无能为力

各向异性过滤使用的 Mipmap 的空间消耗是原 Mipmap 的三倍
各向异性过滤也称为 Ripmap
EWA 过滤
对于斜着的矩形用多个圆来采样
作业 3
在计算齐次坐标的归一化时保留深度
作业 1 和作业 2 中写的关于齐次坐标的变换,都是 vec /= vec.w();
void rst::rasterizer::draw(pos_buf_id pos_buffer, ind_buf_id ind_buffer, col_buf_id col_buffer, Primitive type)
{
auto& buf = pos_buf[pos_buffer.pos_id];
auto& ind = ind_buf[ind_buffer.ind_id];
auto& col = col_buf[col_buffer.col_id];
float f1 = -(50 - 0.1) / 2.0;
float f2 = -(50 + 0.1) / 2.0;
Eigen::Matrix4f mvp = projection * view * model;
for (auto& i : ind)
{
Triangle t;
Eigen::Vector4f v[] = {
mvp * to_vec4(buf[i[0]], 1.0f),
mvp * to_vec4(buf[i[1]], 1.0f),
mvp * to_vec4(buf[i[2]], 1.0f)
};
// Homogeneous division
for (auto& vec : v) {
vec /= vec.w();
}
...
但是作业 3 中更正了这里
void rst::rasterizer::draw(std::vector<Triangle *> &TriangleList) {
float f1 = (50 - 0.1) / 2.0;
float f2 = (50 + 0.1) / 2.0;
Eigen::Matrix4f mvp = projection * view * model;
for (const auto& t:TriangleList)
{
Triangle newtri = *t;
std::array<Eigen::Vector4f, 3> mm {
(view * model * t->v[0]),
(view * model * t->v[1]),
(view * model * t->v[2])
};
std::array<Eigen::Vector3f, 3> viewspace_pos;
std::transform(mm.begin(), mm.end(), viewspace_pos.begin(), [](auto& v) {
return v.template head<3>();
});
Eigen::Vector4f v[] = {
mvp * t->v[0],
mvp * t->v[1],
mvp * t->v[2]
};
// Homogeneous division
// keep vec.w() same
// because vec.w() is z value of origin point in MV space
// why vec.w() is z value?
// because p2o matrix in get_projection_matrix()
// p2o * (x, y, z, 1) = (n * x, n * y, (n + f) * z - n * f, z)
for (auto& vec : v) {
vec.x()/=vec.w();
vec.y()/=vec.w();
vec.z()/=vec.w();
}
为什么作业 3 中会这么改呢,他主要是希望保留 w 值不要变成 1
虽然这样得到的是一个奇怪的 ( n x / z , n y / z , n + f − n f / z , z ) (nx/z,ny/z,n+f-nf/z,z) (nx/z,ny/z,n+f−nf/z,z) 而不是正确的 ( n x / z , n y / z , n + f − n f / z , 1 ) (nx/z,ny/z,n+f-nf/z,1) (nx/z,ny/z,n+f−nf/z,1)
但是他这里主要是因为想要使用这个正确的 z 用来做 z-buffer
他做 z-buffer 的时候是
auto [alpha, beta, gamma] = computeBarycentric2D(x + delta_x, y + delta_y, t.v);
float w_reciprocal = 1.0 / (alpha / v[0].w() + beta / v[1].w() + gamma / v[2].w());
float z_interpolated = alpha * v[0].z() / v[0].w() + beta * v[1].z() / v[1].w() + gamma * v[2].z() / v[2].w();
z_interpolated *= w_reciprocal;
如果是在齐次的时候 vec /= vec.w();,那么每个 v[i] 的 .w() 都是 1 了,没有深度的意义了
所以要改
当然像对于作业 2 中那样简单的例子,我们反而看不出什么差别
那这样的话,我其实看不出来他这个三角形里面的 toVector4() 有什么用……所以我之后就不用这个函数了
重心坐标
自己写的重心坐标计算
原来的重心坐标计算公式
static std::tuple<float, float, float> computeBarycentric2D(float x, float y, const Vector4f* v){
float c1 = (x*(v[1].y() - v[2].y()) + (v[2].x() - v[1].x())*y + v[1].x()*v[2].y() - v[2].x()*v[1].y()) / (v[0].x()*(v[1].y() - v[2].y()) + (v[2].x() - v[1].x())*v[0].y() + v[1].x()*v[2].y() - v[2].x()*v[1].y());
float c2 = (x*(v[2].y() - v[0].y()) + (v[0].x() - v[2].x())*y + v[2].x()*v[0].y() - v[0].x()*v[2].y()) / (v[1].x()*(v[2].y() - v[0].y()) + (v[0].x() - v[2].x())*v[1].y() + v[2].x()*v[0].y() - v[0].x()*v[2].y());
float c3 = (x*(v[0].y() - v[1].y()) + (v[1].x() - v[0].x())*y + v[0].x()*v[1].y() - v[1].x()*v[0].y()) / (v[2].x()*(v[0].y() - v[1].y()) + (v[1].x() - v[0].x())*v[2].y() + v[0].x()*v[1].y() - v[1].x()*v[0].y());
return {c1,c2,c3};
}
虽然简练,但是我根本不想去看具体的公式对不对
刚好这节课讲了重心坐标,所以我写成:
static std::tuple<float, float, float> computeBarycentric2D(float x, float y, const Vector4f* v){
Eigen::Vector2f p(x, y);
Eigen::Vector2f tri_node_coords[3];
for (int i = 0; i < 3; ++i) {
tri_node_coords[i] = v[i].head<2>();
}
Eigen::Vector2f edge_1, edge_2;
float s_sub_tri[3];
for (int i = 0; i < 3; ++i) {
edge_1 = tri_node_coords[(i + 1) % 3] - p;
edge_2 = tri_node_coords[(i + 2) % 3] - p;
s_sub_tri[i] = edge_1.x()* edge_2.y() - edge_2.x() * edge_1.y();
}
float s_sum = 0;
for (int i = 0; i < 3; ++i) {
s_sum += s_sub_tri[i];
}
return { s_sub_tri[0] / s_sum, s_sub_tri[1] / s_sum, s_sub_tri[2] / s_sum };
}
我自己测试了一下,得到的结果是一样的
#include 原来的重心坐标在计算的时候可能计算出超出 [0, 1] 的 UV
之后在算 texture_fragment_shader 的时候,因为出错了,所以为了 Debug 换成了原来的重心坐标试试
结果试出来反而出现了超出 [0, 1] 的 UV 的错误
搜了一下,别人也是这样的,也没有什么好的解决方法……
Eigen::Vector3f getColor(float u, float v)
{
if (u < 0) u = 0;
if (u > 1) u = 1;
if (v < 0) v = 0;
if (v > 1) v = 1;
auto u_img = u * width;
auto v_img = (1 - v) * height;
auto color = image_data.at<cv::Vec3b>(v_img, u_img);
return Eigen::Vector3f(color[0], color[1], color[2]);
}
但我用我自己的重心坐标计算公式就不会有这个问题
所以我感觉我还是自己的计算出错了……
于是我在 UV 超出 [0,1] 的时候测试一下我算的跟他是不是一样的
自己写的 computeBarycentric2D 跟原版的不一样
测试 1:
其中 computeBarycentric2D 是我写的,computeBarycentric2D_2 是原版
if (depth_buf[index] > zp) {
// todo: interpolate
interpolated_color = interpolate(alpha, beta, gamma, t.color[0], t.color[1], t.color[2], 1.0f);
interpolated_normal = interpolate(alpha, beta, gamma, t.normal[0], t.normal[1], t.normal[2], 1.0f).normalized();
interpolated_texcoords = interpolate(alpha, beta, gamma, t.tex_coords[0], t.tex_coords[1], t.tex_coords[2], 1.0f);
auto [alpha_2, beta_2, gamma_2] = computeBarycentric2D_2(x + 0.5f, y + 0.5f, t.v);
Eigen::Vector2f interpolated_texcoords_2 = interpolate(alpha_2, beta_2, gamma_2, t.tex_coords[0], t.tex_coords[1], t.tex_coords[2], 1.0f);
if (interpolated_texcoords_2.x() > 1.0f || interpolated_texcoords_2.y() > 1.0f) {
std::cout << alpha << ' ' << beta << ' ' << gamma << ' ' << std::endl;
std::cout << alpha_2 << ' ' << beta_2 << ' ' << gamma_2 << ' ' << std::endl;
std::cout << interpolated_texcoords << std::endl;
std::cout << interpolated_texcoords_2 << std::endl;
std::cout << "----------------------------------" << std::endl;
}
interpolated_shadingcoords = interpolate(alpha, beta, gamma, view_pos[0], view_pos[1], view_pos[2], 1.0f);
// pass to frag shader
fragment_shader_payload payload(interpolated_color, interpolated_normal.normalized(), interpolated_texcoords, texture ? &*texture : nullptr);
payload.view_pos = interpolated_shadingcoords;
auto pixel_color = fragment_shader(payload);
// update buffer
set_pixel(Vector2i(x, y), pixel_color);
depth_buf[index] = zp;
}
结果发现我们真的不是一样的……
输出:
8.9596 -2.00381 -5.9558
9.28571 -1.75 -5.375
0.190906
0.46933
0.371823
1.00153
测试 2:
if (insideTriangle(x + 0.5f, y + 0.5f, t.v)) {
auto [alpha, beta, gamma] = computeBarycentric2D(x + 0.5f, y + 0.5f, t.v);
auto [alpha_2, beta_2, gamma_2] = computeBarycentric2D_2(x + 0.5f, y + 0.5f, t.v);
if (std::abs(alpha - alpha_2) > 0.1f) {
std::cout << "----------------------------------" << std::endl;
std::cout << alpha << ' ' << alpha_2 << std::endl;
}
if (std::abs(beta - beta_2) > 0.1f) {
std::cout << beta << ' ' << beta_2 << std::endl;
}
if (std::abs(gamma - gamma_2) > 0.1f) {
std::cout << gamma << ' ' << gamma_2 << std::endl;
}
输出:
----------------------------------
15.2949 15.0455
-7.22579 -7.42857
-7.06913 -6.90909
----------------------------------
-6.64221 -6.31579
8.40994 8.05263
-0.767736 -0.882353
3.1118 3.23529
----------------------------------
10.8876 10.4
-4.34007 -4.1
-2.85846 -2.96
1.65415 1.77778
-3.23407 -3.35294
----------------------------------
8.9596 9.28571
-2.00381 -1.75
-5.9558 -5.375
----------------------------------
-5.86862 -5.71429
----------------------------------
-7.93346 -7.83333
----------------------------------
-4.57373 -4.70588
----------------------------------
-4.27347 -4.45833
这样看上去,我写的和原版的都会出现,重心坐标为负的情况
从这里也可以看出,这个重心坐标为负,既存在两个坐标为正一个坐标为负的情况,又存在两个坐标为负一个坐标为正的情况
出现负的重心坐标是合理的,因为点可能位于三角形边上
但是如果我要是把这些负的重心坐标给去掉的话
比如把 rasterize_triangle() 中计算颜色缓存的内层中加一个重心坐标的判断
for (int x = x_screen_min; x <= x_screen_max; ++x) {
for (int y = y_screen_min; y <= y_screen_max; ++y) {
if (insideTriangle(x + 0.5f, y + 0.5f, t.v)) {
auto [alpha, beta, gamma] = computeBarycentric2D(x + 0.5f, y + 0.5f, t.v);
if (alpha < 0.0f || alpha > 1.0f) continue;
if (beta < 0.0f || beta > 1.0f) continue;
if (gamma < 0.0f || gamma > 1.0f) continue;
得到的渲染结果像这样:
可见,重心坐标为负对应着点位于三角形边上的特殊情况
我在相关帖子的回答:
https://games-cn.org/forums/topic/%e8%af%b7%e6%95%99%e8%80%81%e5%b8%88%e4%b8%80%e4%b8%aa%e9%97%ae%e9%a2%98%ef%bc%8c%e5%85%b3%e4%ba%8e%e9%87%8d%e5%bf%83%e5%9d%90%e6%a0%87/#post-16631
所以我们不需要考虑去掉那些重心坐标为负的点,因为重心坐标为负的点也可能位于三角形的边上
如果去掉了这些点,就相当于在三角形的边上没有颜色,那么渲染出来的就会在模型的每一个三角面的边上显示出缝隙
所以只要你的 insideTriangle() 写对了,就不需要考虑 computeBarycentric2D() 算出来的重心坐标为负还是为正
透视矫正的公式推导与对应代码写法
仍然是看 https://blog.csdn.net/Q_pril/article/details/123598746
观察空间中的 Z
Z = ( Z 1 Z 2 Z 3 ) ( α β γ ) Z = \left (\begin{array}{cccc} Z_1 & Z_2 & Z_3 \end{array}\right) \left (\begin{array}{cccc} \alpha \\ \beta \\ \gamma \end{array}\right) Z=(Z1Z2Z3) αβγ
如果不校正的话,算到的 Z’ 是这样的
Z ′ = ( Z 1 ′ Z 2 ′ Z 3 ′ ) ( α ′ β ′ γ ′ ) Z' = \left (\begin{array}{cccc} Z'_1 & Z'_2 & Z'_3 \end{array}\right) \left (\begin{array}{cccc} \alpha' \\ \beta' \\ \gamma' \end{array}\right) Z′=(Z1′Z2′Z3′) α′β′γ′
但是我们不想要这个 Z’
对于我们而言,有意义的量是 Z 1 ′ , Z 2 ′ , Z 3 ′ Z'_1, Z'_2, Z'_3 Z1′,Z2′,Z3′ 因为我们是从屏幕这里看过来的,所以我们需要的深度值是屏幕空间中的深度值
但是我们需要的重心坐标是观察空间中的重心坐标,因为从模型空间到观察空间中都没有发生缩放,只有旋转和平移,物体是没有变形的;而投影之后物体就有变形了,所以不能取投影空间中的
我们要得到的是没有变形的空间中的重心坐标
因此我们要的是 α , β , γ \alpha, \beta, \gamma α,β,γ 而不是 α ′ , β ′ , γ ′ \alpha', \beta', \gamma' α′,β′,γ′
但是我们现在如果只知道屏幕空间中的着色点 ( x , y ) (x,y) (x,y) 和屏幕空间中的三角形的顶点坐标,那么我们就是只能算出屏幕空间中的三角形的重心坐标
所以要想一个方法从 α ′ , β ′ , γ ′ \alpha', \beta', \gamma' α′,β′,γ′ 得到 α , β , γ \alpha, \beta, \gamma α,β,γ
(当然这个思路,是我看了别人写的整个过程之后才想到的,似乎有点马后炮了hh
对 Z 变形
Z = 1 ⋅ Z = ( α ′ + β ′ + γ ′ ) ⋅ Z = ( Z 1 Z 1 α ′ + Z 2 Z 2 β ′ + Z 3 Z 3 γ ′ ) ⋅ Z = ( Z 1 Z 2 Z 3 ) ( Z Z 1 α ′ Z Z 2 β ′ Z Z 3 γ ′ ) Z = 1 \cdot Z \\ = (\alpha' + \beta' + \gamma') \cdot Z \\ = (\dfrac{Z_1}{Z_1}\alpha' + \dfrac{Z_2}{Z_2}\beta' + \dfrac{Z_3}{Z_3}\gamma') \cdot Z \\ = \left (\begin{array}{cccc} Z_1 & Z_2 & Z_3 \end{array}\right) \left (\begin{array}{cccc} \dfrac{Z}{Z_1}\alpha' \\ \dfrac{Z}{Z_2}\beta' \\ \dfrac{Z}{Z_3}\gamma' \end{array}\right) Z=1⋅Z=(α′+β′+γ′)⋅Z=(Z1Z1α′+Z2Z2β′+Z3Z3γ′)⋅Z=(Z1Z2Z3) Z1Zα′Z2Zβ′Z3Zγ′
由观测空间中的 Z 的定义,有
α = Z Z 1 α ′ β = Z Z 2 β ′ γ = Z Z 3 γ ′ \alpha = \dfrac{Z}{Z_1}\alpha' \\ \beta = \dfrac{Z}{Z_2}\beta' \\ \gamma = \dfrac{Z}{Z_3}\gamma' α=Z1Zα′β=Z2Zβ′γ=Z3Zγ′
又因为 α + β + γ = 1 \alpha + \beta + \gamma = 1 α+β+γ=1,得
Z Z 1 α ′ + Z Z 2 β ′ + Z Z 3 γ ′ = 1 \dfrac{Z}{Z_1}\alpha' + \dfrac{Z}{Z_2}\beta' + \dfrac{Z}{Z_3}\gamma' = 1 Z1Zα′+Z2Zβ′+Z3Zγ′=1
提取 Z Z Z 有
Z = 1 / ( 1 Z 1 α ′ + 1 Z 2 β ′ + 1 Z 3 γ ′ ) Z = 1/(\dfrac{1}{Z_1}\alpha' + \dfrac{1}{Z_2}\beta' + \dfrac{1 }{Z_3}\gamma') Z=1/(Z11α′+Z21β′+Z31γ′)
对应到代码中
float Z = 1.0 / (alpha / t.v[0].w() + beta / t.v[1].w() + gamma / t.v[2].w());
这一句算的就是
Z = 1 / ( 1 Z 1 α ′ + 1 Z 2 β ′ + 1 Z 3 γ ′ ) Z = 1/(\dfrac{1}{Z_1}\alpha' + \dfrac{1}{Z_2}\beta' + \dfrac{1 }{Z_3}\gamma') Z=1/(Z11α′+Z21β′+Z31γ′)
因为前面在计算透视变换之后,在齐次坐标归一化的时候,没有把三角形的顶点坐标的 w 维度变为 1,而是保留原值,这样,顶点坐标的 w 值其实就是观察空间中的真实的 z 值
而这两句
float zp = alpha * t.v[0].z() / t.v[0].w() + beta * t.v[1].z() / t.v[1].w() + gamma * t.v[2].z() / t.v[2].w();
zp *= Z;
算的是
z p = ( Z 1 ′ Z 2 ′ Z 3 ′ ) ( α β γ ) = ( Z 1 ′ Z 2 ′ Z 3 ′ ) ( Z Z 1 α ′ Z Z 2 β ′ Z Z 3 γ ′ ) = ( Z 1 ′ Z 2 ′ Z 3 ′ ) ( 1 Z 1 α ′ 1 Z 2 β ′ 1 Z 3 γ ′ ) Z zp = \left (\begin{array}{cccc} Z_1' & Z_2' & Z_3' \end{array}\right) \left (\begin{array}{cccc} \alpha \\ \beta \\ \gamma \end{array}\right) \\ = \left (\begin{array}{cccc} Z_1' & Z_2' & Z_3' \end{array}\right) \left (\begin{array}{cccc} \dfrac{Z}{Z_1}\alpha' \\ \dfrac{Z}{Z_2}\beta' \\ \dfrac{Z}{Z_3}\gamma' \end{array}\right) \\ = \left (\begin{array}{cccc} Z_1' & Z_2' & Z_3' \end{array}\right) \left (\begin{array}{cccc} \dfrac{1}{Z_1}\alpha' \\ \dfrac{1}{Z_2}\beta' \\ \dfrac{1}{Z_3}\gamma' \end{array}\right)Z zp=(Z1′Z2′Z3′) αβγ =(Z1′Z2′Z3′) Z1Zα′Z2Zβ′Z3Zγ′ =(Z1′Z2′Z3′) Z11α′Z21β′Z31γ′ Z
其中
float zp = alpha * t.v[0].z() / t.v[0].w() + beta * t.v[1].z() / t.v[1].w() + gamma * t.v[2].z() / t.v[2].w();
算的是
( Z 1 ′ Z 2 ′ Z 3 ′ ) ( 1 Z 1 α ′ 1 Z 2 β ′ 1 Z 3 γ ′ ) \left (\begin{array}{cccc} Z_1' & Z_2' & Z_3' \end{array}\right) \left (\begin{array}{cccc} \dfrac{1}{Z_1}\alpha' \\ \dfrac{1}{Z_2}\beta' \\ \dfrac{1}{Z_3}\gamma' \end{array}\right) (Z1′Z2′Z3′) Z11α′Z21β′Z31γ′
而其他属性之所以不需要透视校正,只是因为三个顶点上的属性不会受到透视投影的影响
比如颜色,UV 坐标
而像是 normal,viewspace_pos 这种,都是在 MV 之后的,也就是都在观察空间中的,也没有经过透视投影
所以目前也就只有深度需要做这个透视校正
第一个任务 rasterize_triangle;实现 normal shader
首先填上作业 2 的写法:
//Screen space rasterization
void rst::rasterizer::rasterize_triangle(const Triangle& t, const std::array<Eigen::Vector3f, 3>& view_pos)
{
// TODO: From your HW3, get the triangle rasterization code.
// TODO: Inside your rasterization loop:
// * v[i].w() is the vertex view space depth value z.
// * Z is interpolated view space depth for the current pixel
// * zp is depth between zNear and zFar, used for z-buffer
// float Z = 1.0 / (alpha / v[0].w() + beta / v[1].w() + gamma / v[2].w());
// float zp = alpha * v[0].z() / v[0].w() + beta * v[1].z() / v[1].w() + gamma * v[2].z() / v[2].w();
// zp *= Z;
// TODO: Interpolate the attributes:
// auto interpolated_color
// auto interpolated_normal
// auto interpolated_texcoords
// auto interpolated_shadingcoords
// Use: fragment_shader_payload payload( interpolated_color, interpolated_normal.normalized(), interpolated_texcoords, texture ? &*texture : nullptr);
// Use: payload.view_pos = interpolated_shadingcoords;
// Use: Instead of passing the triangle's color directly to the frame buffer, pass the color to the shaders first to get the final color;
// Use: auto pixel_color = fragment_shader(payload);
int x_screen_min = width - 1;
int x_screen_max = 0;
int y_screen_min = height - 1;
int y_screen_max = 0;
for (int i = 0; i < 3; i++) {
x_screen_min = std::min(x_screen_min, (int)t.v[i][0]);
y_screen_min = std::min(y_screen_min, (int)t.v[i][1]);
x_screen_max = std::max(x_screen_max, (int)t.v[i][0]);
y_screen_max = std::max(y_screen_max, (int)t.v[i][1]);
}
for (int x = x_screen_min; x <= x_screen_max; ++x) {
for (int y = y_screen_min; y <= y_screen_max; ++y) {
if (insideTriangle(x + 0.5f, y + 0.5f, t.v)) {
auto [alpha, beta, gamma] = computeBarycentric2D(x + 0.5f, y + 0.5f, t.v);
float Z = 1.0 / (alpha / t.v[0].w() + beta / t.v[1].w() + gamma / t.v[2].w());
float zp = alpha * t.v[0].z() / t.v[0].w() + beta * t.v[1].z() / t.v[1].w() + gamma * t.v[2].z() / t.v[2].w();
zp *= Z;
int index = get_index(x, y);
if (depth_buf[index] > zp) {
set_pixel(Vector3f(x, y, zp), t.getColor());
depth_buf[index] = zp;
}
}
}
}
}
这里就没有用之前的 toVector4() 了
然后作业中说我们要实现法向量、颜色、纹理颜色的插值
我之后看那个注释,再看了一下 main 函数里面的,多了一些 shader 的定义,用 C++ 写的 shader……很强
然后 main 里面就是多了一步要设置光栅化器的顶点和片元 shader 而已
那么它定义的片元 shader 是接受一个 fragment_shader_payload 结构体,很强啊很强,这么一说我就能跟一般写的 shader 联系起来了
然后再回到他这个光栅化器的 rasterize_triangle 函数中,它的注释中要求我们先建一个 fragment_shader_payload,传给 shader 再得到 color,很强
所以我觉得大体框架应该是这么写
// temp var
Eigen::Vector3f interpolated_color;
Eigen::Vector3f interpolated_normal;
Eigen::Vector2f interpolated_texcoords;
Eigen::Vector3f interpolated_shadingcoords;
for (int x = x_screen_min; x <= x_screen_max; ++x) {
for (int y = y_screen_min; y <= y_screen_max; ++y) {
if (insideTriangle(x + 0.5f, y + 0.5f, t.v)) {
auto [alpha, beta, gamma] = computeBarycentric2D(x + 0.5f, y + 0.5f, t.v);
float Z = 1.0 / (alpha / t.v[0].w() + beta / t.v[1].w() + gamma / t.v[2].w());
float zp = alpha * t.v[0].z() / t.v[0].w() + beta * t.v[1].z() / t.v[1].w() + gamma * t.v[2].z() / t.v[2].w();
zp *= Z;
int index = get_index(x, y);
if (depth_buf[index] > zp) {
// todo: interpolate
// pass to frag shader
fragment_shader_payload payload(interpolated_color, interpolated_normal.normalized(), interpolated_texcoords, texture ? &*texture : nullptr);
payload.view_pos = interpolated_shadingcoords;
auto pixel_color = fragment_shader(payload);
// update buffer
set_pixel(Vector3f(x, y, zp), pixel_color);
depth_buf[index] = zp;
}
}
}
}
但是我不知道这个 interpolated_shadingcoords 是什么
然后我就不知道这个 payload.view_pos 是什么
于是我就去看 shader 中对这个参数的用法
Eigen::Vector3f phong_fragment_shader(const fragment_shader_payload& payload)
{
Eigen::Vector3f ka = Eigen::Vector3f(0.005, 0.005, 0.005);
Eigen::Vector3f kd = payload.color;
Eigen::Vector3f ks = Eigen::Vector3f(0.7937, 0.7937, 0.7937);
auto l1 = light{{20, 20, 20}, {500, 500, 500}};
auto l2 = light{{-20, 20, 0}, {500, 500, 500}};
std::vector<light> lights = {l1, l2};
Eigen::Vector3f amb_light_intensity{10, 10, 10};
Eigen::Vector3f eye_pos{0, 0, 10};
float p = 150;
Eigen::Vector3f color = payload.color;
Eigen::Vector3f point = payload.view_pos;
Eigen::Vector3f normal = payload.normal;
Eigen::Vector3f result_color = {0, 0, 0};
for (auto& light : lights)
{
// TODO: For each light source in the code, calculate what the *ambient*, *diffuse*, and *specular*
// components are. Then, accumulate that result on the *result_color* object.
}
return result_color * 255.f;
}
我就感觉,灯光的位置有了,人眼的位置有了,剩下的就是着色点的位置了
所以这个 interpolated_shadingcoords 应该是着色点的位置
所以我补充为:
if (depth_buf[index] > zp) {
// todo: interpolate
interpolated_color = interpolate(alpha, beta, gamma, t.color[0], t.color[1], t.color[2], 1.0f);
interpolated_normal = interpolate(alpha, beta, gamma, t.normal[0], t.normal[1], t.normal[2], 1.0f);
interpolated_texcoords = interpolate(alpha, beta, gamma, t.tex_coords[0], t.tex_coords[1], t.tex_coords[2], 1.0f);
interpolated_shadingcoords = interpolate(alpha, beta, gamma, (Eigen::Vector3f)t.v[0].head<3>(), t.v[1].head<3>(), t.v[2].head<3>(), 1.0f);
// pass to frag shader
fragment_shader_payload payload(interpolated_color, interpolated_normal.normalized(), interpolated_texcoords, texture ? &*texture : nullptr);
payload.view_pos = interpolated_shadingcoords;
auto pixel_color = fragment_shader(payload);
// update buffer
set_pixel(Vector3f(x, y, zp), pixel_color);
depth_buf[index] = zp;
}
希望是对的……
实际编译会有错误
C2338: YOU_MIXED_DIFFERENT_NUMERIC_TYPES__YOU_NEED_TO_USE_THE_CAST_METHOD_OF_MATRIXBASE_TO_CAST_NUMERIC_TYPES_EXPLICI
TLY
根据这个报错提示的上面一句话,他正在查看的函数的文件和行数,可以看到是我 set_pixel(Vector3f(x, y, zp), pixel_color); 错了
之后我才看到原来新框架的 set_pixel 改了形参,于是我改成
if (depth_buf[index] > zp) {
// todo: interpolate
interpolated_color = interpolate(alpha, beta, gamma, t.color[0], t.color[1], t.color[2], 1.0f);
interpolated_normal = interpolate(alpha, beta, gamma, t.normal[0], t.normal[1], t.normal[2], 1.0f);
interpolated_texcoords = interpolate(alpha, beta, gamma, t.tex_coords[0], t.tex_coords[1], t.tex_coords[2], 1.0f);
interpolated_shadingcoords = interpolate(alpha, beta, gamma, (Eigen::Vector3f)t.v[0].head<3>(), (Eigen::Vector3f)t.v[1].head<3>(), (Eigen::Vector3f)t.v[2].head<3>(), 1.0f);
// pass to frag shader
fragment_shader_payload payload(interpolated_color, interpolated_normal.normalized(), interpolated_texcoords, texture ? &*texture : nullptr);
payload.view_pos = interpolated_shadingcoords;
auto pixel_color = fragment_shader(payload);
// update buffer
set_pixel(Vector2i(x, y), pixel_color);
depth_buf[index] = zp;
}
cmake 查找不到 opencv
我之前都懒得构建……但是这个作业不是说首先可以构建一下,看看法线贴图的效果嘛
果然我一试就有问题
首先是 cmake 提示我没有 opencv
于是我把我的 opencv 的绝对路径填到 cmakelist 里面了
cmake_minimum_required(VERSION 3.10)
project(Rasterizer)
find_package(OpenCV REQUIRED PATHS D:/Work/opencv/build/x64/vc16/lib)
set(CMAKE_CXX_STANDARD 17)
include_directories(/usr/local/include ./include)
add_executable(Rasterizer main.cpp rasterizer.hpp rasterizer.cpp global.hpp Triangle.hpp Triangle.cpp Texture.hpp Texture.cpp Shader.hpp OBJ_Loader.h)
target_link_libraries(Rasterizer ${OpenCV_LIBRARIES})
#target_compile_options(Rasterizer PUBLIC -Wall -Wextra -pedantic)
make : 无法将“make”项识别为 cmdlet、函数、脚本文件或可运行程序的名称
我的 mingw 确实装好了环境变量
但是他这个 bin 里面的文件默认是 mingw32-make.exe,不叫 make.exe
我就复制了一份,然后把副本重命名为 make.exe
make: *** No targets specified and no makefile found. Stop.
这是因为系统不一样,所以 cmake 的指令的效果不一样
windows 上的 cmake 指令不会生成 makefile
https://www.cnblogs.com/Guang-Jun/p/16911071.html
所以在 Windows 上想要编译的话,应该使用的指令是
mkdir build
cd ./build
cmake ..
cmake --build .
或者
mkdir build
cd ./build
cmake .. -G "Unix Makefiles"
make
can’t open/read file: check file path/integrity
因为我的 exe 构建到了 build 底下的一个 Debug 文件夹下,所以我在 Debug 文件夹中运行的时候,它向上找没找到 model 文件夹
所以我把 exe 和 pdb 文件都移出来了
cv::cvtColor(image_data, image_data, cv::COLOR_RGB2BGR); 报错
我用命令行运行我的 exe 没有显示……于是我回到 VS 中调试
结果会报错
0x00007FF8C7B2FDEC 处(位于 Games101Homework.exe 中)有未经处理的异常: Microsoft C++ 异常: cv::Exception,位于内存位置 0x000000827D6FECB0 处。
[ WARN:0@0.132] global loadsave.cpp:244 cv::findDecoder imread_('../models/spot/hmap.jpg'): can't open/read file: check file path/integrity
具体就是这一块……
但是我就算改成了 './models/spot/hmap.jpg' 也不行……那我就不知道具体是哪错了……
于是最后我用了绝对路径
然后不光是图片,模型的地址我也用的绝对路径,那么现在我 VS 中调试就有效果了
编译出来的 exe 点击执行没有弹出 opencv 窗口
但是即使现在 VS 可以运行了,编译出来的 exe 仍然没有弹出窗口
我放弃了……反正 VS 中能跑就好了
实现 phong_fragment_shader
shader 中的光源
https://games-cn.org/forums/topic/zuoye3wenti/#post-16630
个人感觉 shader 中的光源的位置就是写死了观察空间中的位置
感觉实际中光源的位置也是一个传入的值,或许也是需要经过变换的,但是在这个 shader 里为了简单就写死了
报错 C2338 INVALID_VECTOR_VECTOR_PRODUCT__IF_YOU_WANTED_A_DOT_OR_COEFF_WISE_PRODUCT_YOU_MUST_USE_THE_EXPLICIT_FUNCTIONS
报错 C2338 是因为这句
Eigen::Vector3f ambient = ka * amb_light_intensity;
看上去是因为我不能使用乘号
https://forum.kde.org/viewtopic.php?f=74&t=121249
看了别人的帖子,说是这个报错的意思是不清楚你想要点乘还是按元素相乘
但是我不知道他按元素相乘的函数是什么……官方的示例里面也没有
但是我看他这个报错里面写的函数是 COEFF_WISE_PRODUCT,于是搜了一下,确实发现 cwiseProduct 是点乘
于是正确的写法是
Eigen::Vector3f ambient = ka.cwiseProduct(amb_light_intensity);
做出来黑白的效果
Eigen::Vector3f phong_fragment_shader(const fragment_shader_payload& payload)
{
Eigen::Vector3f ka = Eigen::Vector3f(0.005, 0.005, 0.005);
Eigen::Vector3f kd = payload.color;
Eigen::Vector3f ks = Eigen::Vector3f(0.7937, 0.7937, 0.7937);
auto l1 = light{{20, 20, 20}, {500, 500, 500}};
auto l2 = light{{-20, 20, 0}, {500, 500, 500}};
std::vector<light> lights = {l1, l2};
Eigen::Vector3f amb_light_intensity{10, 10, 10};
Eigen::Vector3f eye_pos{0, 0, 10};
float p = 150;
Eigen::Vector3f color = payload.color;
Eigen::Vector3f point = payload.view_pos;
Eigen::Vector3f normal = payload.normal;
Eigen::Vector3f result_color = {0, 0, 0};
Eigen::Vector3f v = (eye_pos - point).normalized();
for (auto& light : lights)
{
// TODO: For each light source in the code, calculate what the *ambient*, *diffuse*, and *specular*
// components are. Then, accumulate that result on the *result_color* object.
Eigen::Vector3f l = (light.position - point).normalized();
Eigen::Vector3f h = (v + l).normalized();
Eigen::Vector3f ambient = ka.cwiseProduct(amb_light_intensity);
Eigen::Vector3f diffuse = kd.cwiseProduct(light.intensity) / l.squaredNorm() * std::max(0.0f, normal.dot(l));
Eigen::Vector3f specular = ks.cwiseProduct(light.intensity) / l.squaredNorm() * std::powf(std::max(0.0f, normal.dot(h)), p);
result_color += (ambient + diffuse + specular);
}
return result_color * 255.f;
}
这个效果明显是光强算出来很大,那就是有些地方算大了
整个模型变成灰色:着色点的坐标空间搞错了
后面发现是我再算距离的平方的时候用距离的单位向量去算了……然后改成
for (auto& light : lights)
{
// TODO: For each light source in the code, calculate what the *ambient*, *diffuse*, and *specular*
// components are. Then, accumulate that result on the *result_color* object.
Eigen::Vector3f l = (light.position - point).normalized();
Eigen::Vector3f h = (v + l).normalized();
float r2 = (light.position - point).squaredNorm();
Eigen::Vector3f ambient = ka.cwiseProduct(amb_light_intensity);
Eigen::Vector3f diffuse = kd.cwiseProduct(light.intensity) / r2 * std::max(0.0f, normal.dot(l));
Eigen::Vector3f specular = ks.cwiseProduct(light.intensity) / r2 * std::powf(std::max(0.0f, normal.dot(h)), p);
result_color += (ambient + diffuse + specular);
}
之后我对照别人的作业,才发现是我 rasterize_triangle() 这里写错了
原来我写错的是:
interpolated_shadingcoords = interpolate(alpha, beta, gamma, (Eigen::Vector3f)t.v[0].head<3>(), (Eigen::Vector3f)t.v[1].head<3>(), (Eigen::Vector3f)t.v[2].head<3>(), 1.0f);
正确的是:
interpolated_shadingcoords = interpolate(alpha, beta, gamma, view_pos[0], view_pos[1], view_pos[2], 1.0f);
那我之前也是以为三角形对象中的 v 就可以传到片元着色器中
之后发现不是,看 draw() 函数,这里传入到片元着色器中的着色点的坐标是位于 MV 空间中的
而三角形对象中的 v 是 MVP 到 NDC,NDC 到屏幕空间之后的坐标
我在这两个不同的坐标的位置加了中文注释
void rst::rasterizer::draw(std::vector<Triangle *> &TriangleList) {
float f1 = -(50 - 0.1) / 2.0;
float f2 = -(50 + 0.1) / 2.0;
Eigen::Matrix4f mvp = projection * view * model;
for (const auto& t:TriangleList)
{
Triangle newtri = *t;
std::array<Eigen::Vector4f, 3> mm {
(view * model * t->v[0]),
(view * model * t->v[1]),
(view * model * t->v[2])
};
std::array<Eigen::Vector3f, 3> viewspace_pos;
// 在这里获得 MV 之后的三角形顶点坐标
// 三角形的片元着色器中的着色点的坐标是位于 MV 空间中的
std::transform(mm.begin(), mm.end(), viewspace_pos.begin(), [](auto& v) {
return v.template head<3>();
});
Eigen::Vector4f v[] = {
mvp * t->v[0],
mvp * t->v[1],
mvp * t->v[2]
};
//Homogeneous division
for (auto& vec : v) {
vec.x()/=vec.w();
vec.y()/=vec.w();
vec.z()/=vec.w();
}
Eigen::Matrix4f inv_trans = (view * model).inverse().transpose();
Eigen::Vector4f n[] = {
inv_trans * to_vec4(t->normal[0], 0.0f),
inv_trans * to_vec4(t->normal[1], 0.0f),
inv_trans * to_vec4(t->normal[2], 0.0f)
};
//Viewport transformation
for (auto & vert : v)
{
vert.x() = 0.5*width*(vert.x()+1.0);
vert.y() = 0.5*height*(vert.y()+1.0);
vert.z() = vert.z() * f1 + f2;
}
// 在这里把 MVP 到 NDC,NDC 到屏幕空间之后的三角形顶点坐标赋给三角形
for (int i = 0; i < 3; ++i)
{
//screen space coordinates
newtri.setVertex(i, v[i]);
}
for (int i = 0; i < 3; ++i)
{
//view space normal
newtri.setNormal(i, n[i].head<3>());
}
newtri.setColor(0, 148,121.0,92.0);
newtri.setColor(1, 148,121.0,92.0);
newtri.setColor(2, 148,121.0,92.0);
// Also pass view space vertice position
rasterize_triangle(newtri, viewspace_pos);
}
}
那么之后就可以做出来结果了
Eigen::Vector3f phong_fragment_shader(const fragment_shader_payload& payload)
{
Eigen::Vector3f ka = Eigen::Vector3f(0.005, 0.005, 0.005);
Eigen::Vector3f kd = payload.color;
Eigen::Vector3f ks = Eigen::Vector3f(0.7937, 0.7937, 0.7937);
auto l1 = light{{20, 20, 20}, {500, 500, 500}};
auto l2 = light{{-20, 20, 0}, {500, 500, 500}};
std::vector<light> lights = {l1, l2};
Eigen::Vector3f amb_light_intensity{10, 10, 10};
Eigen::Vector3f eye_pos{0, 0, 10};
float p = 150;
Eigen::Vector3f color = payload.color;
Eigen::Vector3f point = payload.view_pos;
Eigen::Vector3f normal = payload.normal.normalized();
Eigen::Vector3f result_color = {0, 0, 0};
Eigen::Vector3f v = (eye_pos - point).normalized();
for (auto& light : lights)
{
// TODO: For each light source in the code, calculate what the *ambient*, *diffuse*, and *specular*
// components are. Then, accumulate that result on the *result_color* object.
Eigen::Vector3f l = (light.position - point).normalized();
Eigen::Vector3f h = (v + l).normalized();
float r2 = (light.position - point).squaredNorm();
Eigen::Vector3f ambient = ka.cwiseProduct(amb_light_intensity);
Eigen::Vector3f diffuse = kd.cwiseProduct(light.intensity) / r2 * std::max(0.0f, normal.dot(l));
Eigen::Vector3f specular = ks.cwiseProduct(light.intensity) / r2 * std::pow(std::max(0.0f, normal.dot(h)), p);
result_color += (ambient + diffuse + specular);
}
return result_color * 255.f;
}
我在排这个 Bug 的时候去看了别人的答案
有一个是没写 Blinn-Phong 而是写了 Phong 模型的
https://blog.csdn.net/weixin_46911332/article/details/121195397
result_color += ks.cwiseProduct (light.intensity / r2) * std:: pow(std::max(0.0f, now_eye.normalized().dot(reflect(light_pos, normal).normalized())), p);
对于我来说就是
Eigen::Vector3f specular = ks.cwiseProduct(light.intensity) / r2 * std::pow(std::max(0.0f, v.dot(reflect(l, normal).normalized())), p);
还有人算半程向量的时候没有用两个方向向量来算的……逆天,估计是复制粘贴别人的吧
它们的代码像这样
//光的方向
Eigen::Vector3f light_dir = light.position - point;
//视线方向
Eigen::Vector3f view_dir = eye_pos - point;
...
//specular镜面反射
//半程向量:视线方向和光线方向平均
Eigen::Vector3f h = (light_dir + view_dir).normalized();
正常的 phong 效果图?
之后我又调出来这样子的
主要是在 debug 的过程中自己也忘了修改了什么地方……?
这个图是我看到别人大部分都是这样的……就很神奇
透视校正重心坐标;法线乘以 MV 逆变换
这个帖子
https://games-cn.org/forums/topic/zuoye3-interpolated_shadingcoords/
也讲了为什么要在 MV 空间中做片元着色,MV 之后的空间,观察空间,是真实光线反射的空间,投影变换之后相当于把这个空间压扁了,所以投影空间中不是真实光线产生作用的空间
还讲了重心坐标应该在三维空间中插值……/
还讲了法线为什么要乘以 MV 的逆变换,是因为原来的 v T ⋅ n = 0 v^T \cdot n = 0 vT⋅n=0
到了投影空间中应该有 v ′ T ⋅ n ′ = 0 v'^T \cdot n' = 0 v′T⋅n′=0,这就要求 v ′ T ⋅ n ′ = v T ⋅ n v'^T \cdot n' = v^T \cdot n v′T⋅n′=vT⋅n
那么既然顶点的变换是 v ′ = V M v v' = VMv v′=VMv,就有 v ′ T = v T ( V M ) T v'^T = v^T (VM)^T v′T=vT(VM)T 为了让 v ′ ⋅ n ′ = v ⋅ n v' \cdot n' = v \cdot n v′⋅n′=v⋅n,就有 v T ( V M ) T ⋅ n ′ = v ⋅ n v^T (VM)^T \cdot n' = v \cdot n vT(VM)T⋅n′=v⋅n,得 ( V M ) T ⋅ n ′ = n (VM)^T \cdot n' = n (VM)T⋅n′=n
环境光只计算一次
其实感觉正常的 shader,在存在多个光源的时候,环境光只计算一次
但是我上网搜的时候也搜到过那种,可以设置为叠加环境光的做法
但是总之先放在这里吧
Eigen::Vector3f phong_fragment_shader(const fragment_shader_payload& payload)
{
Eigen::Vector3f ka = Eigen::Vector3f(0.005, 0.005, 0.005);
Eigen::Vector3f kd = payload.color;
Eigen::Vector3f ks = Eigen::Vector3f(0.7937, 0.7937, 0.7937);
auto l1 = light{{20, 20, 20}, {500, 500, 500}};
auto l2 = light{{-20, 20, 0}, {500, 500, 500}};
std::vector<light> lights = {l1, l2};
Eigen::Vector3f amb_light_intensity{10, 10, 10};
Eigen::Vector3f eye_pos{0, 0, 10};
float p = 150;
Eigen::Vector3f color = payload.color;
Eigen::Vector3f point = payload.view_pos;
Eigen::Vector3f normal = payload.normal.normalized();
Eigen::Vector3f result_color = {0, 0, 0};
// 环境光只计算一次
Eigen::Vector3f ambient = ka.cwiseProduct(amb_light_intensity);
result_color += ambient;
Eigen::Vector3f v = (eye_pos - point).normalized();
for (auto& light : lights)
{
// TODO: For each light source in the code, calculate what the *ambient*, *diffuse*, and *specular*
// components are. Then, accumulate that result on the *result_color* object.
Eigen::Vector3f l = (light.position - point).normalized();
Eigen::Vector3f h = (v + l).normalized();
float r2 = (light.position - point).squaredNorm();
Eigen::Vector3f diffuse = kd.cwiseProduct(light.intensity) / r2 * std::max(0.0f, normal.dot(l));
// Phong reflection model
// Eigen::Vector3f specular = ks.cwiseProduct(light.intensity) / r2 * std::pow(std::max(0.0f, v.dot(reflect(l, normal).normalized())), p);
// Blinn-Phong reflection model
Eigen::Vector3f specular = ks.cwiseProduct(light.intensity) / r2 * std::pow(std::max(0.0f, normal.dot(h)), p);
result_color += (diffuse + specular);
}
return result_color * 255.f;
}
实现 texture_fragment_shader
模型显示出蓝紫色的混乱的颜色
因为我是调试运行的……要改材质贴图
默认的是 hmap.jpg 要改成 spot_texture.png
libpng warning:iCCP:known incorrect sRGB profile
来自:https://blog.csdn.net/Q_pril/article/details/123598746
第二个问题是在运行时出现的,简单来说,问题在于——Libpng-1.6在检查ICC配置文件方面比以前的版本更严格,可以忽略此警告、不影响程序的结果,如果想要解决,需要从PNG图像中删除ICCP块,参考:
https://stackoverflow.com/questions/22745076/libpng-warning-iccp-known-incorrect-srgb-profile
Bump mapping
懒得写了……主要是原理也还没讲,先抄了别人的
Vector3f t(normal.x() * normal.y() / std::sqrt(normal.x() * normal.x() + normal.z() * normal.z()),
std::sqrt(normal.x() * normal.x() + normal.z() * normal.z()),
normal.z() * normal.y() / std::sqrt(normal.x() * normal.x() + normal.z() * normal.z()));
Vector3f b = normal.cross(t);
Matrix3f TBN;
TBN << t.x(), b.x(), normal.x(),
t.y(), b.y(), normal.y(),
t.z(), b.z(), normal.z();
float u = payload.tex_coords.x();
float v = payload.tex_coords.y();
float w = payload.texture->width;
float h = payload.texture->height;
float dU = kh * kn * (payload.texture->getColor(u + 1.0f / w, v).norm() - payload.texture->getColor(u, v).norm());
float dV = kh * kn * (payload.texture->getColor(u, v + 1.0f / h).norm() - payload.texture->getColor(u, v).norm());
Eigen::Vector3f ln{ -dU,-dV,1.0f };
normal = TBN * ln;
这里是吧 RGB 映射到了标量
https://games-cn.org/forums/topic/displacement-shader%E9%AB%98%E5%85%89%E8%AE%A1%E7%AE%97%E7%BB%93%E6%9E%9C%E5%81%8F%E5%B7%AE%E5%A4%A7%E5%8A%A9%E6%95%99%E5%B8%AE%E7%9C%8B%E7%9C%8B/
https://games-cn.org/forums/topic/displacement-%E5%8E%9F%E7%90%86%E9%97%AE%E9%A2%98/
displacement mapping
Eigen::Vector3f displacement_fragment_shader(const fragment_shader_payload& payload)
{
Eigen::Vector3f ka = Eigen::Vector3f(0.005, 0.005, 0.005);
Eigen::Vector3f kd = payload.color;
Eigen::Vector3f ks = Eigen::Vector3f(0.7937, 0.7937, 0.7937);
auto l1 = light{{20, 20, 20}, {500, 500, 500}};
auto l2 = light{{-20, 20, 0}, {500, 500, 500}};
std::vector<light> lights = {l1, l2};
Eigen::Vector3f amb_light_intensity{10, 10, 10};
Eigen::Vector3f eye_pos{0, 0, 10};
float p = 150;
Eigen::Vector3f color = payload.color;
Eigen::Vector3f point = payload.view_pos;
Eigen::Vector3f normal = payload.normal;
float kh = 0.2, kn = 0.1;
// TODO: Implement displacement mapping here
// Let n = normal = (x, y, z)
// Vector t = (x*y/sqrt(x*x+z*z),sqrt(x*x+z*z),z*y/sqrt(x*x+z*z))
// Vector b = n cross product t
// Matrix TBN = [t b n]
// dU = kh * kn * (h(u+1/w,v)-h(u,v))
// dV = kh * kn * (h(u,v+1/h)-h(u,v))
// Vector ln = (-dU, -dV, 1)
// Position p = p + kn * n * h(u,v)
// Normal n = normalize(TBN * ln)
Vector3f t(normal.x() * normal.y() / std::sqrt(normal.x() * normal.x() + normal.z() * normal.z()),
std::sqrt(normal.x() * normal.x() + normal.z() * normal.z()),
normal.z() * normal.y() / std::sqrt(normal.x() * normal.x() + normal.z() * normal.z()));
Vector3f b = normal.cross(t);
Matrix3f TBN;
TBN << t.x(), b.x(), normal.x(),
t.y(), b.y(), normal.y(),
t.z(), b.z(), normal.z();
float u = payload.tex_coords.x();
float v = payload.tex_coords.y();
float w = payload.texture->width;
float h = payload.texture->height;
float dU = kh * kn * (payload.texture->getColor(u + 1.0f / w, v).norm() - payload.texture->getColor(u, v).norm());
float dV = kh * kn * (payload.texture->getColor(u, v + 1.0f / h).norm() - payload.texture->getColor(u, v).norm());
Eigen::Vector3f ln{ -dU,-dV,1.0f };
point += (kn * normal * payload.texture->getColor(u , v).norm());
normal = TBN * ln;
normal = normal.normalized();
Eigen::Vector3f result_color = {0, 0, 0};
Eigen::Vector3f eye_dir = (eye_pos - point).normalized();
// 环境光只计算一次
Eigen::Vector3f ambient = ka.cwiseProduct(amb_light_intensity);
result_color += ambient;
for (auto& light : lights)
{
// TODO: For each light source in the code, calculate what the *ambient*, *diffuse*, and *specular*
// components are. Then, accumulate that result on the *result_color* object.
Eigen::Vector3f light_dir = (light.position - point).normalized();
Eigen::Vector3f halfway = (eye_dir + light_dir).normalized();
float r2 = (light.position - point).squaredNorm();
Eigen::Vector3f diffuse = kd.cwiseProduct(light.intensity) / r2 * std::max(0.0f, normal.dot(light_dir));
// Phong reflection model
// Eigen::Vector3f specular = ks.cwiseProduct(light.intensity) / r2 * std::pow(std::max(0.0f, v.dot(reflect(l, normal).normalized())), p);
// Blinn-Phong reflection model
Eigen::Vector3f specular = ks.cwiseProduct(light.intensity) / r2 * std::pow(std::max(0.0f, normal.dot(halfway)), p);
result_color += (diffuse + specular);
}
return result_color * 255.f;
}
结果:
我不知道为什么我的置换 shader 的高光跟被人的是不一样的
我的高光都在后面,但是我看别人的高光都在前面
我看了一下我的法线结果,跟别人的是差不多的
高光位置不一样:可能是 interpolated_shadingcoords 忘算了
之后才发现是我光栅化器中的 interpolated_shadingcoords 忘算了,尴尬
我之前是写了的,但是可能在记笔记的时候复制粘贴,然后就意外删掉了
调试方法
看到别人讲了单步调试方法……我没试
https://games-cn.org/forums/topic/vscode-%E4%B8%AD%E8%B0%83%E8%AF%95%E6%96%B9%E6%B3%95/
更换模型
Crate 渲染错误
原来的 crate 的 obj 文件是四个点一个面的,但是我们的 obj loader 是三个点一个面的,所以装配的时候出了问题
https://games-cn.org/forums/topic/%E4%BD%9C%E4%B8%9A3%E6%8D%A2%E6%A8%A1%E5%9E%8B-crate%E5%87%BA%E5%A4%A7%E9%97%AE%E9%A2%98/
我还换了那个 cube 的模型……然后感觉效果很差……不管了
双线性插值
一开始我还在想,如果这个点位于某个单元格的不同位置时,取到的四个临近点的方法是不一样的
比如,这个点在某个格子的左下角的时候和右上角的时候,看上去取的四个临近点不一样
待求点在某个格子的左下角 待求点所在格子时四个临近点所在格子中的右上角
待求点在某个格子的右上角 待求点所在格子时四个临近点所在格子中的左下角
这样的
之后我才醒悟……他这个格子……实际上不要看格子,而是看格子中心
因为格子中心是 0.5f 后缀的,所以要先将待求点转换到格子中心的坐标系中(例如 -0.5f),然后再 floor 或者 ceil,然后再转换回世界坐标系(例如 +0.5f)
我看了别人写的
Eigen::Vector3f getColorBilinear(float u, float v)
{
if(u<0) u=0;
if(v<0) v=0;
if(u>1) u=1;
if(v>1) v=1;
auto u_img = u * (width);
auto v_img = (1 - v) * (height);
float u0 = std::max(1.0,floor(u_img-0.5)), u1 = floor(u_img+0.5);
float v0 = std::max(1.0,floor(v_img-0.5)), v1 = floor(v_img+0.5);
float s = (u_img-u0)/(u1-u0);
float t = (v_img-v0)/(v1-v0);
auto color00 = image_data.at<cv::Vec3b>(v0, u0);
auto color01 = image_data.at<cv::Vec3b>(v0, u1);
auto color10 = image_data.at<cv::Vec3b>(v1, u0);
auto color11 = image_data.at<cv::Vec3b>(v1, u1);
auto color0 = color00 + s*(color01-color00);
auto color1 = color10 + s*(color11-color10);
auto color = color0 + t*(color1-color0);
return Eigen::Vector3f(color[0], color[1], color[2]);
}
https://blog.csdn.net/Q_pril/article/details/123598746
Eigen::Vector3f getColorBilinear(float u, float v)
{
if (u < 0) u = 0;
if (u > 1) u = 1;
if (v < 0) v = 0;
if (v > 1) v = 1;
auto u_img = u * width;
auto v_img = (1 - v) * height;
float u_min = std::floor(u_img);
float u_max = std::min((float)width, std::ceil(u_img));
float v_min = std::floor(v_img);
float v_max = std::min((float)height, std::ceil(v_img));
auto Q11 = image_data.at<cv::Vec3b>(v_max, u_min);
auto Q12 = image_data.at<cv::Vec3b>(v_max, u_max);
auto Q21 = image_data.at<cv::Vec3b>(v_min, u_min);
auto Q22 = image_data.at<cv::Vec3b>(v_min, u_max);
float rs = (u_img - u_min) / (u_max - u_min);
float rt = (v_img - v_max) / (v_min - v_max);
auto cBot = (1 - rs) * Q11 + rs * Q12;
auto cTop = (1 - rs) * Q21 + rs * Q22;
auto P = (1 - rt) * cBot + rt * cTop;
return Eigen::Vector3f(P[0], P[1], P[2]);
}
https://www.freesion.com/article/3463875990/
它们好像都没有我这样想
Eigen::Vector3f getColorBilinear(float u, float v)
{
u = std::clamp(u, 0.0f, 1.0f);
v = std::clamp(v, 0.0f, 1.0f);
float u_img = u * width;
float v_img = (1 - v) * height;
float u_min = std::max(0.5f, std::floor(u_img - 0.5f) + 0.5f);
float u_max = std::min(width - 0.5f, std::ceil(u_img - 0.5f) + 0.5f);
float v_min = std::max(0.5f, std::floor(v_img - 0.5f) + 0.5f);
float v_max = std::min(height - 0.5f, std::ceil(v_img - 0.5f) + 0.5f);
auto Q11 = image_data.at<cv::Vec3b>(v_max, u_min);
auto Q12 = image_data.at<cv::Vec3b>(v_max, u_max);
auto Q21 = image_data.at<cv::Vec3b>(v_min, u_min);
auto Q22 = image_data.at<cv::Vec3b>(v_min, u_max);
float rs = (u_img - u_min) / (u_max - u_min);
float rt = (v_img - v_max) / (v_min - v_max);
auto cBot = (1 - rs) * Q11 + rs * Q12;
auto cTop = (1 - rs) * Q21 + rs * Q22;
auto P = (1 - rt) * cBot + rt * cTop;
return Eigen::Vector3f(P[0], P[1], P[2]);
}
没有双线性插值:
双线性插值: