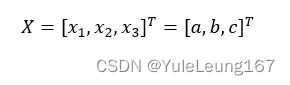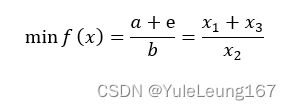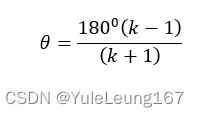MATLAB——最具传力性能的偏置曲柄滑块机构的优化设计（已知H和k）

题目：

已知偏置曲柄滑块机构的行程速比系数K=1.5，滑块行程H=50mm。当原动件曲柄做整周匀速转动时，为了获得良好的传力性能，要求滑块在整个行程中的最小传动角最大，试确定机构的运动结构参数。

数学模型：

设计变量的确定

优化设计中，需要调整和优选的参数称为设计变量。工程上在设计曲柄滑块机构时，一般已知滑块行程H，和行程速比系数K，再通过确定曲柄长度a，连杆长度b，以及偏心距e。因此，在已知道H、K的情况下，以a、b和e为设计变量进行优化设计，其设计变量可以表示为：

建立目标函数

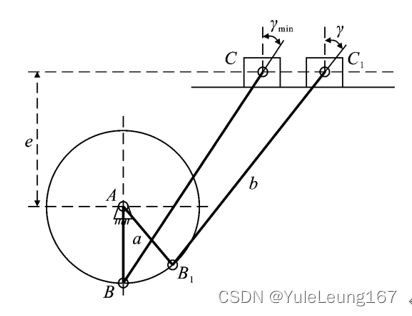
AB为曲柄，BC为连杆，最小传动角γmin出现在图中曲柄与滑块导路垂直的位置。工程上常以γmin的大小衡量机构的传力性能，γmin越大，对传动越有利。以γmin作为目标函数，其计算式为：

在优化设计中，为了使算法与程序一致，一般简化目标函数，简化后的目标函数为：

 

图 机构中γ所在位置

确定约束条件

在实际应用中，对设计变量的取值范围有一定的限制，这种限制在优化设计中被作为数学模型的约束条件。在曲柄滑块机构中，就有曲柄存在的条件a+e≤b，写成不等式约束表达式为：

                             x1-x2+x3≤0                    (4)

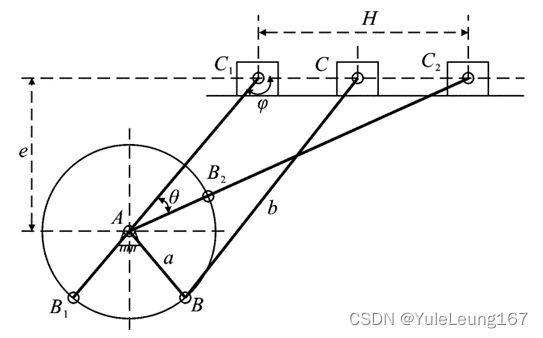
图4为为曲柄滑块的位置关系图。其中C1，C2分别为滑块的左右极限位置，θ为极位夹角，计算公式为：

图 机构左右极限位置

对图 进行运动分析，在三角形AC1C2中，由正弦定理和余弦定理：

可得机构约束等式条件：

结合上述各式：可得曲柄滑块机构的数学模型为：

求解函数

该机构的数学模型是一个同时含有等式约束和不等式约束的优化问题。可用MATLAB优化工具箱中的fmincon求解器进行优化求解，其解决的优化数学模型为：

minfX                                                                       

s.t.              A×X≤b                (线性不等式约束)

                Aeq×X＝beq         (线性等式约束)

                       cX≤0                  (非线性不等式约束)

                  ceqx=0               (非线性等式约束)

       lb≤X≤ub             (X取值范围)

求解程序

编写约束函数

新建funcon.m文件，为非线性约束函数文件。

其中，我这里的H（行程）= 50 ，行程速比k = 1.5

如果不同的结果只要将此处H 和 k 替换就可以了 

function [c,ceq] = funcon(x)

c = [];

H = 50;

k = 1.5;

theta = 180*(k-1)/(k+1);

ceq(1) = (x(2)^2-x(1)^2)*sind(theta)-H*x(3);

ceq(2) = 2*(x(2)^2+x(1)^2)-2*cosd(theta)*(x(2)^2-x(1)^2)-H^2;

end

编写目标函数

新建fun.m文件，为目标函数文件。

function f = fun(x)
f =180/pi*(x(1)+x(3))/x(2);
end

命令行求解代码

在命令行输入以下代码：

A=[1,-1,1];

b=[0];

lb=[0;0;0];

x0=[0,0,0];

[x,fval] = fmincon(@fun,x0,A,b,[],[],lb,[],@funcon)

GammaMin = acos(fval/(180/pi))*180/pi

 运行结果

在MATLAB中运行代码，运行结果为如下：

x =

   22.5370   41.6418   14.4140

fval =

   50.8415

GammaMin =

   27.4576

通过结果可以得知曲柄长a为22.5，连杆长b为41.6，偏心距e为14.4，最小传动角γmin的最大值为27.46°。

 结果分析

创建一个脚本代码

clc
clear
sc=50;
p=62.5392;%计算出来的从曲柄中心到滑块的最远直线距离
e=14.4140;
lambda=22.537/41.6418;%曲柄和连杆的比值
epsilon=e/l;%偏心距和连杆的比值
n=60;%转速
theta=0:10:360;%模拟曲柄转360°
hd=theta.*pi/180;%化为弧度制
W=pi*n/30;%转速
s=r.*(1-cos(hd)-epsilon.*sin(hd)+0.5.*lambda.*sin(hd).^2);%位移
v=r.*W.*(sin(hd)-epsilon.*cos(hd)+0.5.*lambda.*sin(2.*hd));%速度
a=r.*W^2.*(cos(hd)+epsilon.*sin(hd)+lambda.*cos(2.*hd));%加速度

再在命令行输入以下出图代码

figure(1)
subplot(1,3,1);
plot(theta,s,'r')
title('\bf\mus线图')
subplot(1,3,2);
plot(theta,v,'k')
title('\bf\muv线图')
xlabel('\bf曲柄转角\theta(°)')
subplot(1,3,3)
plot(theta,a,'b')
title('\bf\mua线图')

得出运动情况的数值图

 可以看出当曲柄做匀速转动时，由μs位移曲线可得出滑块做往复运动，行程大致为50mm，曲线的最大值和最小值分别对应滑块的左极限和右极限位移。分析μv图当滑块速度为０时，对应位移曲线的最大值和最小值，符合滑块的运动趋势。当滑块位移值最大时，对应μa加速度曲线的最小值，即加速度反向的最大值。而且从μs图可以看出滑块速度曲线上升阶段斜率小于下降阶段斜率，这反映出曲柄滑块机构的急回特性。