Leetcode打卡——二叉搜索树(共8题)
二叉搜索树(BST)是二叉树的一种特殊表示形式,它满足如下特性:
每个节点中的值必须大于(或等于)存储在其左侧子树中的任何值。
每个节点中的值必须小于(或等于)存储在其右子树中的任何值。

1.Leetcode98. 验证二叉搜索树

法一:利用二叉树的性质,根结点的值大于左子树上的点,小于右子树上的点
const long long MAX=2e31;
const long long MIN=-MAX;
class Solution {
public:
bool isValidBST(TreeNode* root) {
bool ans=search(root,MIN,MAX);
return ans;
}
bool search(TreeNode *root,long long l,long long r){
if(root==NULL)return true;
if(root->val<=l||root->val>=r){
return false;
}
return search(root->left,l,root->val)&&search(root->right,root->val,r);
}
};
法二:二叉搜索树中序遍历的结果一定是单调递增的
class Solution {
public:
bool isValidBST(TreeNode* root) {
stack<TreeNode*>st;
TreeNode *cur=root;
long long num=-2*1e10;
while(cur||!st.empty()){
while(cur){
st.push(cur);
cur=cur->left;
}
cur=st.top();
st.pop();
if(num>=cur->val){
return false;
}
num=cur->val;
cur=cur->right;
}
return true;
}
};
2.Leetcode173. 二叉搜索树迭代器
class BSTIterator {
public:
TreeNode *cur;
stack<TreeNode*>st;
BSTIterator(TreeNode* root) {
cur=root;
}
int next() {
while(cur){
st.push(cur);
cur=cur->left;
}
cur=st.top();
st.pop();
int ans=cur->val;
cur=cur->right;
return ans;
}
bool hasNext() {
return cur||!st.empty();
}
};
3.Leetcode700. 二叉搜索树中的搜索
class Solution {
public:
TreeNode *ans=NULL;
TreeNode* searchBST(TreeNode* root, int val) {
if(root==NULL)return root;
if(root->val==val)return root;
if(root->val>val)ans=searchBST(root->left,val);
if(root->val<val)ans=searchBST(root->right,val);
return ans;
}
};
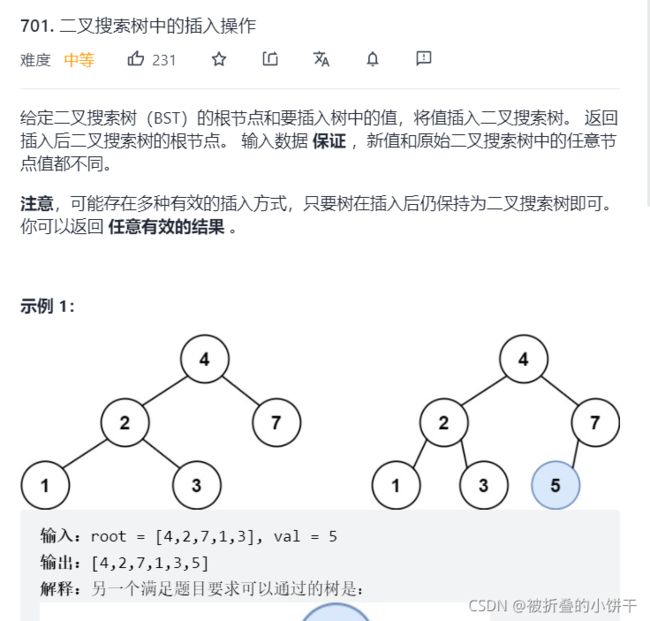
4.Leetcode701. 二叉搜索树中的插入操作
class Solution {
public:
TreeNode* insertIntoBST(TreeNode* root, int val) {
if(root==NULL){
root=new TreeNode(val);
return root;
}
if(root->val>val)root->left=insertIntoBST(root->left,val);
if(root->val<val)root->right=insertIntoBST(root->right,val);
return root;
}
};
5.Leetcode450. 删除二叉搜索树中的节点
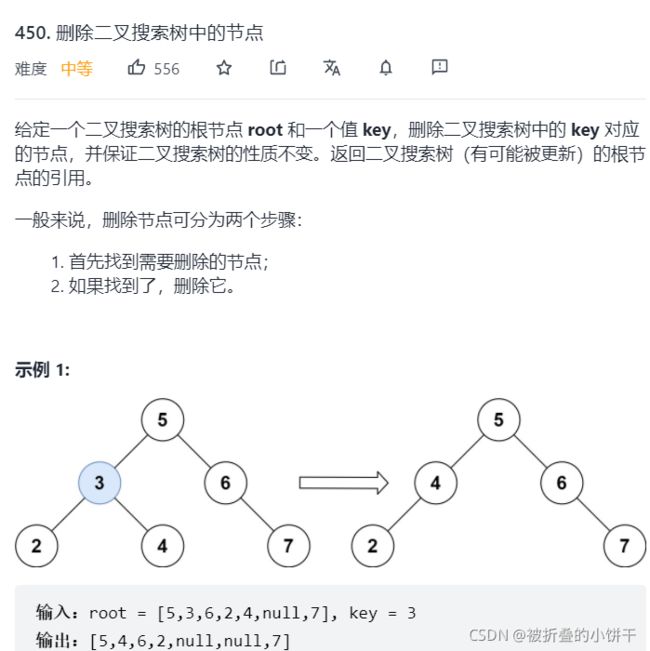
有许多不同的删除节点的方法,为了使整体操作变化最小,用一个合适的子节点来替换要删除的目标节点。根据其子节点的个数,我们需考虑以下三种情况:
- 如果目标节点没有子节点,我们可以直接移除该目标节点。
- 如果目标节只有一个子节点,我们可以用其子节点作为替换。
- 如果目标节点有两个子节点,我们需要用其中序 后继节点或者前驱节点来替换,再删除该目标节点。
要删除的节点不是叶子节点且拥有右节点,则该节点可以由该节点的后继节点进行替代,该后继节点位于右子树中较低的位置。然后可以从后继节点的位置递归向下操作以删除后继节点。
要删除的节点不是叶子节点,且没有右节点但是有左节点。这意味着它的后继节点在它的上面,但是我们并不想返回。我们可以使用它的前驱节点进行替代,然后再递归的向下删除前驱节点。

Successor 代表的是中序遍历序列的下一个节点。即比当前节点大的最小节点,简称后继节点。 先取当前节点的右节点,然后一直取该节点的左节点,直到左节点为空,则最后指向的节点为后继节点。
TreeNode * successor(TreeNode *root){
root=root->right;
while(root->left){
root=root->left;
}
return root;
}
Predecessor 代表的是中序遍历序列的前一个节点。即比当前节点小的最大节点,简称前驱节点。先取当前节点的左节点,然后取该节点的右节点,直到右节点为空,则最后指向的节点为前驱节点。
TreeNode *predecessor(TreeNode *root){
root=root->left;
while(root->right){
root=root->right;
}
return root;
}
class Solution {
public:
TreeNode* deleteNode(TreeNode* root, int key){
if(root==NULL)return NULL;
if(root->val==key){
if(!root->left&&!root->right){
return NULL;
}else if(root->right){
TreeNode *node=new TreeNode(successor(root)->val);
node->left=root->left;
node->right=root->right;
node->right=deleteNode(node->right,node->val);
return node;
}else if(!root->right&&root->left){
TreeNode *node=new TreeNode(precessor(root)->val);
node->left=root->left;
node->right=root->right;
node->left=deleteNode(node->left,node->val);
return node;
}
}
TreeNode *l=deleteNode(root->left,key);
TreeNode *r=deleteNode(root->right,key);
root->left=l;
root->right=r;
return root;
}
TreeNode *successor(TreeNode *root){
root=root->right;
while(root->left){
root=root->left;
}
return root;
}
TreeNode *precessor(TreeNode*root){
root=root->left;
while(root->right){
root=root->right;
}
return root;
}
};
二叉搜索树的有优点是,即便在最坏的情况下,也允许你在O(h)的时间复杂度内执行所有的搜索、插入、删除操作。
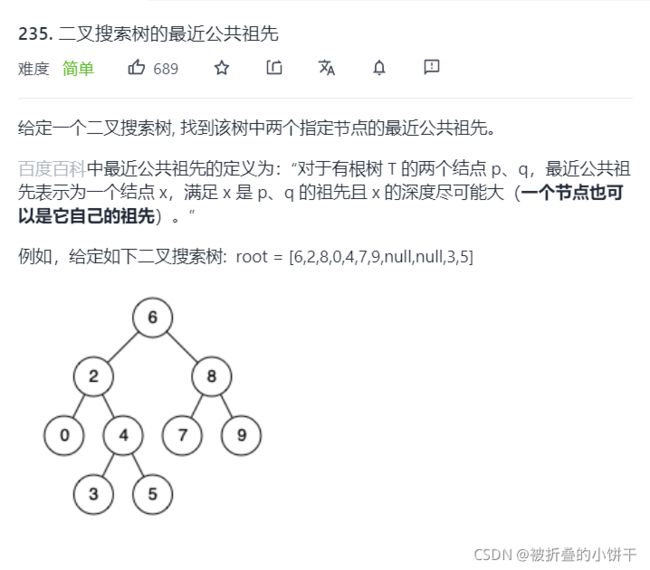
6.Leetcode235. 二叉搜索树的最近公共祖先
class Solution {
public:
TreeNode *ans;
TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
if(root==NULL)return NULL;
search(root,p,q);
return ans;
}
bool search(TreeNode *root,TreeNode*p,TreeNode *q){
if(root==NULL)return false;
bool pr=search(root->left,p,q);
bool qr=search(root->right,p,q);
if(pr&&qr||(root==p||root==q)&&(pr||qr)){
ans=root;
return true;
}
return root==q||root==p||qr||pr;
}
};
法二:
利用二叉搜索树的性质,我们可以快速地找出树中的某个节点以及从根节点到该节点的路径
如果当前节点的值大于 p 和 q 的值,说明 p 和 q 应该在当前节点的左子树,因此将当前节点移动到它的左子节点;
如果当前节点的值小于 p 和 q 的值,说明 p 和 q 应该在当前节点的右子树,因此将当前节点移动到它的右子节点;
如果当前节点的值不满足上述两条要求,那么说明当前节点就是分岔点。此时,p 和 q 要么在当前节点的不同的子树中,要么其中一个就是当前节点。
class Solution {
public:
TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
if(root==NULL)return NULL;
TreeNode *ans=root;
while(ans){
if(ans->val>p->val&&ans->val>q->val){
ans=ans->left;
}else if(ans->val<p->val&&ans->val<q->val){
ans=ans->right;
}else{
break;
}
}
return ans;
}
};
高度平衡的二叉搜索树
一个高度平衡的二叉搜索树(平衡二叉搜索树)是在插入和删除任何节点之后,可以自动保持其高度最小。也就是说,有 N 个节点的平衡二叉搜索树,它的高度是 logN 。并且,每个节点的两个子树的高度不会相差超过 1。
二叉树及其相关操作, 包括搜索、插入、删除。当分析这些操作的时间复杂度时,我们需要注意的是树的高度是十分重要的考量因素。以搜索操作为例,如果二叉搜索树的高度为 h ,则时间复杂度为 O(h) 。二叉搜索树的高度的确很重要。
所以,我们来讨论一下树的节点总数 N 和高度 h 之间的关系。对于一个平衡二叉搜索树, 我们已经在前文中提过,
但一个普通的二叉搜索树,在最坏的情况下,它可以退化成一个链。
因此,具有 N 个节点的二叉搜索树的高度在 logN 到 N 区间变化。也就是说,搜索操作的时间复杂度可以从 logN 变化到 N 。这是一个巨大的性能差异。
所以说,高度平衡的二叉搜索树对提高性能起着重要作用。
高度平衡的二叉搜索树在实际中被广泛使用,因为它可以在 O(logN) 时间复杂度内执行所有搜索、插入和删除操作。
常见的的高度平衡二叉树:
红黑树
AVL树
伸展树
树堆
平衡二叉搜索树的概念经常运用在 Set 和 Map 中。Set 和 Map 的原理相似。
通常,有两种最广泛使用的集合**:散列集合(Hash Set)和 树集合(Tree Set)**。
树集合,Java 中的 Treeset 或者 C++ 中的 set ,是由高度平衡的二叉搜索树实现的。因此,搜索、插入和删除的时间复杂度都是 O(logN) 。
散列集合,Java 中的 HashSet 或者 C++ 中的 unordered_set ,是由哈希实现的,但是平衡二叉搜索树也起到了至关重要的作用。当存在具有相同哈希键的元素过多时,将花费 O(N) 时间复杂度来查找特定元素,其中N是具有相同哈希键的元素的数量。 通常情况下,使用高度平衡的二叉搜索树将把时间复杂度从 O(N) 改善到 O(logN) 。
哈希集和树集之间的本质区别在于树集中的键是有序的。
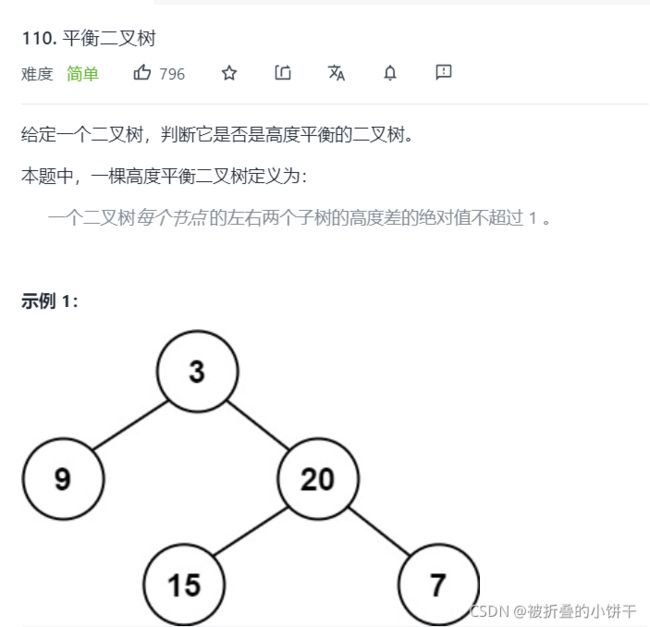
7.110. 平衡二叉树
class Solution {
public:
bool ans=true;
bool isBalanced(TreeNode* root) {
if(root==NULL)return ans;
search(root);
return ans;
}
int search(TreeNode *root){
if(root==NULL)return 0;
int l=search(root->left);
int r=search(root->right);
if(abs(l-r)>1){
ans=false;
return -1;
}
return l>r?l+1:r+1;
}
};
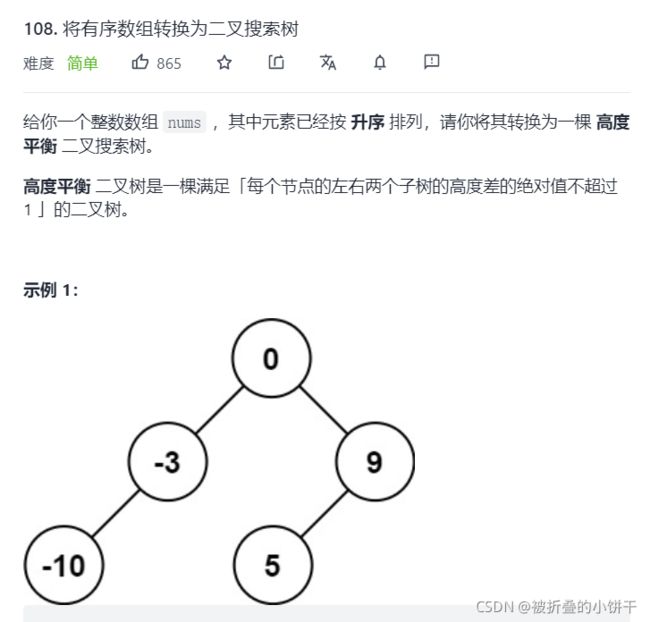
8.Leetcode108. 将有序数组转换为二叉搜索树
class Solution {
public:
TreeNode* sortedArrayToBST(vector<int>& nums) {
return helper(nums, 0, nums.size() - 1);
}
TreeNode* helper(vector<int>& nums, int left, int right) {
if (left > right) {
return nullptr;
}
// 总是选择中间位置左边的数字作为根节点
int mid = (left + right) / 2;
TreeNode* root = new TreeNode(nums[mid]);
root->left = helper(nums, left, mid - 1);
root->right = helper(nums, mid + 1, right);
return root;
}
};