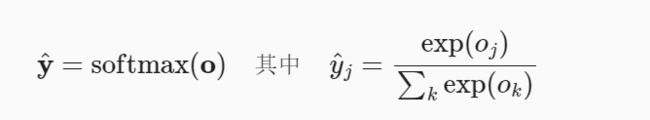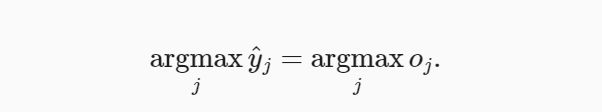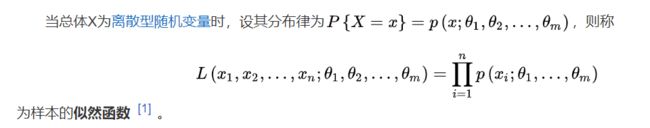动手学深度学习——softmax回归（原理解释+代码详解）

1. softmax回归

回归是问“多少”，可以用来预测多少，如预测房屋价格。

分类是问“哪一个”，如某个电子邮件是否是垃圾邮件，某个图像描绘的是猫还是狗。

这里引入“硬性”类别和“软性”类别的概念：

• “硬性”类别：属于哪个类别
• “软性”类别：属于每个类别的概率

我们关心硬类别，但仍然使用软类别的模型。

softmax：最大概率的标签，能够将未规范化的预测变换为非负数，并且总和为1，同时能够让模型保持可导。

1.1 分类问题

从一个图像分类问题开始，假设每次输入是一个2×2的灰度图像。我们可以用一个标量表示每个像素值，每个图像对应4个特征x1，x2，x3，x4。此外，假设每个图像属于类别“猫”“鸡”和“狗”中的一个。

接下来，我们要选择如何表示标签。我们有两个明显的选择：

1. 选择y∈{1，2，3}，其中整数分别代表{狗，猫，鸡}。
2. 标签y将是一个三维向量，其中(1,0,0)对应于“狗”，(0,1,0)对应于“鸡”，(0,0,1)对应于“狗”：
   

方法2是一种表示分类数据的简单方法：独热编码（one-hot encoding）。独热编码是一个向量，它的分量和类别一样多，类别对应的分量设置为1，其他所有分量设置为0。

1.2 网络架构

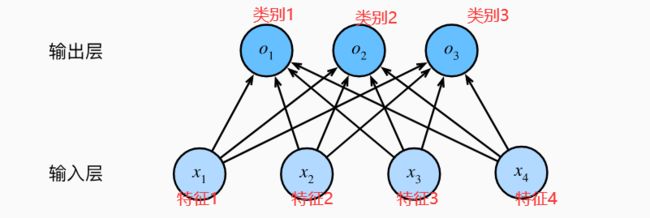
为了估计所有可能类别的条件概率，我们需要一个有多个输出的模型，每个类别对应一个输出。

在上述例子（猫，鸡，狗）中，由于有4个特征和3个可能的输出类别，我们将需要12个标量来表示权重（带下标的w），3个标量来表示偏置（带下标的b）。下面是为每个输入计算三个未规范化的预测（logit）：o1、o2和o3。

用神经网络来描述这个计算过程，与线性回归一样，softmax回归也是一个单层神经网络。由于计算每个输出o1、o2和o3取决于所有输入x1，x2，x3和x4，所以softmax回归的输出层也是全连接层。

1.3 全连接层的参数开销

全连接层是“完全”连接的，对于任何具有d个输入和q个输出的全连接层，参数开销为O(dq)。
若将d个输入转换为q个输出的成本可以减少到O(dq/n)，其中超参数n可以由我们灵活指定。

1.4 softmax运算

我们将优化参数以最大化观测数据的概率，为了得到预测结果，我们将设置一个阈值，如选择最大概率的标签。

我们希望模型输出y(j)可以视为属于类j的概率，然后选择具有最大输出值的类别argmaxy(j)作为我们的预测。例如：y1、y2和y3分别为0.1、0.8和0.1，那我们预测的类别为2，在我们的例子中代表“鸡”。

但我们不能将未规范化的预测o直接作为输出，因为将线性层的输出直接视为概率时会存在一些问题：

• 我们没有限制这些数字的总和为1
• 根据输入的不同，它们可以为负值

要将输出视为概率，我们必须保证在任何数据上的输出都是非负的且总和为1。
此外，我们需要一个训练的目标函数，来激励模型精准地估计概率。例如。在分类器输出0.5的所有样本中，我们希望这些样本是刚好有一半实际上属于预测的类别。 这个属性叫做校准（calibration）。

引入softmax函数： softmax函数能够将未规范化的预测变换为非负数并且总和为1，同时让模型保持可导的性质。

1. 首先，对每个未规范化的预测求冥，这样可以确保输出为非负。
2. 再让每个求冥后的结果除以它们的总和，为了确保最终输出的概率值总和为1。

这里，对于所有的j总有0≤y(j)≤1。因此，y可以视为一个正确的概率分布，softmax不会改变未规范化的预测o之间的大小次序，只会确定分配给每个类别的概率。因此，在预测过程中，我们仍然可以用下式来选择最有可能得类别。
尽管softmax是一个非线性函数，但softmax回归的输出仍然由输入特征的仿射变换决定。因此，softmax回归是一个线性模型。

1.5 小批量样本的矢量化

为了提高计算效率并且充分利用GPU，我们通常会对小批量样本的数据执行矢量计算。

假设我们读取了一个批量的样本X，其中特征维度（输入数量）为d，批量大小为n。此外，假设我们在输出中有q个类别。那么小批量样本各参数的矢量为：

参数	矢量
特征
权重
偏置

softmax回归的矢量计算表达式为：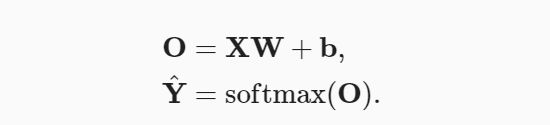
相对于一次处理一个样本， 小批量样本的矢量化加快了X和W的矩阵-向量乘法。 由于X中的每一行代表一个数据样本， 那么softmax运算可以按行（rowwise）执行：对于O的每一行，我们先对所有项进行幂运算，然后通过求和对它们进行标准化。

1.6 损失函数

接下来，我们需要一个损失函数来度量预测的效果。

1.6.1 对数似然

似然函数在概率论中常见，可以用于求条件极值，在这里我们的损失函数的值则要尽量小。

softmax函数给出了一个向量y， 我们可以将其视为“对给定任意输入x的每个类的条件概率”。例如，y=P(y = 猫|x)。假设整个数据集{X,Y}具有n个样本，其中索引i的样本由特征向量x和独热标签向量y组成。我们可以将估计值与实际值进行比较：

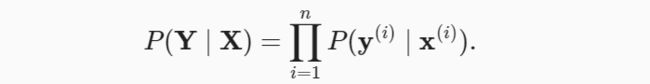
根据最大似然估计，我们最大化P(Y|X)，相当于最小化负对数似然：

由于y是独热编码（形如(1,0,0)），所以除了一个项以外其他项都消失了。所有的y是预测的概率，则对数不会大于0。
如果正确地预测实际标签（即P(y|x)=1），损失函数就不会进一步优化，但这往往不可能。由于存在标签噪声（比如某些样本可能被误标），或输入特征没有足够的信息来完美地对每一个样本分类。

似然函数
极大似然估计

1.6.2 softmax及其导数

利用softmax的定义，我们得到：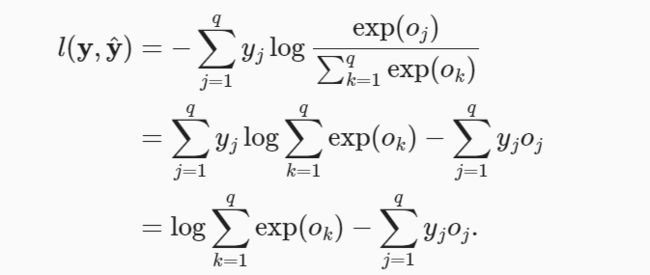
考虑相对于任何未规范化的预测o的导数，我们得到：

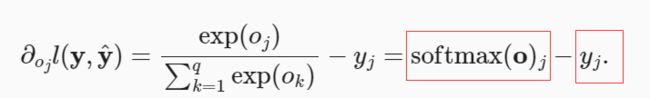
导数是softmax模型分配的概率与实际发生的情况（由独热标签向量表示）之间的差异。

1.6.3 交叉熵损失

对于标签y，我们可以使用与以前相同的表示形式。 唯一的区别是，我们现在用一个概率向量表示，如(0.1,0.2,0.7)，而不是包含二元项的向量(0,0,1)。

对于任何标签y和模型预测y^，损失函数为（通常被称为交叉熵函数，它是所有标签分布的预期损失值）：

1.7 信息论基础

信息论（information theory）涉及编码、解码、发送以及尽可能简洁地处理信息或数据。

1.7.1 熵

通常，一个信源发送出什么符号是不确定的，衡量它可以根据其出现的概率来度量。概率大，出现机会多，不确定性小；反之不确定性就大。

1.7.2 信息量

香农（C. E. Shannon）信息论应用概率来描述不确定性。信息是用不确定性的量度定义的。一个消息的可能性愈小，其信息愈多；而消息的可能性愈大，则其信息愈少。事件出现的概率小，不确定性越多，信息量就大，反之则少。

如果我们不能完全预测每一个事件，那么我们有时可能会感到”惊异”。 克劳德·香农决定用信息量:

来量化这种惊异程度。 在观察一个事件j时，并赋予它（主观）概率P(j)。 当我们赋予一个事件较低的概率时，我们的惊异会更大，该事件的信息量也就更大。

1.7.3 重新审视交叉熵

交叉熵从P到Q，记为H(P,Q)。我们可以把交叉熵想象为“主观概率为Q的观察者在看到根据概率P生成的数据时的预期惊异”。
当P=Q时，交叉熵达到最低。 在这种情况下，从P到Q的交叉熵是H(P,P)=H(P )。

我们从两方面考虑交叉熵分类目标：

1. 最大化观测数据的似然
2. 最小化传达标签所需的惊异

1.8 模型预测与评估

在训练softmax回归模型后，给出任何样本特征，我们可以预测每个输出类别的概率。 通常我们使用预测概率最高的类别作为输出类别。 如果预测与实际类别（标签）一致，则预测是正确的。

1.9 小结

• softmax运算获取一个向量并将其映射为概率。
• softmax回归适用于分类问题，它使用了softmax运算中输出类别的概率分布。
• 交叉熵是一个衡量两个概率分布之间差异的很好的度量，它测量给定模型编码数据所需的比特数。

2. 图像分类数据集

这里采用Fashion-MNIST数据集

• torchvision：torch类型的可视化包，一般计算机视觉和数据可视化需要使用
• from torchvision import transforms：该组件经常用于图片的修改（一般数据集中的图片都是PIL格式，使用的时候需要转化为tenser，而在加入函数时常需要转化为nadarry（numpy中的ndarray为多维数组））
• d2l.use_svg_display()：使用什么模式展示图片

%matplotlib inline
import torch
import torchvision #pytorch用于计算机视觉的一个库
from torch.utils import data
from torchvision import transforms #导入对数据操作的模具
from d2l import torch as d2l

d2l.use_svg_display() #使用svg展示图片

2.1 读取数据集

通过框架中的内置函数将Fashion-MNIST数据集下载并读取到内存中

• torchvision.datasets：一般用于图像数据集的下载和获取
  eg：
• torchvision.datasets.FashionMNIST( root=, train=True, transform=, download=True)：
  • train：是否为训练集
  • transform：使用什么格式转换（可以从transforms组件中选择）
  • dowload：是否下载对应数据集
  • .FashionMNIST可以更换为其他数据源

# 通过ToTensor实例将图像数据从PIL类型变换成32位浮点数格式，
# 并除以255使得所有像素的数值均在0～1之间
trans = transforms.ToTensor() #对图片进行预处理，转换为tensor格式

# 下载训练集和测试集，并保存
mnist_train = torchvision.datasets.FashionMNIST(
	root="../data", train=True, transform=trans,download=True)
mnist_train = torchvision.datasets.FashionMNIST(
	root="../data", train=False, transform=trans,download=True)

Fashion-MNIST由10个类别的图像组成， 每个类别由训练数据集（train dataset）中的6000张图像 和测试数据集（test dataset）中的1000张图像组成。 因此，训练集和测试集分别包含60000和10000张图像。 测试数据集不会用于训练，只用于评估模型性能。

# 输出训练集和测试集的大小
len(mnist_train), len(mnist_test)

每个输入图像的高度和宽度均为28像素。 数据集由灰度图像组成，其通道数为1（彩色图像通道数为3）。

# 索引到第一张图片
mnist_train[0][0].shape # 输入图像的通道数、高度和宽度

Fashion-MNIST中包含的10个类别，分别为t-shirt（T恤）、trouser（裤子）、pullover（套衫）、dress（连衣裙）、coat（外套）、sandal（凉鞋）、shirt（衬衫）、sneaker（运动鞋）、bag（包）和ankle boot（短靴）。以下函数用于在数字标签索引及其文本名称之间进行转换。

# 获取数据集的标签
def get_fashion_mnist_labels(labels): #@save
	"""返回Fashion-MNIST数据集的文本标签"""
	text_labels = ['t-shirt', 'trouser', 'pullover', 'dress', 'coat',
                   'sandal', 'shirt', 'sneaker', 'bag', 'ankle boot']
    return [text_lables[int(i)] for i in labels]

创建一个函数来可视化这些样本。

• plt.subplots()是一个返回包含图形和轴对象的元组的函数。因此，在使用时fig, ax = plt.subplots(),将此元组解压缩到变量fig和ax。
• enumerate()函数用于将一个可遍历的数据对象(如列表、元组或字符串)组合为一个索引序列，同时列出数据和数据下标，一般用在 for 循环当中，生成可以遍历的每个元素有对应序号(0, 1, 2, 3…)的enumerate对象。
• zip()函数用于将多个可迭代对象作为参数，依次将对象中对应的元素打包成一个个元组，然后返回由这些元组组成的对象，里面的每个元素大概为i,(ax,img)的形式。
• imshow()可以接收二维，三维甚至多维数组。二维默认为一通道即灰度图像，三维需要在第三个维度指定图像通道数（必须是第三维）

def show_images(imgs, num_rows, num_cols, titles=None, scale=1.5): #@save
	"""绘制图像列表"""
	figsize = (num_cols * scale, num_rows * scale)
	
	# 第1个参数是个图，一般不用；第2个axer类似于图片的索引矩阵（行，列）
	_, axes = d2l.plt.subplots(num_rows, num_cols, figsize=figsize) # axes：轴
	axes = axes.flatten()

	# 遍历生成形如i, (ax, img)形式的enumerate对象
	for i, (ax, img) in enumerate(zip(axes, imgs)):
		if torch.is_tensor(img):
			# 图片张量
			ax.imshow(img.numpy())
			
		else:
			# PIL图片
			ax.imshow(img)
		ax.axes.get_xaxis().set_visible(False) #x轴隐藏
		ax.axes.get_yaxis().set_visible(False) #y轴隐藏
		if titles:
			ax.set_title(title[i]) #显示标题
	return axes

以下是训练数据集中前几个样本的图像及其相应的标签。

• next() 返回迭代器的下一个项目。
• next() 函数要和生成迭代器的iter() 函数一起使用。
• 我们可以通过iter()函数获取这些可迭代对象的迭代器。然后，我们可以对获取到的迭代器不断使⽤next()函数来获取下⼀条数据。
  注：当我们已经迭代完最后⼀个数据之后，再次调⽤next()函数会抛出 StopIteration的异常 ，来告诉我们所有数据都已迭代完成，不⽤再执⾏ next()函数了。

# 使用next()函数获取批量大小为18的训练集的图像和标签
X, y = next(iter(data.DataLoader(mnist_train, batch_size=18)))

#显示18张图片，宽度为28，长度为28，总共为2行9列
# 绘制两行图片，每一行有9张图片，并获取标签
show_images(X.reshape(18, 28, 28), 2, 9, titles=get_fashion_mnist_labels(y)); 

2.2 读取小批量

为了使我们在读取训练集和测试集时更容易，我们使用内置的数据迭代器，而不是从零开始创建。 回顾一下，在每次迭代中，数据加载器每次都会读取一小批量数据，大小为batch_size。 通过内置数据迭代器，我们可以随机打乱了所有样本，从而无偏见地读取小批量。

batch_size = 256

def get_dataloader_workers(): #@save
	"""使用4个进程来读取数据"""
	return 4

# 训练集需要设置shuffle=True打乱顺序	
train_iter = data.DataLoader(mnist_train, batch_size, shuffle=True,
							 num_workers=get_dataloader_workers())

我们看一下读取训练数据所需的时间。

timer = d2l.Timer() #调用Timer函数，测试速度
for X, y in train_iter:
	continue
f'{timer.stop():.2f} sec' #输出读取数据所用的秒数，精度为2位小数

2.3 整合所有组件

定义load_data_fashion_mnist函数，用于获取和读取Fashion-MNIST数据集。这个函数返回训练集和验证集的数据迭代器。 此外，这个函数还接受一个可选参数resize，用来将图像大小调整为另一种形状。

• torchvision.transforms是pytorch中的图像预处理包，一般用Compose把多个步骤整合到一起。
• insert函数是一种用于列表的内置函数。这个函数的作用是在一个列表中的指定位置，插入一个元素。

transforms中的函数	功能
Resize	把给定的图片resize到given size
Normalize	用均值和标准差归一化张量图像

def load_data_fashion_mnist(batch_size, resize=None):  #@save
	"""下载Fashion-MNIST数据集，然后将其加载到内存中"""
	# 转换为tensor
	trans = [transforms.ToTensor()]

	
	if resize:
		trans.insert(0, transforms.Resize(resize))
	# compose整合步骤
	trans = transforms.Compose(trans)

	# 下载训练集和测试集，并返回到train_iter中，用于之后的训练
	mnist_train = torchvision.datasets.FashionMNIST(
		root="../data", train=True, transform=trans, download=True)
	mnist_test = torchvision.datasets.FashionMNIST(
		root="../data", train=False, transform=trans, download=True)
	return (data.DataLoader(mnist_train, batch_size, shuffle=True,
							num_workers=get_dataloader_workers()),
			data.DataLoader(mnist_test, batch_size, shuffle=False,
							num_workers=get_dataloader_workers()))

下面，我们通过指定resize参数来测试load_data_fashion_mnist函数的图像大小调整功能。

train_iter, test_iter = load_data_fashion_mnist(32, resize=64)
for X, y in train_iter:
	print(X.shape, X.dtype, y.shape, y.dtype)
	break

2.4 小结

• Fashion-MNIST是一个服装分类数据集，由10个类别的图像组成。我们将在后续章节中使用此数据集来评估各种分类算法。
• 我们将高度h像素，宽度w像素图像的形状记为h×w或(h,w)。
• 数据迭代器是获得更高性能的关键组件。依靠实现良好的数据迭代器，利用高性能计算来避免减慢训练过程。

3. softmax回归的从零开始实现

引入Fashion-MNIST数据集， 并设置数据迭代器的批量大小为256。

import torch
from IPython import display
from d2l import torch as d2l

# 随机读取256张图片
batch_size = 256

# 返回训练集和测试集的迭代器
# load_data_fashion_mnist函数是在图像分类数据集中定义的一个函数，可以返回batch_size大小的训练数据集和测试数据集
train_iter, test_iter = d2l.load_data_fashion_mnist(batch_size)

步骤	函数
载入数据集
初始化模型参数
定义softmax操作
定义模型
定义损失函数
分类精度
训练
预测

3.1 初始化模型参数

1. 样本固定长度向量表示，原始数据集每个样本都是28×28的图像
2. 现在将展平每个图像，把它们看作长度为784的向量
3. 在softmax回归中，我们的输出与类别一样多。 因为我们的数据集有10个类别，所以网络输出维度为10
4. 权重将构成一个784×10的矩阵， 偏置将构成一个1×10的行向量

num_inputs = 784 #展平长度为784的向量
num_outputs = 10 #10输出，也对应10类别

# 权重w：均值为0，标准差为0.01，数量size为输入输出的数量
# size=(num_inputs, num_outputs)：行数为输入的个数，列数等于输出的个数
# requires_grad=True表明要计算梯度
W = torch.normal(0, 0.01, size=(num_inputs, num_outputs), requires_grad=True)
b = torch.zeros(num_outputs, requires_grad=True)

3.2 定义softmax操作

sum运算符：给定一个矩阵X，我们可以对所有元素求和（默认情况下）。 也可以只求同一个轴上的元素，即同一列（轴0）或同一行（轴1）。

一般实现softmax由三个步骤组成：

1. 对每个项求幂（使用exp）；
2. 对每一行求和（小批量中每个样本是一行），得到每个样本的规范化常数；
3. 将每一行除以其规范化常数，确保结果的和为1。

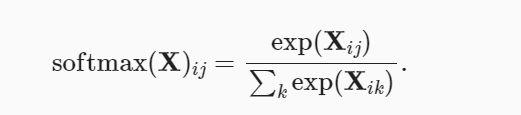
# 定义softmax函数
def softmax(X):
    X_exp = torch.exp(X) # 对每个元素做指数运算
    partition = X_exp.sum(1, keepdim=True) # 对每行进行求和
    return X_exp / partition  # 这里应用了广播机制

正如上述代码，对于任何随机输入，我们将每个元素变成一个非负数。 此外，依据概率原理，每行总和为1。

3.3 定义模型

1. 定义softmax操作后，我们可以实现softmax回归模型。
2. 将数据传递到模型之前，我们使用reshape函数将每张原始图像展平为向量。

• reshape(-1,1)：这里的-1被理解为unspecified value，意思是未指定为给定的。只需要特定的列数，行数多少无所谓，用-1代替（-1可以理解为一个正整数通配符，它代替任何整数）。
• shape[0]：表示矩阵的行数。
  对于图像来说：image.shape[0]——图片高度；image.shape[1]——图片宽度；image.shape[2]——图片通道数。
  对于矩阵来说：shape[0]：表示矩阵的行数；shape[1]：表示矩阵的列数。

def net(X):
	# 权重为784×10的矩阵，这里将原始图像的列数大小转换为权重w矩阵的行数大小
	# 模型简单看来为：softmax(wx' + b)
    return softmax(torch.matmul(X.reshape((-1, W.shape[0])), W) + b)

3.4 定义损失函数

目前分类问题的数量远远超过回归问题的数量，这里采用交叉熵损失函数，交叉熵采用真实标签的预测概率的负对数似然。

1. 创建数据样本y_hat，包括2个样本在3个类别的概率，以及对应的标签y。
2. 通过y知道第一个样本中第一类是正确的预测，第二个样本中第三类是正确的预测。
3. 将y作为y_hat的索引，选择第一个样本第一类的概率和第二个样本第三类的概率。
   

实现交叉熵损失函数

• len(x)：获取x的长度
• range(x)：生成从0开始，小于参数x的整数序列

# 定义交叉熵损失函数
def cross_entropy(y_hat, y):
    return - torch.log(y_hat[range(len(y_hat)), y]) 

cross_entropy(y_hat, y)

3.5 分类精度

给定预测概率分布y_hat，当我们必须输出硬预测（hard prediction）时， 我们通常选择预测概率最高的类。

1. 当预测与标签分类y一致时，即是正确的。
2. 分类精度即正确预测数量与总预测数量之比。
3. y_hat是矩阵，假定第二个维度存储每个类的预测分数。
4. 使用argmax获得每行中最大元素的索引来获得预测类别。
5. 将预测类别与真实y元素进行比较。
6. 通过"=="比较，结果为包含0（错）和1（对）的张量，求和得到正确预测的数量。

• argmax()：返回的是最大数的索引.argmax有一个参数axis,默认是0,表示第几维的最大值。

def accuracy(y_hat, y):  #@save
    """计算预测正确的数量"""
    # len是查看矩阵的行数
    # y_hat.shape[1]就是去列数
    if len(y_hat.shape) > 1 and y_hat.shape[1] > 1:
    	# 第2个维度为预测标签，取最大元素
        y_hat = y_hat.argmax(axis=1) 

	#  #将y_hat转换为y的数据类型然后作比较，cmp函数存储bool类型
    cmp = y_hat.type(y.dtype) == y 
    return float(cmp.type(y.dtype).sum()) #将正确预测的数量相加

1. y_hat和y分别作为预测的概率分布和标签。
2. 第一个样本的预测类别是2（该行的最大元素为0.6，索引为2），这与实际标签0不一致。第二个样本的预测类别是2（该行的最大元素为0.5，索引为2），这与实际标签2一致。 因此，这两个样本的分类精度率为0.5。

对于任意数据迭代器data_iter可访问的数据集， 我们可以评估在任意模型net的精度。

• with torch.no_grad()：不使用时，此时有grad_fn=属性，表示计算的结果在一计算图当中，可以进行梯度反传等操作。使用时，表明当前计算不需要反向传播，使用之后，强制后边的内容不进行计算图的构建。
• isinstance()：python中的一个内置函数，作用：判断一个函数是否是一个已知类型，类似type()。
  isinstance (object , classinfo)判断两个类型是否相同。
  • object：实例对象；
  • classinfo：可以是直接或间接类名、基本类型或由它们组成的元组；
  • 返回值：如果对象的类型与参数二(classinfo)的类型相同返回true，否则false。
• torch.nn.Module()：它是所有的神经网络的根父类， 神经网络必然要继承。
• net.eval()：pytorch中用来将神经网络设置为评估模型的方法。
  • 评估模式下，网络的参数不会被更新，dropout和batch normalization层的行为也会有所不同，以便模型更好地进行预测。
  • 评估模式下计算图不会被跟踪，这样可以节省内存使用，提升性能。
• y.numel()：Python中的张量计算方法，用于存储新的张量并存储在内存中。可以通过指定形状的shape属性来访问张量的形状。

def evaluate_accuracy(net, data_iter): #@save
	"""计算在指定数据集上模型的精度"""
	# 判断模型是否为深度学习模型
	if isinstance(net, torch.nn.Module):
		net.eval() # 将模型设置为评估模式
	metric = Accumulator(2) # metric：度量，累加正确预测数、预测总数
	
	# 梯度不需要反向传播
	with torch.no_grad():
		# 每次从迭代器中拿出一个X和y
		for X, y in data_iter:
		
			# metric[0, 1]分别为网络预测正确的数量和总预测的数量
			# nex(X)：X放在net模型中进行softmax操作
			# numel()函数：返回数组中元素的个数，在此可以求得样本数
			metric.add(accuracy(net(X), y), y.numel()) 
	
	# # metric[0, 1]分别为网络预测正确数量和总预测数量
	return metric[0] / metric[1]

定义一个实用程序类Accumulator，用于对多个变量进行累加，Accumulator实例中创建了2个变量， 分别用于存储正确预测的数量和预测的总数量。

• __init__()：创建一个类，初始化类实例时就会自动执行__init__()方法。该方法的第一个参数为self，表示的就是类的实例。self后面跟随的其他参数就是创建类实例时要传入的参数。
• reset()；重新设置空间大小并初始化。
• __getitem__()：接收一个idx参数，这个参数就是自己给的索引值，返回self.data[idx]，实现类似数组的取操作。

class Accumulator: #@save
	"""在n个变量上累加"""
	# 初始化根据传进来n的大小来创建n个空间，全部初始化为0.0
	def __init__(self, n):
		self.data = [0.0] * n

	# 把原来类中对应位置的data和新传入的args做a + float(b)加法操作然后重新赋给该位置的data，从而达到累加器的累加效果
	def add(self, *args):
		self.data = [a + float(b) for a, b in zip(self.data, args)]

	# 重新设置空间大小并初始化。
	def reset(self):
		self.data = [0.0] * len(self.data)
		
	# 实现类似数组的取操作
	def __getitem__(self, idx):
		return self.data[idx]

由于我们使用随机权重初始化net模型， 因此该模型的精度应接近于随机猜测。 例如在有10个类别情况下的精度为0.1。

3.6 训练

1. 定义一个函数来训练一个迭代周期。
2. updater是更新模型参数的常用函数，它接受批量大小作为参数。 它可以是d2l.sgd函数，也可以是框架的内置优化函数。

def train_epoch_ch3(net, train_iter, loss, updater):  #@save
    """训练模型一个迭代周期（定义见第3章）"""
    # 判断net模型是否为深度学习类型，将模型设置为训练模式
    if isinstance(net, torch.nn.Module):
        net.train() # 要计算梯度
        
    # Accumulator(3)创建3个变量：训练损失总和、训练准确度总和、样本数
    metric = Accumulator(3)
    for X, y in train_iter:
        # 计算梯度并更新参数
        y_hat = net(X)
        l = loss(y_hat, y)

		# 判断updater是否为优化器
        if isinstance(updater, torch.optim.Optimizer):
            # 使用PyTorch内置的优化器和损失函数
            updater.zero_grad() #把梯度设置为0
            l.mean().backward() #计算梯度
            updater.step()		#自更新
        else:
            # 使用定制的优化器和损失函数
            # 自我实现的话，l出来是向量，先求和再求梯度
            l.sum().backward()
            updater(X.shape[0])
        metric.add(float(l.sum()), accuracy(y_hat, y), y.numel())
    # 返回训练损失和训练精度，metric的值由Accumulator得到
    return metric[0] / metric[2], metric[1] / metric[2]

定义一个在动画中绘制数据的实用程序类Animator

class Animator:  #@save
    """在动画中绘制数据"""
    def __init__(self, xlabel=None, ylabel=None, legend=None, xlim=None,
                 ylim=None, xscale='linear', yscale='linear',
                 fmts=('-', 'm--', 'g-.', 'r:'), nrows=1, ncols=1,
                 figsize=(3.5, 2.5)):
        # 增量地绘制多条线
        if legend is None:
            legend = []
        d2l.use_svg_display()
        self.fig, self.axes = d2l.plt.subplots(nrows, ncols, figsize=figsize)
        if nrows * ncols == 1:
            self.axes = [self.axes, ]
        # 使用lambda函数捕获参数
        self.config_axes = lambda: d2l.set_axes(
            self.axes[0], xlabel, ylabel, xlim, ylim, xscale, yscale, legend)
        self.X, self.Y, self.fmts = None, None, fmts

    def add(self, x, y):
        # 向图表中添加多个数据点
        if not hasattr(y, "__len__"):
            y = [y]
        n = len(y)
        if not hasattr(x, "__len__"):
            x = [x] * n
        if not self.X:
            self.X = [[] for _ in range(n)]
        if not self.Y:
            self.Y = [[] for _ in range(n)]
        for i, (a, b) in enumerate(zip(x, y)):
            if a is not None and b is not None:
                self.X[i].append(a)
                self.Y[i].append(b)
        self.axes[0].cla()
        for x, y, fmt in zip(self.X, self.Y, self.fmts):
            self.axes[0].plot(x, y, fmt)
        self.config_axes()
        display.display(self.fig)
        display.clear_output(wait=True)

3. 实现一个训练函数，它会在train_iter访问到的训练数据集上训练一个模型net。
4. 该训练函数将会运行多个迭代周期（由num_epochs指定）。

• assert()：断言函数，当表达式为真时，程序继续往下执行，只是判断，不做任何处理；当表达式为假时，抛出AssertionError错误，并将 [参数] 输出

def train_ch3(net, train_iter, test_iter, loss, num_epochs, updater):  #@save
    """训练模型（定义见第3章）"""
    animator = Animator(xlabel='epoch', xlim=[1, num_epochs], ylim=[0.3, 0.9],
                        legend=['train loss', 'train acc', 'test acc'])
                     
    # num_epochs：训练次数
    for epoch in range(num_epochs):
    	# train_epoch_ch3：训练模型，返回准确率和错误度
        train_metrics = train_epoch_ch3(net, train_iter, loss, updater)

		# 在测试数据集上评估精度
        test_acc = evaluate_accuracy(net, test_iter)
        
        animator.add(epoch + 1, train_metrics + (test_acc,))
    train_loss, train_acc = train_metrics
    assert train_loss < 0.5, train_loss
    assert train_acc <= 1 and train_acc > 0.7, train_acc
    assert test_acc <= 1 and test_acc > 0.7, test_acc

5. 使用小批量随机梯度下降来优化模型的损失函数，设置学习率为0.1。

lr = 0.1

def updater(batch_size):
    return d2l.sgd([W, b], lr, batch_size)

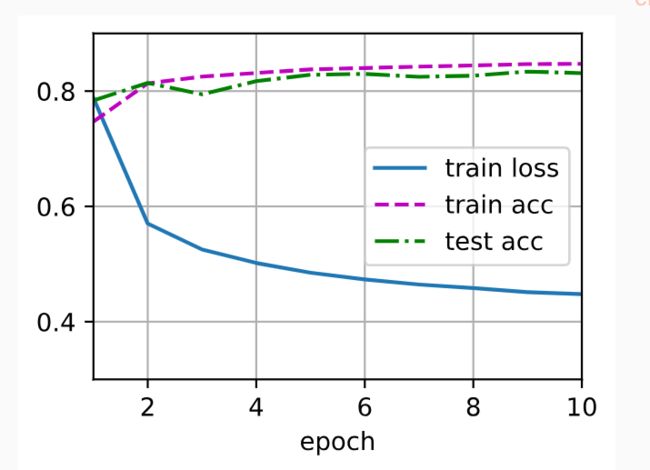
6. 训练模型10个迭代周期，其中迭代周期（num_epochs）和学习率（lr）都是可调节的超参数。

num_epochs = 10
train_ch3(net, train_iter, test_iter, cross_entropy, num_epochs, updater)

3.7 预测

训练已完成的模型可以来对准备好图像进行分类预测，给定一系列图像，我们将比较它们的实际标签（文本输出的第一行）和模型预测（文本输出的第二行）。

def predict_ch3(net, test_iter, n=6):  #@save
    """预测标签（定义见第3章）"""
    for X, y in test_iter:
        break
    trues = d2l.get_fashion_mnist_labels(y) # 实际标签
    preds = d2l.get_fashion_mnist_labels(net(X).argmax(axis=1)) 预测标签，取最大化概率
    titles = [true +'\n' + pred for true, pred in zip(trues, preds)]
    d2l.show_images(
        X[0:n].reshape((n, 28, 28)), 1, n, titles=titles[0:n])

predict_ch3(net, test_iter)

3.8 小结

• 借助softmax回归，我们可以训练多分类的模型。
• 训练softmax回归循环模型与训练线性回归模型非常相似：先读取数据，再定义模型和损失函数，然后使用优化算法训练模型。大多数常见的深度学习模型都有类似的训练过程。

4. softmax回归的简洁实现

1. 通过深度学习框架的高级API也能更方便地实现softmax回归模型。
2. 使用Fashion-MNIST数据集，并保持批量大小为256。

import torch
from torch import nn
from d2l import torch as d2l

batch_size = 256
train_iter, test_iter = d2l.load_data_fashion_mnist(batch_size)

4.1 初始化模型参数

1. softmax回归的输出层是一个全连接层。
2. 只需在Sequential中添加一个带有10个输出的全连接层。（在这里Sequential并不是必要的， 但它是实现深度模型的基础。）
3. 以均值0和标准差0.01随机初始化权重。

# PyTorch不会隐式地调整输入的形状。因此，我们在线性层前定义了展平层（flatten），来调整网络输入的形状
# Flatten()将任何维度的tensor转化为2D的tensor
# Linear(784, 10)定义线性层，输入是784，输出是10
# nn.Sequential:一个时序容器。Modules 会以他们传入的顺序被添加到容器中
net = nn.Sequential(nn.Flatten(), nn.Linear(784, 10))

def init_weights(m):
    if type(m) == nn.Linear:
        # normal_：正态分布
        nn.init.normal_(m.weight, std=0.01)

# apply()：当一个函数的参数存在于一个元组或者一个字典中时，用来间接的调用这个函数，并肩元组或者字典中的参数按照顺序传递给参数
net.apply(init_weights);

4.2 重新审视softmax的实现

1. softmax函数的分母或分子可能变成无穷大，需要优化。
2. 这里没有将softmax概率传递到损失函数中， 而是在交叉熵损失函数中传递未规范化的预测，并同时计算softmax及其对数。

loss = nn.CrossEntropyLoss(reduction='none')

4.3 优化算法

1. 使用学习率为0.1的小批量随机梯度下降作为优化算法。

trainer = torch.optim.SGD(net.parameters(), lr=0.1)

4.4 训练

num_epochs = 10
d2l.train_ch3(net, train_iter, test_iter, loss, num_epochs, trainer)

4.5 小结

1. 使用深度学习框架的高级API，我们可以更简洁地实现softmax回归。

参考资料：
[1]动手学深度学习：http://zh-v2.d2l.ai/index.html
[2]跟李沐学AI：https://space.bilibili.com/1567748478
[3]百度百科