【栈和队列】的特性以及基本接口的实现

目录

一、栈

1.1 栈的概念

1.2 栈的接口实现

二、队列

2.1 队列的概念

2.2 队列的接口实现

2.3 栈和队列的区别

三、栈和队列LeetCode练习

3.1 力扣_232.用栈实现队列

3.2 力扣_225.用队列实现栈

3.3 力扣_622.设计循环队列

3.4 力扣_20.有效的括号

---

一、栈

第一次学习数据结构的小伙伴们不要把栈想的很难，实际上挺简单的。只要搞清楚一点：“后进先出，先进后出” 就OK了！

1.1 栈的概念

对于逻辑关系为“一对一”的数据，除了用顺序表和链表存储外，还可以用栈结构存储。

栈是一种“特殊”的线性存储结构，它的特殊之处体现在以下两个地方：

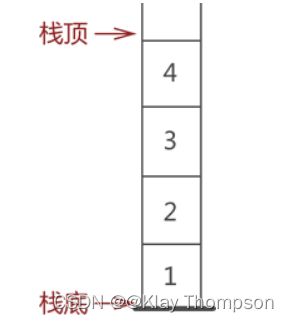
1、元素进栈和出栈的操作只能从一端完成，另一端是封闭的，如下图所示：

 通常，我们将元素进栈的过程简称为“入栈”、“进栈”或者“压栈”；将元素出栈的过程简称为“出栈”或者“弹栈”。

2、栈中无论存数据还是取数据，都必须遵循“先进后出”的原则，即最先入栈的元素最先出栈。以上图的栈为例，很容易可以看出是元素 1 最先入栈，然后依次是元素 2、3、4 入栈。在此基础上，如果想取出元素 1，根据“先进后出”的原则，必须先依次将元素 4、3、2 出栈，最后才能轮到元素 1 出栈。

我们习惯将栈的开口端称为栈顶，封口端称为栈底。

由此我们可以对栈存储结构下一个定义：栈是一种“只能从一端存取元素，且存取过程必须遵循‘先进后出’原则”的线性存储结构。

1.2 栈的接口实现

//Stack.h文件


#pragma once


#include 
#include 
#include 
#include 

typedef int DataType;
typedef struct Stack
{
	DataType* data;
	int top;
	int capacity;
}ST;


//初始化栈
void STInit(ST* pst);

//入栈
void STPush(ST* pst, DataType x);

//出栈
void STPop(ST* pst);

//栈的销毁
void STDestory(ST* pst);

//得到栈顶元素
DataType STGetTop(ST* pst);

//判断栈是否为空
bool STEmpty(ST* pst);

//栈的大小——元素个数
int STSize(ST* pst);

//Stack.c文件


#include "Stack.h"

void STInit(ST* pst)
{
	assert(pst);
	pst->data = NULL;
	pst->top = 0;
	pst->capacity = 0;
}

void STPush(ST* pst, DataType x)
{
	assert(pst);

	//扩容
	if (pst->top == pst->capacity)
	{
		int newCapacity = pst->capacity == 0 ? 4 : pst->capacity * 2;
		DataType* tmp = (DataType*)realloc(pst->data, sizeof(DataType) * newCapacity);
		if (tmp == NULL)
		{
			perror("realloc fail!\n");
			return;
		}
		pst->data = tmp;
		pst->capacity = newCapacity;
	}

	//入栈
	pst->data[pst->top] = x;
	pst->top++;
}

void STPop(ST* pst)
{
	assert(pst);

	assert(!STEmpty(pst));

	pst->top--;
}

void STDestory(ST* pst)
{
	assert(pst);
	free(pst->data);
	pst->data = NULL;
	pst->top = 0;
	pst->capacity = 0;
}



DataType STGetTop(ST* pst)
{
	assert(pst);
	assert(!STEmpty(pst));

	return pst->data[pst->top - 1];
}

bool STEmpty(ST* pst)
{
	assert(pst);
	return pst->top == 0;
}



int STSize(ST* pst)
{
	assert(pst);
	return pst->top;
}

二、队列

2.1 队列的概念

队列用来存储逻辑关系为“一对一”的数据，是一种“特殊”的线性存储结构。和顺序表、链表相比，队列的特殊性体现在以下两个方面：

1、元素只能从队列的一端进入，从另一端出去，如下图所示： 

通常，我们将元素进入队列的一端称为“队尾”，进入队列的过程称为“入队”；将元素从队列中出去的一端称为“队头”，出队列的过程称为“出队”。

2、队列中各个元素的进出必须遵循“先进先出”的原则，即最先入队的元素必须最先出队。

以上图所示的队列为例，从各个元素在队列中的存储状态不难判定，元素 1 最先入队，然后是元素 2 入队，最后是元素 3 入队。如果此时想将元素 3 出队，根据“先进先出”原则，必须先将元素 1 和 2  依次出队，最后才能轮到元素 3 出队。

2.2 队列的接口实现

//Queue.h文件


#pragma once


#include 
#include 
#include 
#include 	

typedef int DataType;
typedef struct QNode
{
	DataType data;
	struct QNode* next;
}QNode;

typedef struct Queue
{
	QNode* phead;
	QNode* ptail;
	int size;
}Queue;

//初始化队列
void QueueInit(Queue* pq);

//销毁队列
void QueueDestory(Queue* pq);

//入队
void QueuePush(Queue* pq, DataType x);


//出队
void QueuePop(Queue* pq);

//队头元素
DataType QueueFront(Queue* pq);

//队尾元素
DataType QueueBack(Queue* pq);

//队列的大小
int QueueSize(Queue* pq);

//判断队列是否为空
bool QueueEmpty(Queue* pq);

//Queue.c文件


#include "Queue.h"

void QueueInit(Queue* pq)
{
	assert(pq);
	pq->phead = NULL;
	pq->ptail = NULL;
	pq->size = 0;
}

void QueueDestory(Queue* pq)
{
	assert(pq);
	QNode* cur = pq->phead;
	while (cur)
	{
		QNode* next = cur->next;
		free(cur);
		cur = next;
	}
	pq->phead = NULL;
	pq->ptail = NULL;
	pq->size = 0;
}

void QueuePush(Queue* pq, DataType x)
{
	assert(pq);
	QNode* newnode = (QNode*)malloc(sizeof(QNode));
	if (newnode == NULL)
	{
		perror("malloc fail!\n");
		return;
	}
	newnode->data = x;
	newnode->next = NULL;


	if (pq->phead == NULL)
	{
		assert(pq->ptail == NULL);
		pq->phead = pq->ptail = newnode;
	}
	else
	{
		pq->ptail->next = newnode;
		pq->ptail = newnode;
	}
	pq->size++;
}

void QueuePop(Queue* pq)
{
	assert(pq);

	//没有节点
	assert(!QueueEmpty(pq));
	//只有一个节点
	if (pq->phead->next == NULL)
	{
		free(pq->phead);
		pq->phead = NULL;
		pq->ptail = NULL;
	}

	else
	{
		QNode* next = pq->phead->next;
		free(pq->phead);
		pq->phead = next;
	}
	pq->size--;
}

DataType QueueFront(Queue* pq)
{
	assert(pq);
	assert(pq->phead);
	return pq->phead->data;
}

DataType QueueBack(Queue* pq)
{
	assert(pq);
	assert(pq->phead);
	return pq->ptail->data;
}

int QueueSize(Queue* pq)
{
	assert(pq);
	return pq->size;
}

bool QueueEmpty(Queue* pq)
{
	assert(pq);
	return pq->phead == NULL && pq->ptail == NULL;
}

2.3 栈和队列的区别

栈和队列不要混淆，栈是一端开口、另一端封口，元素入栈和出栈遵循“先进后出”原则；队列是两端都开口，但元素只能从一端进，从另一端出，且进出队列遵循“先进先出”的原则。

三、栈和队列LeetCode练习

3.1 力扣_232.用栈实现队列

typedef struct {
    ST PushST;
    ST PopST;
} MyQueue;


MyQueue* myQueueCreate() {
    MyQueue* obj = (MyQueue*)malloc(sizeof(MyQueue));
    STInit(&obj->PushST);
    STInit(&obj->PopST);

    return obj;
}

void myQueuePush(MyQueue* obj, int x) {
    STPush(&obj->PushST, x);
}

int myQueuePop(MyQueue* obj) {
    int ret = myQueuePeek(obj);
    STPop(&obj->PopST);
    return ret;
}

int myQueuePeek(MyQueue* obj) {
    if(STEmpty(&obj->PopST))
    {
        while(!STEmpty(&obj->PushST))
        {
            STPush(&obj->PopST, STGetTop(&obj->PushST));
            STPop(&obj->PushST);
        }
    }
    return STGetTop(&obj->PopST);
}

bool myQueueEmpty(MyQueue* obj) {
    return STEmpty(&obj->PushST) && STEmpty(&obj->PopST);
}

void myQueueFree(MyQueue* obj) {
    STDestory(&obj->PushST);
    STDestory(&obj->PopST);
    free(obj);
}

3.2 力扣_225.用队列实现栈

 

typedef struct {
    Queue q1;
    Queue q2;

} MyStack;


MyStack* myStackCreate() {
    MyStack* obj = (MyStack*)malloc(sizeof(MyStack));
    QueueInit(&obj->q1);
    QueueInit(&obj->q2);

    return obj;
}

void myStackPush(MyStack* obj, int x) {
    if(!QueueEmpty(&obj->q1))
    {
        QueuePush(&obj->q1, x);
    }
    else{
        QueuePush(&obj->q2, x);
    }
}

int myStackPop(MyStack* obj) {
    Queue* EmptyQ = &obj->q1;
    Queue* NoEmptyQ = &obj->q2;
    if(!QueueEmpty(&obj->q1))
    {
        EmptyQ = &obj->q2;
        NoEmptyQ = &obj->q1;
    }

    while(QueueSize(NoEmptyQ) > 1)
    {
        QueuePush(EmptyQ, QueueFront(NoEmptyQ));
        QueuePop(NoEmptyQ);
    }
    int top = QueueFront(NoEmptyQ);
    QueuePop(NoEmptyQ);
    return top;
}

int myStackTop(MyStack* obj) {
    if(!QueueEmpty(&obj->q1))
    {
        return QueueBack(&obj->q1);
    }
    else
    {
        return QueueBack(&obj->q2);
    }
}

bool myStackEmpty(MyStack* obj) {
    return QueueEmpty(&obj->q1) && QueueEmpty(&obj->q2);
}

void myStackFree(MyStack* obj) {
    QueueDestory(&obj->q1);
    QueueDestory(&obj->q2);

    free(obj);
}

3.3 力扣_622.设计循环队列

typedef struct {
    int front;
    int rear;
    int k;
    int* a;
} MyCircularQueue;


MyCircularQueue* myCircularQueueCreate(int k) {
    MyCircularQueue* obj = (MyCircularQueue*)malloc(sizeof(MyCircularQueue));
    obj->a = (int*)malloc(sizeof(int) * (k + 1));
    if(obj == NULL)
    {
        perror("malloc fail!\n");
        return NULL;
    }
    obj->front = obj->rear = 0;
    obj->k = k;

    return obj;
}
bool myCircularQueueIsFull(MyCircularQueue* obj) {
    return (obj->rear + 1) % (obj->k + 1) == obj->front;
}

bool myCircularQueueIsEmpty(MyCircularQueue* obj) {
    return obj->front == obj->rear;
}


bool myCircularQueueEnQueue(MyCircularQueue* obj, int value) {
    if(myCircularQueueIsFull(obj))
        return false;
    obj->a[obj->rear] = value;
    obj->rear++;
    obj->rear %= (obj->k+1);
    return true;
}

bool myCircularQueueDeQueue(MyCircularQueue* obj) {
    if(myCircularQueueIsEmpty(obj))
    {
        return false;
    }
    obj->front++;
    obj->front %= (obj->k+1);
    return true;

}

int myCircularQueueFront(MyCircularQueue* obj) {
    if(!myCircularQueueIsEmpty(obj))
        return obj->a[obj->front];
    else
        return -1;
}

int myCircularQueueRear(MyCircularQueue* obj) {
    if(!myCircularQueueIsEmpty(obj))
        return obj->a[(obj->rear + obj->k) % (obj->k + 1)];
    else
        return -1;
}


void myCircularQueueFree(MyCircularQueue* obj) {
    free(obj->a);
    free(obj);
}

3.4 力扣_20.有效的括号

bool isValid(char * s)
{
    ST st;
    STInit(&st); 
    while(*s)
    {
        if(*s == '(' || *s == '[' || *s == '{')
        {
            STPush(&st, *s);
        }
        else
        {
            if(STEmpty(&st))
            {
                STDestory(&st);
                return false;
            }
            char top = STGetTop(&st);
            STPop(&st);
            if(*s == ')' && top != '('
            || *s == ']' && top != '['
            || *s == '}' && top != '{')
            {
                STDestory(&st);
                return false;
            }
        }
        s++;
    }
    bool ret = STEmpty(&st);
    STDestory(&st);
    return ret;
}