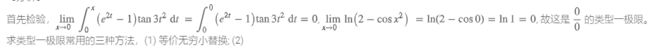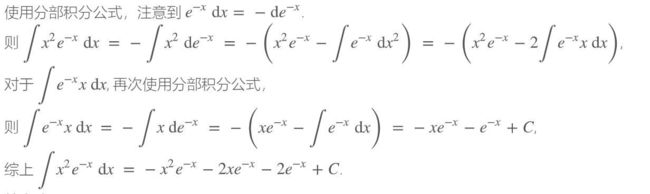知能行考研数学的高数部分怎么样?大一可以用吗?
目录
方法一等价替换
方法二泰勒公式
方法三洛必达法则
一、值得一看的网课
二、带着问题听课
三、如何调整在学习高数时的心态
四、总结
我上大学的时候,面对这两部分知识点,也学得很吃力,尤其是微积分
但是后来我学明白之后,发现其实也不过如此
如果你和我一样,数学基础并不好,或者一开始学习高数有困难,那么这篇极限和微积分的保姆级教学,你真的应该仔细看一下。
极限和微积分确实很难,但是大一高数对于我们的要求其实并不高,只要我们会用知识点或者公式做题就行了,有的题目就是专门为那一个知识点出的,并不需要我们有太深刻的理解。
就拿极限来说,其实想学好并不难,你只要掌握他的三种类型出题方式,基本上就可以拿捏。
下面我尝试给你讲解清楚该如何着手学习。
给大家分享一个我很喜欢的思维导图,是我从【知能行考研数学】网站上找来的
这个思维导图总结的特别清楚,这三类方法一下午就能掌握,大一考试的极限保证能口算!
其实函数的极限就是三种类型的计算,类型一就是 00 , ∞∞ ,0 ⋅ ∞ 这三种,这种的解题方法就是三种方法,分别是等价无穷小替换,泰勒公式和洛必达法则。
第二种类型就是 ∞−∞ ,这种就是通过通分和乘除某个式子化成类型一。
第三种类型就是 1∞ ,这个需要运用到 ()limx→0(1+x)1x=e ;然后是 00 , ∞0 ,这种就是需要写成指数函数形式,化成类型一。
可以看到,我们处理函数极限的方法,百变不离其宗。都是化成类型一然后利用那三种方法。我看到这个思维导图,是在考研复习走了很多弯路之后,看到的那一瞬间忽然就有醍醐灌顶的感觉。
我高数大一学的就很痛苦,有很多知识在大一的时候都没有学明白,到考研了,还是没有学明白。然后发现知能行竟然有大一版!可惜我大一的时候不知道知能行,如果我大一就开始,可能现在也不至于费劲考研,直接可以达到保研的分数了。
印象最深的是,知能行的知识点总结得特别清楚,理解透彻,比自己瞎找省好多时间。
下面我把在知能行学到的方法给大家讲一下。所有的题解、知识点截图都是我在知能行系统中学习的时候留下来的。
我先来讲讲我对三种求极限的方法的理解,其余部分的学习也是要首先知道学习方向,以终为始,然后学习其中做题的主要方法,你就可以学好高数,接下来我们就来说说这三种方法分别是什么:
方法一等价替换
你一定要记住下面这个图。
你知道为什么要用狗头代表吗,因为它可以是任何连续的函数。可以是 x ,也可以是sin x,
(1-cos x),f(x)。只要是连续的函数就可以。
方法二泰勒公式
你一定要学会,这个是求极限的最简单的方法,虽然老师主要教方法一,但是泰勒公式解极限非常丝滑快速。主要是下面的及格公式,打死也要背住。
注意上图中标红的部分,一般你只需要用红色部分就可以了。下面我举个知能行上面的例子,你就知道用泰勒公式解极限有多么的顺滑了。
你可以思考一下这个题目,用等价无穷小替换是非常麻烦的,但是如果你用泰勒公式,神奇的事情就出现了,下面我将给出知能行上的题解:
我上面讲过,类型二和类型三都要转化成类型一,这题也不例外。通过分子分母有理化可以判断这是类型一中的00,大家在做题目之前一定要先判断类型,因为很多同学都喜欢洛必达,但是除了和00和∞∞其他形式的极限都不能直接用洛必达。上面转换过来之后知能行就是利用泰勒公式进行化简
看上面最后一步, ex 的泰勒展开可以和后面的消掉,大家可能会担心消不掉,放心,肯定可消掉,题目肯定会消除完,其实等价变化公式,就是上面的狗头图,里面就是泰勒公示的特殊情况。
下面还是利用泰勒公式进行变换,完成解题。是不是很方便。
因为知能行是个性化学习,每个人练的不一样,所以如果我讲的不够全面,是因为知能行会抓住我的薄弱点来训练。你去学习的时候,就会根据你的薄弱点来了。
很多人上课其实是听得懂的,但做题就有困难,因为有隐藏的薄弱点。知能行会找到你题目做不会的根本原因,然后逐一帮你打通薄弱点,最后吃透所有的知识点。
在找到你的问题之后,知能行就是专注于帮你吃透你没有掌握的薄弱点。
方法三洛必达法则
很多人做极限只会用洛必达,但是洛必达的使用是有条件的,就是我上面说的:除了和00和∞∞其他形式的极限都不能直接用洛必达。因此你想用洛必达就必须判断极限的类型。这是知能行上的洛必达知识点:
下面我举个知能行上的例子:
这道题也是比较复杂的,首先判断极限类型:
然后看到可以用洛必达之后,也不能急着用,还要把他进行相应的化简,才可以使用洛必达。
如果你想学习其他部分的知识点,知能行上面都有。不管你基础怎么样,它都可以帮你循序渐进的进行学习,练会为止。微积分的学习也是一样的,先确定学习方向,以终为始,遇到问题解决问题,然后你的学习效率才会更高,效果才会更好。
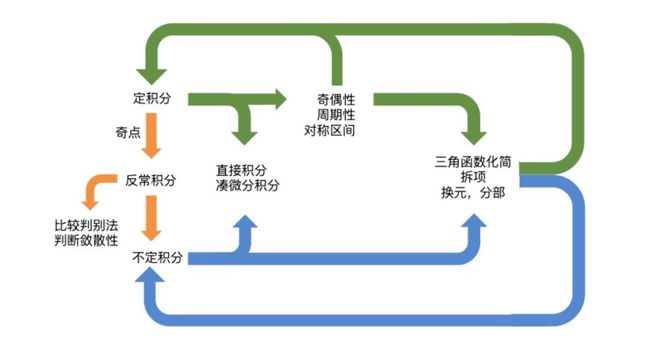
接下来我们讲积分
下面是在知能行网站上找到的关于积分的思维导图
比较初级的积分其实就是解积分,解积分其实方法也就那么多,我们知道导数和积分是相对应的,大家高数书上肯定有一个导数积分对照表,如果没有就是下面这张,大家一定要把他背的滚瓜烂熟。
因为大一的积分考察的并不是很难,背住这个表,可以解决很多问题,这个也叫直接积分法。
那有的同学可能会说,这个我们都知道,可是还是不会做题
要想把积分题目做好,知道上面那张表只能做一些基础题目,考试肯定会有一定的变形的,所以你要掌握一些根本方法,下面我就通过知能行上的一些例题把这些方法教给你们。
【分步积分法】【凑微分积分法】
这里我们首先要知道两个基本公式
这个公式进行训练之前,可以在知能行的复习提示里找到。我们可以熟悉一下这个公式,因为待会做题的时候会用到。
比如,下面就是知能行给出的一道题目:
这其实是很基础的一道题目,大家可以试一下如果在我没有给你提示的情况下,你该怎么做,还是会选择用直接积分法吗?
这个很明显的就是可以用分步积分法:
知能行给出的分析:
然后按照这个公式,再把两边给带入进去,就可以很快的解题了。
我们可以很清楚的看到,知能行在分析的时候就说,是不能凑微分的,这是知识点,大家可以记下来。
当然,很多同学可能的难点就是不知道谁是u,谁是v,我的观点是,容易求导被消除,谁就是u,比如这道题目里面, x2 求两次导之后就没有了,就可以给后面的计算带来方便,如果求导之后越来越复杂,那后面的式子也就会越来越复杂。
看到这里,你是不是感觉,知能行给出的解题方法都很好用,很高效
你没有感觉错,知能行会教会你很多实用的技巧。
知能行里面的所有题目都是经过仔细分析的,结合题目特征,深化知识体系而开发设计出来的一款高数学习备考系统,系统内囊括了课本里的知识点、习题册里的技巧、老师传授的思路,并做了高效、科学的结合,可以最大程度上提高高数学习的效率。
比如像下面这样的解题技巧,在知能行里面有很多。
它利用大数据分析,实现考点和难点的均匀覆盖,精细化出题,分专题复习。你不需要做所有的题,系统会自动选择对你提高最快的题目
在思维导图中,我们还看到有另外两种方法,分别是换元法和拆项积分法,这两个方法也是解积分常用的方法。
下面我就通过在知能行上找的例题来给大家简单的讲解一下:
【换元法】【拆项积分法】
同样,知能行会先给出关于这一部分要用到的知识点,大家就不用费事翻书了
大家可以思考一下这个题目。
知能行的解析指出如果观察到积分中多次出现一样的函数,就可以考虑使用换元法化简,这道题目多次出现lnIxI,于是,我们就可以令lnIxI=t。
我们可以看到,化简之后,就是我们熟悉的积分形式,这个形式的积分如果无法直接积分,就可以考虑是不是分步积分
化简到这一步,已经是我们想要的样子了,前面一项不用管,后面一项很明显可以使用拆项进行化简。
这个就是最后积分的结果。大家明白了吗?
最后知能行对于包含三角函数求积分会进行专门的训练,因为包含三角函数的积分确实难算。
【三角函数求积分】
三角函数求积分这一部分可以说是比较难的,我说一下知能行上教我的几个特殊的题型,大家如果学会了,那做题速度快很多。
【sin x和cos x的偶次幂】
还是老样子,做题之前,知能行会带你复习相关的知识点和要用到的公式
下面这道题是知能行上面比较经典的题目:
下面是知能行给出的解析:
你是不是觉得这样就结束了,其实你远远没有达到知能行的标准,知能行会反复检测,确保你吃透知识点
知能行判断你有没有吃透一个知识点是非常严谨的,并不是说你做对了包含这个知识点的题目,就确定你做对了,在后面的做题中,他会给你推送包含该知识点的不同考法,不同组合的题目。
比如,我们做完上面那道题之后,知能行为了检测你有没有真的学会,会给你推送下面这道题,会用相似的解法,但是会有一定的变形,这就是知能行的知识点精细化拆分+组合的出题策略
方法是一样的:
最重要的就是他会自动帮你复习。大家都知道英语有艾宾浩斯遗忘曲线,知能行也李永乐这一点。因此,不会存在知识点没有吃透的情况。
就算你以后遗忘了,知能行会帮助你重新进行复习。你对于知识点的掌握只会越来越牢固。
【 sin2x + cos2x =1及其变形的应用】
下面的例题,是知能行想要帮你学会上面图片中第二行的变形:
这是知能行给出的解析:
再来一道训练一下:
每一道题知能行都会给出详细的解析:
知能行上还有一种比较特殊的题型就是
【含 ax+bn 和 ax+bm 】
这类题型的做题方法就是
比如下面这道题
其实上面只是积分的基础计算,关于积分的应用还有很多变形,比如下面这张思维导图也是在知能行上面找的,总结了一些比较复杂的积分应用。
总结一下,像上面的求极限三种方法,经过知能行一下午的训练基本上就可以掌握的差不多,微积分可能要花多一点的时间,但是比传统的学习方法要高效太多了。
因为我这篇高数学习教程是根据知能行的资料写的,所以文中多次提到知能行,可能大家觉得我在给他打广告,其实不管大家怎么想,能帮到大家才是我真正的目的。但是知能行确实是好东西,我觉得确实值得推广。
知能行是一本题集,但是它不仅仅是一本题集。它可以是你刷题过程的监管,展示你的各方面数据,让你对于自己的水平有一个清晰的认知。
它也可以是一本电子错题集,记录你曾经错过的地方,帮助你精准复习。
我上面给大家找的题目就是在知能行记录的我以前的错题里面找到的经典题目。
他能让你实现更精细化的训练,对于每一个章节都有细致的划分,可以缩小训练范围,达到精准训练的目的。比如函数与极限这一个部分可以分为极限1、数列极限1&2、间断点分别来训练
其实我以前做数学题也是非常的痛苦,但是开始用知能行这个刷题工具之后,我发现数学学习可以是一个非常愉快的过程,他并不是一个帮你投机的工具,而是切切实实的用科学的方法,帮你循序渐进的喜欢上数学的学习,帮你扎扎实实的提高数学成绩。他只是利用非常先进的技术,帮你数倍的提高了数学学习的效率,帮你排除数学学习的障碍,以前对于你来说非常困难的事,在用完知能行之后基本上感受不到
说完怎么做题,我还有一些学习高数的经验应该可以帮到大家,下面我就来分享一下:
一、值得一看的网课
很多同学刚上大一的时候很难跟上高数老师的节奏,这个时候课堂外的补充就显得尤为重要。
现在互联网资源这么多,网上不乏优秀的网课资源,我给你推荐一个我当年看过的。可以说是我的高数引路人。
B站宋浩老师,绝对的宝藏老师,值得去看
老师每节课,每个知识点都会在黑板上演草,这对于我们刚上大一的同学非常的友好,可以看清楚定理的推理过程,而且最重要的就是可以回放,这就比线下上课有优势,哪里不理解可以多听几遍。老师讲课的节奏我认为也对那些基础不好的同学非常的友好。
二、带着问题听课
很多人其实没有预习的习惯,但是预习是一个让你听课效率成倍提高的好习惯。
很多人期末考试的时候会开玩笑说“我要开始预习(复习)了”听到这里我们除了笑笑,还是要反思一下,为什么大家总是把做事的顺序搞反。
以我的个人经验来说,大一的课程一点也不多,大家完全有时间进行高数的预习,在上课之前,把老师要讲的课程自己通读一遍,然后把自己不会的问题都标注出来。
然后带着这些问题去听课。你会发现,你不仅上课的时候会非常的专注,因为你想找到你的问题的答案,你下课的时候还会去学习,直到搞懂这些问题。
你要学会把任务都分配到平时,然后你期末考试的时候就会非常的轻松。这些都是我和那些保研的学长交流得到的经验,非常的实用
三、如何调整在学习高数时的心态
很多人面对高数时“谈虎色变”,避而不谈,甚至连课都不愿意去听。
其实高数并没有这么可怕,但是高数这个学科的设置确实很变态,一上来就让我们这个小兵去打boss,谁都会退缩的。
面对高数学习时的心态应该是什么样子的呢?
因该是一种挑战的心态,高数的难度是我们够得着的高度,并不是高不可攀,遥不可及。如果你真的觉得做不到,那是你的目标顶的太大了,你要学会分解自己的目标。分解到你只要努力一小点就可以轻松的完成。这回给你一个积极的正反馈。
上面我提到的知能行就是一种渐进式的感觉,你能够明显感觉到自己的进步。他的机制就像是打游戏,一开始你是零级,慢慢的你刷到了一级,然后紧接着是二级,三级,这也对应着你的能力在逐步的提升
四、总结
如果你对于高数学习有很多的疑问,那么你可以关注我,我非常喜欢研究高数,我也很喜欢向大家科普高数该如何学习。
养好课前预习的习惯,把任务分配的平时,你肯定可以在期末考一个好成绩!