CORDIC算法FPGA的实现
基于CORDIC算法FPGA的实现
CORDIC算法原理利用简单的移位就实现,主要用于三角函数、双曲线、指数、对数的计算,在以二进制操作为基础的FPGA硬件中就显得尤为重要。虽然现在的fpga有了集成IP核,但是对于其基本原理还是需要关注的。
基于个人理解,本文主要对该算法进行简单推导,同时利用matlab进行仿真,并在fpga中实现。
1、CORDIC算法的推导
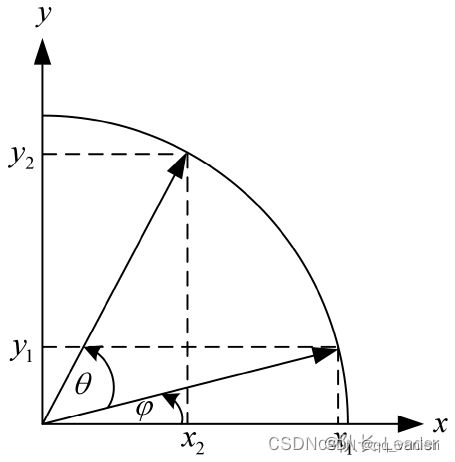
CORDIC(Coordinate Rotation Digital Computer)算法即坐标旋转数字计算方法。在网上已经有了很多推导算法,不过在这里还是给大家挑选一种重新推导下。先附上示意图如下
1.1 圆坐标系旋转公式推导
该坐标旋转在一个半径为r的圆中进行旋转(注意是一个圆坐标系,因为还有在线性坐标和双曲线坐标系中,其他坐标系推导也类似,这里不进行阐述),
那么(x1,y1)坐标可以表示为
x1=rcosφ, y1=sinφ;
(x1,y1)旋转θ角度后为(x2,y2)坐标可以表示为
x2=rcos(φ+θ)=rcosφcosθ-rsinφsinθ=x1cosθ- y1sinθ;
y2=rsin(φ+θ)=rsinφcosθ+rcosφsinθ=y1cosθ+ x1sinθ;
因此,在圆坐标系中,(x1,y1)逆时钟旋转θ角度后,得到的(x2,y2)坐标为
x2=x1cosθ- y1sinθ;
y2=x1sinθ+y1cosθ;
这个就是圆坐标系的旋转公式。通过提出因数cosθ ,方程可写成下面的形式
x2 =cosθ(x1 – y1 tanθ)
y2= cosθ(y1 + x1 tanθ)
如果去除 cosθ项,我们得到 伪旋转 方程式
x2’ =(x1 – y1 tanθ)
y2’= (y1 + x1 tanθ)
即旋转的角度是正确的,但是 x 与 y 的值增加1/cosθ 倍 ( 由于1/cosθ大于1,所以模值变大),为什么要去除cosθ,是因为去除后可以简化坐标平面旋转的计算操作。
 因此经过伪旋转之后,向量 R 的模值将增加 1/cosθ 倍。
因此经过伪旋转之后,向量 R 的模值将增加 1/cosθ 倍。
1.2CORDIC算法推导
为什么要提取cosθ公共项,并去除cosθ,其实本质是需要构造一个tanθ的函数,利用tanθ构造可在二进制中的移位的迭代参数,同时cosθ因子并不能通过适当的数学方法去除(去除该因子后文给出说明),所以要转为伪旋转。利用matlab构造tanθ和二进制移位参数表如下图所示,该参数表固定,
##matlab生成参数表
clear; close all; clc;
for i=0:15
theta = rad2deg( atan(2^(-i)) );
fprintf('i=%d\t2^-i=%.9f\ttheta=%.9f\ttanθ=%.9f\n',i,2^-i,theta,tand(theta))
end
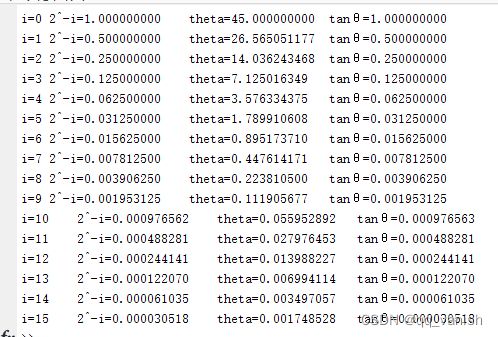
可以看出,迭代关系(二进制移位关系)和旋转角度tanθ关系,即任何旋转角度都应在表格参数中,对任意角度θ的旋转能够通过一系列连续小角度的旋转迭代 i 来完成。旋转的角度为θ,根据伪旋转公式,正切项tanθ变成了迭代移位操作。
第 1 次迭代 : 旋转 45°; 第 2 次迭代 : 旋转 26.6°, 第 3 次迭代 : 旋转 14°等。每次旋转的方向都影响到最终要旋转的累积角度,理论上-99.7°到99.7°的的范围内的任意角度都可以旋转,对于该范围之外的角度, 可使用三角恒等式转化成该范围内的角度。
旋转方向也涉及逆时钟和顺时钟,每次迭代过程需要根据旋转方向进行加或减运算。因此在伪旋转基础上,引入d 角度旋转判决因子,用于确定旋转的方向。同时也引入角度累加器概念用来在每次迭代过程中追踪累加的旋转角度Z,同时将tanθ改为二进制移位算术,伪旋转就变成如下

前面也提到过,每次伪旋转,模值都会相应增加,随着不断迭代,最终cos 45 x cos 26.5 x cos 14.03 x cos 7.125 … x cos 0.0139≈ 0.607252941,增加1/0.607=1.6476倍。引用该段证明,如下所示

如果我们已知将被执行的迭代次数,我们便可以预先计算出 1/Kn 的值,并通过将 1/Kn 与 x(n) 和 y(n)相乘来校正 x(n) 和 y(n) 的最终值。n次迭代后,最终的坐标值就只和初始的没旋转之前的坐标值x0,y0和最终旋转要达到的角度值xn,yn有关了,如下所示

乍一看公式,前面一直在说伪旋转,经过多次迭代怎么又回到看着像是最开始的圆坐标系旋转公式呢。先给出一段证明如下:
伪旋转公式为
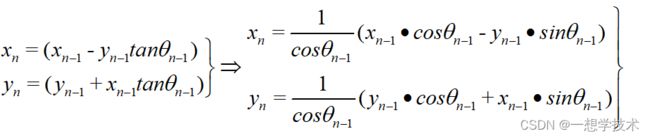
那么就有

n次迭代后,最终的坐标值就只和初始的没旋转之前的坐标值x0,y0和最终旋转要达到的角度值,注意看

可设
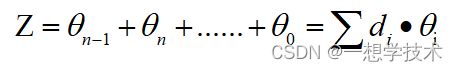
因此,等式就变为
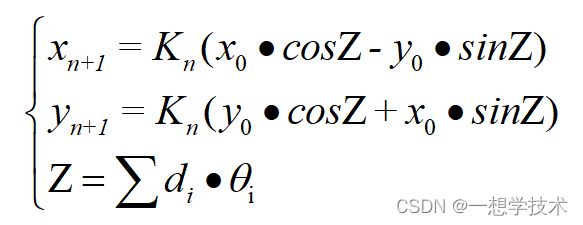
看到这里,应该也清楚CORDIC算法来由啦。到这里,有同学又问了怎么Z不是0,最开始上面公式Z=0啊。简单来说,其实就是咱么在计算一个角度时,预设了一个角度φ,然后通过每次叠加与预设角度φ比对,来逼近预设角度,即Z=0的实质是
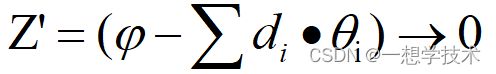
因此综合上述推导,整个CORDIC算法为
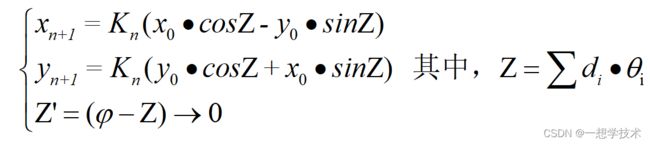
在实际应用中,往往是通过Z’参数来判断旋转符号。
其实,换一个角度理解,旋转公式
xn=x0 cosθ – y0 sinθ
yn= x0 sinθ + y0 cosθ
就是(x0,y0)圆坐标系一次性旋转θ,得到最终xn,yn。但是,回到前面开始说的圆坐标系旋转和伪旋转区别,其实就是相差一个伸缩因子Kn,现在已知迭代次数求得Kn,圆坐标系旋转乘以伸缩因子系数Kn,不就成伪旋转吗。只是表达式与前面叙述不一样,本质其实就是伪旋转。下面也给出迭代次数与伸缩因子关系表。
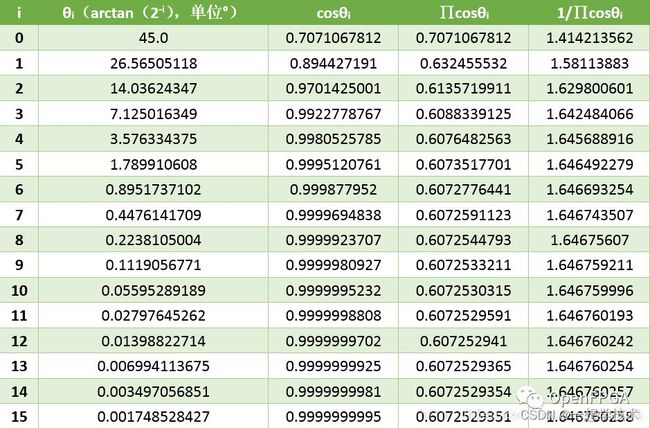
1.3 CORDIC算法操作模式
前面推导这么多,只是对CORDIC算法理论的推导,现在总算来到实际运用阶段啦。都知道CORDIC算法可以求三角函数,那么怎么求呢。实际上,CORDIC算法有两种操作模式,旋转模式和向量模式。前面推导的其实就是旋转模式
1.3.1旋转模式
简单看前面推导过程及结果,其实就明白,CORDIC算法的旋转模式可以求cosZ sinZ 。
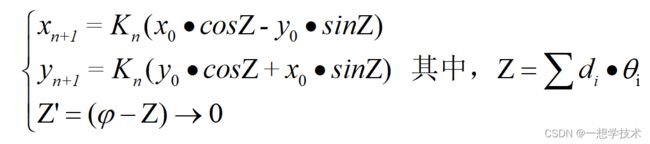
既然要求角度为Z的cosZ sinZ,那么根据上述公式,就可以设置初值,
x0 = 1/Kn 和 y0= 0 ,Z‘为判别条件,迭代后X值即为 cos z,y值即为 sin z
现附上旋转模式求解cosz, sinz的matlab程序,程序不难理解
close all;
clear;
clc;
% 初始化
die = 16;%迭代次数
x = zeros(die+1,1);
y = zeros(die+1,1);
z = zeros(die+1,1);
x(1) = 0.607253;%初始设置
z(1) = pi/3;%待求角度θ
%迭代操作
for i = 1:die
if z(i) >= 0%角度的符号判断
d = 1;
else
d = -1;
end
x(i+1) = x(i) - d*y(i)*(2^(-(i-1)));
y(i+1) = y(i) + d*x(i)*(2^(-(i-1)));
z(i+1) = z(i) - d*atan(2^(-(i-1)));%角度累加值
end
cosz = vpa(x(17),10)
sinz = vpa(y(17),10)
c = vpa(z(17),10)%最终累加角度误差值
求得,

FPGA的实现原理其实一样,主要注意角度的定点量化。量化位数直接影响计算精度,量化8位则一般迭代7次就结束,同时误差也会相对较大,如果量化32bit,则一般迭代16次就结束,误差相对较小。实际运用时平衡考虑FPGA资源以及误差。
先附上初值量化matlab程序
bit_quantify=32;
die=32;
%%初值
x0=0.607253;
y0=0;
Z0=pi/3;
theta=zeros(1,die);%以pi为基准量化
thetabin=zeros(1,die);
for i=1:1:die
theta(i)=atan(2^(-(i-1)));
end
%量化后的数据
xbin=dec2hex(round(x0/1*(2^(bit_quantify-1)-1)));
zbin=dec2hex(round(Z0/pi*(2^(bit_quantify-1)-1)));
for i=1:1:die
thetabin(i)=round(theta(i)/pi*(2^(bit_quantify-1)-1));
end
thetabin=dec2hex(thetabin);
直接附上FPGA实现代码,量化32bit进行计算
`timescale 1 ps/ 1 ps
module Cordic_Test
(
CLK_SYS,RST_N,
Phase,
Sin_out,Cos_out,Error
);
input CLK_SYS;
input RST_N;
input signed[31:0] Phase;//输入角度,弧度量化
output signed[31:0] Sin_out;
output signed[31:0] Cos_out;
output signed[31:0] Error;//角度误差
`define rot0 32'h20000000//45° 45°=pi/4=0.785398163397448 以pi为基准量化 pi/4*(2^31-1)
`define rot1 32'h12E4051D//26.5650511770780°
`define rot2 32'h09FB385B//14.0362434679265°
`define rot3 32'h051111D4//7.12501634890180°
`define rot4 32'h028B0D43//3.57633437499735°
`define rot5 32'h0145D7E1//1.78991060824607°
`define rot6 32'h00A2F61E//0.895173710211074°
`define rot7 32'h00517C55//0.447614170860553°
`define rot8 32'h0028BE53//0.223810500368538°
`define rot9 32'h00145F2F//0.111905677066207°
`define rot10 32'h000A2F98//0.0559528918938037°
`define rot11 32'h000517CC//0.0279764526170037°
`define rot12 32'h00028BE6//0.0139882271422650°
`define rot13 32'h000145F3//0.00699411367535292°
`define rot14 32'h0000A2FA//0.00349705685070401°
`define rot15 32'h0000517D//0.00174852842698045°
`define rot16 32'h000028BE//0.000874264213693780°
`define rot17 32'h0000145F//0.000437132106872335°
`define rot18 32'h00000A30//0.000218566053439348°
`define rot19 32'h00000518//0.000109283026720071°
`define rot20 32'h0000028C//5.46415133600854e-05°
`define rot21 32'h00000146//2.73207566800489e-05°
`define rot22 32'h000000A3//1.36603783400252e-05°
`define rot23 32'h00000051//6.83018917001272e-06°
`define rot24 32'h00000029//3.41509458500637e-06°
`define rot25 32'h00000014//1.70754729250319e-06°
`define rot26 32'h0000000A//8.53773646251594e-07°
`define rot27 32'h00000005//4.26886823125797e-07°
`define rot28 32'h00000003//2.13443411562898e-07°
`define rot29 32'h00000001//1.06721705781449e-07°
`define rot30 32'h00000001//5.33608528907246e-08°
`define rot31 32'h00000000//2.66804264453623e-08°
parameter Pipeline =16;//迭代次数
parameter Kn = 32'h4DBA775F; //K=0.607253*(2^31-1),32'h4DBA775F
reg signed [31:0] Sin;
reg signed [31:0] Cos;
reg signed [31:0] Error;
reg signed [31:0] reg_phase,phase_delay;
reg signed [31:0] xn [Pipeline:0];
reg signed [31:0] yn [Pipeline:0];
reg signed [31:0] zn [Pipeline:0];
reg signed [31:0] rot[Pipeline:0];
reg [1:0] Quadrant [Pipeline:0];
reg signed [31:0]overeult_xn,overeult_yn;
//-----------存储角度值-----------------------------
always @ (posedge CLK_SYS or negedge RST_N)
begin
if(!RST_N)
begin
rot[0] <= 1'b0;
rot[1] <= 1'b0;
rot[2] <= 1'b0;
rot[3] <= 1'b0;
rot[4] <= 1'b0;
rot[5] <= 1'b0;
rot[6] <= 1'b0;
rot[7] <= 1'b0;
rot[8] <= 1'b0;
rot[9] <= 1'b0;
rot[10] <= 1'b0;
rot[11] <= 1'b0;
rot[12] <= 1'b0;
rot[13] <= 1'b0;
rot[14] <= 1'b0;
rot[15] <= 1'b0;
rot[16] <= 1'b0;
end
else
begin
rot[0] <= `rot0;
rot[1] <= `rot1;
rot[2] <= `rot2;
rot[3] <= `rot3;
rot[4] <= `rot4;
rot[5] <= `rot5;
rot[6] <= `rot6;
rot[7] <= `rot7;
rot[8] <= `rot8;
rot[9] <= `rot9;
rot[10] <= `rot10;
rot[11] <= `rot11;
rot[12] <= `rot12;
rot[13] <= `rot13;
rot[14] <= `rot14;
rot[15] <= `rot15;
rot[16] <= `rot16;
end
end
//----------将要计算的角度转换到-pi/2到pi/2之间----------
always @(posedge CLK_SYS or negedge RST_N)
begin
if(!RST_N)
begin
reg_phase <= 0;
phase_delay <= 0;
end
else begin
phase_delay<= Phase;
case(Phase[31:30])//根据角度象限,将角度转换到可求区域
2'b00: reg_phase <= Phase;
2'b01: reg_phase <= Phase - 32'h3FFFFFFF; //-pi/2
2'b10: reg_phase <= Phase - 32'h7FFFFFFF; //-pi h7FFFFFFF
2'b11: reg_phase <= Phase - 32'hBFFFFFFF; //-3pi/2 hBFFFFFFF
default:reg_phase <= 32'h00;
endcase
end
end
//-------------迭代计算-----------
always @ (posedge CLK_SYS or negedge RST_N)
begin
if(!RST_N)
begin
xn[0] <= 32'h0;
yn[0] <= 32'h0;
zn[0] <= 32'h0;
end
else
begin
xn[0] <= Kn;
yn[0] <= 32'd0;
zn[0] <= reg_phase;
end
end
genvar die;
generate
for (die = 0; die >>die);
yn[die+1] <= yn[die] + (xn[die]>>>die);
zn[die+1] <= zn[die] - rot[die];
end
else begin
xn[die+1] <= xn[die] + (yn[die]>>>die);
yn[die+1] <= yn[die] - (xn[die]>>>die);
zn[die+1] <= zn[die] + rot[die];
end
end
end
endgenerate
//------根据实际角度输出结果--------------
genvar dif;
generate
for (dif = 0; dif 以pi/3为例,pi/3量化后相位为32‘h‘2AAAAAAA’ ,计算仿真结果如下
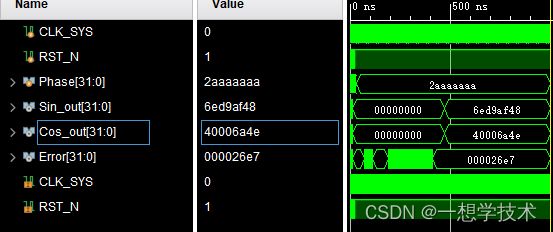
可知计算的cos(pi/3)=32’h40006a4e sin(pi/3)=32’h6ed9af48 计算结果都是量化后的结果,返回量化前的值如下

可知cos(pi/3)=0.5 sin(pi/3)=0.866,计算结果也是符号要求。例子中注意角度量化和数值量化的标准。
1.3.1向量模式
CORDIC算法还有一种模式是向量模式,直接附上公式

这又是个啥,怎么理解。别急,咱们回到前面推导过程中说过一句话,圆坐标系旋转和伪旋转区别,其实就是相差一个伸缩因子Kn
那么如果初值(x0,y0)不是在x轴上,是任意一个点,经过n次迭代后,yn逐渐旋转到X轴上,及yn=0,那么模值sqrt((x0^2 )+ ( y0 ^2))前乘上伸缩因子Kn即为伪旋转后Xn坐标也是模值,Zn即为旋转的角度值。
从式子中,可以看出,通过**设定初值z0=0,可以求(x0,y0)的夹角,**也即角度值Z。
借鉴网上的matlab程序如下,计算角度值
close all;
clear;
clc;
% 初始化
die = 16;%迭代次数
x = zeros(die+1,1);
y = zeros(die+1,1);
z = zeros(die+1,1);
x(1) = 100;%初始设置
y(1) = 200;%初始设置
k = 0.607253;%初始设置
%迭代操作
for i = 1:die
if y(i) >= 0
d = -1;
else
d = 1;
end
x(i+1) = x(i) - d*y(i)*(2^(-(i-1)));
y(i+1) = y(i) + d*x(i)*(2^(-(i-1)));
z(i+1) = z(i) - d*atan(2^(-(i-1)));
end
d = vpa(x(17)*k,10)
a = vpa(y(17),10)
c = vpa(rad2deg(z(17)),10)
由于本人实际开发过程中,利用FPGA计算角度值的地方运用较少,因此未进行FPGA的实现,感兴趣的同学可以根据matlab程序进行FPGA程序的移植。移植过程注意数值与角度的量化标准。
2、CORDIC算法总结
借鉴多个参考资料,根据本人对CORDIC算法实际运用和理解,总结下来CORDIC算法就4点:
(1)CORDIC算法就是通过伪旋转来简化计算,期间需要注意与圆坐标系旋转之间的关系。
(2)旋转模式就是从X轴上一点,伪旋转到某个角度的坐标点的过程,该模式下可计算cosz和sinZ。
(3)向量模式就是从某个角度的坐标点伪旋转到X轴上一点的过程,该模式下可计算角度值。两个模式的旋转恰好相反
(4)FPGA的实现时注意数值与角度的量化标准
(5)目前只介绍了圆坐标系的CORDIC算法,延伸到线性坐标系或双曲线坐标系,都可以推导以及实现三角函数计算