《啊哈！算法》知识点记录1 （1-3章（排序 队列 栈 枚举））

断断续续看了10天左右的时间，总的来说，这本书作为算法入门还是不错的，比较细致的讲解了一些基础的算法。今天终于不用做实验了，把知识点总结一下。

第1章 排序

要注意的是，这章的所有排序的数组arr[ ]作者都是默认从arr[ 1 ]开始的，实际上一般是从arr[0]开始

介绍了三种排序法，简化版的桶排序，冒泡排序，快速排序。
简化版的桶排的思想是：对于要排序的数字的数量，设置相应长度的一个数组。
比如如果需要对0~1000的整数进行排序，就需要长度为1001的数组记录每个数出现的次数。
从大到小排序核心代码如下

	for (i = 1;i <= n;i++)//循环读入n个数，并进行桶排序
	{
		scanf_s("%d", &t);
		book[t]++;//标记
	}
	for (i = 1000;i >= 0;i--)//从大到小输出
		for (j = 1;j <= book[i];j++)
			printf("%d", i);

如果将桶的个数记为m,待排序个数为n的话，桶排序的时间复杂度为O（M+N）

冒泡排序的思想为：每次比较两个相邻的元素，如果它们的顺序错误就把它们交换过来，如果有n个数，需要将n-1个数进行归位。
从大到小排序核心代码如下

for (i = 1;i < =n - 1;i++)//n个数排序，只需要进行n-1轮
	{
		for (j = 1;j <= n - i;j++)//从第1位开始，进行比较，每完成一个数的排序，下一个数所需要排序的次数就递减
		{
			if (arr[j] < arr[j + 1])
			{
				t = arr[j];
				arr[j] = arr[j + 1];
				arr[j + 1] = t;
			}
		}
    }

冒泡排序的时间复杂度为O(N^2)

快速排序的思想：类似于“二分法”，按从小到大排序方法是首先找到一个基准数，然后将序列中所有比基准数大的放在其右边，比基准数小的放在其左边。每一轮处理其实就是讲这一轮的基准数归位，直到所有的数归位。
从小到大排序的核心代码如下：

void quicksort(int left,int right)
{
    int i,j,t,temp;
    if(left>right)
        return;
    temp=a[left]; //temp中存的就是基准数
    i=left;
    j=right;
    while(i!=j)
    {
        //顺序很重要，要先从右往左找
        while(a[j]>=temp && i<j)
            j--;
        //再从左往右找
        while(a[i]<=temp && i<j)
            i++;
        //交换两个数在数组中的位置
        if(i<j)//当哨兵i和哨兵j没有相遇时
        {
            t=a[i];
            a[i]=a[j];
            a[j]=t;
        }
    }
    //最终将基准数归位
    a[left]=a[i];
    a[i]=temp;
    quicksort(left,i-1);//继续处理左边的，这里是一个递归的过程
    quicksort(i+1,right);//继续处理右边的，这里是一个递归的过程
}

注意，要先从右往左进行寻找，因为设置的基准数是在最左边，所以要从基准数的对面先开始。
比如随便一个队列5 3 4 7 8 6 9，第一轮的基准数为5，如果先从右边开始，j先动，则j会在4停下来，i会在3停下，然后交换，这时为5 4 3 7 8 6 9，这时,j指向的数为3，i为4，接下来继续判定，j不动，i移动到3，然后j=i,交换基准数.这时队列变成了3 4 5 7 8 6 9. 第一轮快速排序结束。

如果是从左边先开始的话.假设队列初始化为5 3 4 7 8 6 9,i先动，i会移动到7这个位置，然后j开始移动，j移动到7时，这时i=j,会直接进行交换.这时队列变成了7 3 4 5 8 6 9很明显是错误的。
快速排序的最差时间复杂度为O(N^2）,平均时间复杂度为O(NlogN)
.
.
.

三种排序方法：桶排序最快，如果将桶的个数记为m,待排序个数为n的话，桶排序的时间复杂度为O（M+N），冒泡排序的时间复杂度为O(N^2)，快速排序的平均时间复杂度为O(NlogN)

**

第二章 栈 队列 链表

本章中纸牌游戏的代码似乎有一点问题，我运行的结果与书中答案不一致

**

队列有三个基本元素：一个数组（用来存储内容），2个变量（用来标记队首和队尾）
它是一种特殊的线性结构，只允许在队列的首部（head）进行删除操作，这成为“出队”，而在队列的尾部（tail）进行插入操作，称为“入队”。服从“先进先出”的原则。
.
.

注意：队尾的标记指向队列的最后一位的下一个位置
书中用一个题目来介绍了队列
给出的队列为6 3 1 7 5 8 9 2 4
将序列的第一个数删除，将第二个数移到序列末尾；
将序列的第三个数删除，将第四个数移到序列末尾；
将序列的第五个数删除，将第六个数移到序列末尾
.
.
直到剩下最后一个数，将最后一个数也删除。
核心代码如下：

//当头标记小于尾标记时
while(head<tail){
printf("%d,",q[head]);  //打印被删除出列的数据
head++;            //然后进行真正的删除操作

q[tail] = q[head];  //先将新队首的数添加到队尾
tail++;  //尾标记后移
head++; //头标记移到下一个待处理的数据
}

删除的顺序为：6 1 5 9 4 7 2 8 3

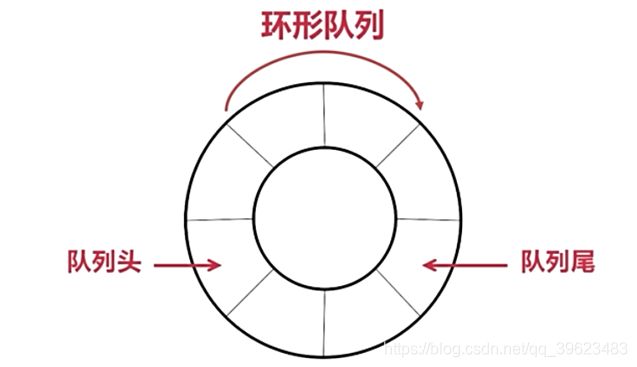
本书没有介绍环形队列，所以在这里附上一个博主关于环形队列的阐述，感觉很清晰，有兴趣的朋友可以看这篇文章来理解环形队列。

栈：和队列不同，它是“后进先出”，限定为只能在一端进行插入和删除操作

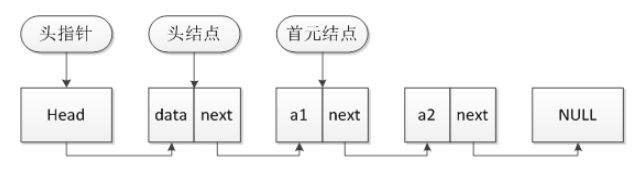
链表：可以动态的进行存储分配，可以根据需要随意增添，删除，插入节点，主要运用的是结构体指针链表中的每一个介节点都由两部分组成，一部分用于存储数据，一部分用来存储下一个节点的地址。一般这样定义：

struct node
{
	int data;//用于存放数据
	struct  node* next;//存储下一个节点的地址
};

本书主要讲述了单向链表

书中源码如下所示，没有使用free函数去释放动态申请的空间

#include  
#include  
//这里创建一个结构体用来表示链表的结点类型
struct node 
{ 
 int data; 
 struct node *next; 
}; 
int main() 
{ 
 struct node *head,*p,*q,*t; 
 int i,n,a; 
 scanf("%d",&n); 
 head = NULL;//头指针初始为空
 for(i=1;i<=n;i++)//循环读入n个数
 { 
 scanf("%d",&a); 
 //动态申请一个空间，用来存放一个结点，并用临时指针p指向这个结点
 p=(struct node *)malloc(sizeof(struct node)); 
 p->data=a;//将数据存储到当前结点的data域中
 p->next=NULL;//设置当前结点的后继指针指向空，也就是当前结点的下一个结点为空
 if(head==NULL) 
 head=p;//如果这是第一个创建的结点，则将头指针指向这个结点
 else 
 q->next=p;//如果不是第一个创建的结点，则将上一个结点的后继指针指向当前结点
 q=p;//指针q也指向当前结点
 } 
 //输出链表中的所有数
 t=head; 
 while(t!=NULL) 
 {
  printf("%d ",t->data); 
 t=t->next;//继续下一个结点
 }  
 return 0; 
}

关于双向链表和循环链表等知识点，可以查阅Tupac.Amaru.Shakur的博文
还有zql_3393089的这篇博文也很详细的讲述了链表

第三章 枚举

枚举的基本思想为：有序地去尝试每一种可能
例子：写出123的全排列

for (a = 1; a <= 3; a++) {
		for (b = 1; b <= 3; b++) {
			for (c = 1; c <= 3; c++) {
				if (a != b && a != c && b != c)
					printf("%d%d%d\n",a,b,c)