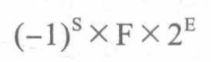计算机中浮点数表示

• 浮点数表示

浮点数在计算机中由符号位、指数和尾数组合而成。

通常，浮点数表示为如下形式：

F为小数(尾数)字段值，E为指数字段值。

溢出(浮点的上溢)：正的指数太大而超过了指数字段的表示范围。

下溢：负的指数太大而超过了指数字段的表示范围。

减少溢出方法

在c语言中称为double，基于double的操作称为双精度(double precision)浮点运算。

• IEEE 754浮点标准

IEEE 754隐藏了规格化二进制小数点前面的1.因此，在单精度下，数据有24位(隐含的1和23位尾数)，在双精度下为53位(1+52)。为了精确， 用术语有效位(sigificand)来表示24位或者53位的数，即隐含的1加上尾数，尾数为23或者52位。因为0没有前导位1，其指数保留为0，所以硬件不会将1加到尾数前面。

其中，尾数代表一个0和1之间的数，E指明了指数字段的值。如果从左到右将尾数各位标记为s1,s2,s3,...,则数的值为：

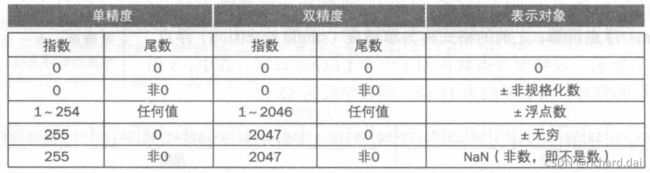
IEEE 754标准特殊符号表示

IEEE 754给出了一个符号用以表示无效操作的结果，如0/0或者无穷减无穷。该符号位NaN,意为非数(Not a Number)。使用NaN的目的是让程序员推迟程序中的一些测试和决断。

• 为什么浮点数的符号位放在最高位？

原因是符号位放在最高有效位便于快速测试大于、小于、等于0的情况。

同理，将指数放在有效位前也能够简化使用证书比较直立来实现的浮点数排序，因为在两个指数的符号相同的情况下，具有较大指数的数看起来要比指数较小的数大。

• 负的指数挑战

符的指数对简化排序造成了挑战。如果我们用补码或者其他的计数法，可能会使负指数中指数字段的最高位为1，从而使负指数看上去是一个很大的数，例如，1.0*2^-1以单精度表示为：

注意，有效位前面还有一个隐含的1，而数1*2^+1看似是一个较小的二进制数。

我们希望计数法能将最小的负指数(绝对值最大的负指数)表示为000...000（二进制）,而最大的正指数表示为111...111（二进制）。这种约定称为移码表示，从正常的树中减去一个无符号的偏差值，从而获得真实的值。

    IEEE 754规定单精度的偏差为127,因此指数-1表示为-1+127(十进制)的二进制形式，即126(十进制) = 01111110(二进制)，即128 = 10000000(二进制)。双精度的指数偏差为1023。带偏差的指数意味辙浮点数表示的值实际为:

(-1)^S * (1 + 尾数) * 2^(指数-偏差)

从而，单精度的表示范围从± 1.000000000000000000000(二进制) * 2^(-126) 到 ±111111111111111111111(二进制)* 2^(+127)

注意指数为0以及指数最大有特殊含义。