【算法】换根DP

什么是换根DP

https://oi-wiki.org/dp/tree/#%E6%8D%A2%E6%A0%B9-dp

树形 DP 中的换根 DP 问题又被称为二次扫描，通常不会指定根结点，并且根结点的变化会对一些值，例如子结点深度和、点权和等产生影响。

通常需要两次 DFS，第一次 DFS 预处理诸如深度，点权和之类的信息，在第二次 DFS 开始运行换根动态规划。

例题分析——P3478 [POI2008] STA-Station

https://www.luogu.com.cn/problem/P3478

题目列表1

834. 树中距离之和⭐⭐⭐⭐⭐（两次 dfs）

834. 树中距离之和

思路——冷静分析，列出式子

https://leetcode.cn/problems/sum-of-distances-in-tree/solutions/103325/c-liang-ci-dfsde-dao-da-an-by-congwang357-2/

将问题拆分：对于两个相邻节点A和B，将树拆分为两个子树，根节点分别为A和B，A节点到其他所有节点的距离和 ans(A) = A子树中所有节点到A节点的距离和sum(A) + B子树中所有节点到B节点的距离和sum(B) + B子树的大小cnt(B);
同理，ans(B) = sum(B) + sum(A) + cnt(A);

由此我们得到： ans(A) = sum(A) + sum(B) + cnt(B); ans(B) = sum(B) + sum(A) + cnt(A);
则，两个相邻接点的解之间的关系为：ans(A) = ans(B) - cnt(A) + cnt(B) = ans(B) - cnt(A) + (N - cnt(A));

因此，对于根节点root的任意子节点child，ans(child) = ans(root) - cnt(child) + N - cnt(child);

class Solution {
    List<Integer>[] g;
    int[] ans, size;    // size是各个节点作为根节点的子树大小
    int n;
    public int[] sumOfDistancesInTree(int n, int[][] edges) {
        g = new ArrayList[n];
        Arrays.setAll(g, e -> new ArrayList<Integer>());
        for (int[] edge: edges) {
            int x = edge[0], y = edge[1];
            g[x].add(y);
            g[y].add(x);
        }
        this.n = n;
        ans = new int[n];
        size = new int[n];
        Arrays.fill(size, 1);

        dfs(0, -1, 0);
        reroot(0, -1);
        return ans;
    }

    // 求ans[0]和各个size[i]
    void dfs(int x, int fa, int depth) {
        ans[0] += depth;                    // depth 是 0 到 x 的距离
        for (int y: g[x]) {
            if (y != fa) {
                dfs(y, x, depth + 1);
                size[x] += size[y];         // 累加 x 的儿子 y 的子树大小
            }
        }
    }

    // 求答案
    void reroot(int x, int fa) {
        for (int y: g[x]) {
            if (y != fa) {
                ans[y] = ans[x] + n - 2 * size[y];
                reroot(y, x);
            }
        }
    }
}

算法分析⭐⭐⭐⭐⭐

https://leetcode.cn/problems/sum-of-distances-in-tree/solutions/2345592/tu-jie-yi-zhang-tu-miao-dong-huan-gen-dp-6bgb/

我们得到了重要公式：
$ans[y]=ans[x]+n-2\ast size[y]$

如何理解？
y 和以 y为根的子树的距离相比 x 与 以 y为根的子树的距离 少了 cnt[y]
除了 以 y为根的子树，剩下的节点数量是 n - cnt[y]，这些和 y 的距离相比 和 x 的距离多了 n - cnt[y]

因此：ans[y] = ans[x] + n - 2 * size[y]

310. 最小高度树⭐⭐⭐⭐⭐

https://leetcode.cn/problems/minimum-height-trees/description/

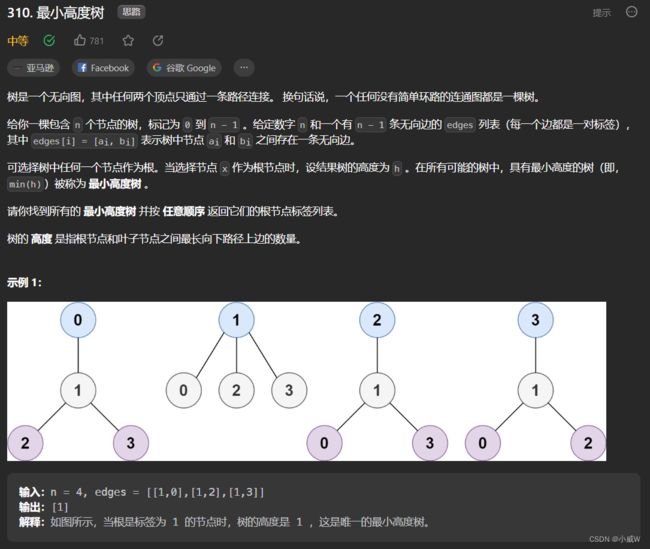
提示：

1 <= n <= 2 * 10^4
edges.length == n - 1
0 <= ai, bi < n
ai != bi
所有 (ai, bi) 互不相同
给定的输入 保证 是一棵树，并且 不会有重复的边

主要参考 ：https://leetcode.cn/problems/minimum-height-trees/solutions/1397830/c-huan-gen-by-vclip-sa84/ 编写的代码。

class Solution {
    List<Integer> ans = new ArrayList<Integer>();
    List<Integer>[] g;
    int n;
    int[] ds, ds2;

    public List<Integer> findMinHeightTrees(int n, int[][] edges) {
        this.n = n;
        ds = new int[n];
        ds2 = new int[n];
        // 建树
        g = new ArrayList[n];
        Arrays.setAll(g, e -> new ArrayList());
        for (int[] edge: edges) {
            int x = edge[0], y = edge[1];
            g[x].add(y);
            g[y].add(x);
        }

        dfs(0, -1);     // 求各个节点为根的子树高度（以0节点为最根节点）
        dfs2(0, -1);    // 换根dp

        // 求答案
        int h = n;
        for (int i = 0; i < n; ++i) {
            if (ds2[i] < h) {
                h = ds2[i];
                ans.clear();
            }
            if (ds2[i] == h) ans.add(i);
        }
        return ans;
    }

    // 计算以0号节点为根的树中，以各个节点为根的子树高
    public int dfs(int x, int fa) {
        for (int y: g[x]) {
            if (y != fa) {
                ds[x] = Math.max(ds[x], dfs(y, x) + 1);
            }
        }
        return ds[x];
    }

    // 进行换根动态规划，计算出所有的树高
    public void dfs2(int x, int fa) {
        // 计算 x 的子树高的最大值和次大值
        int first = -1, second = -1;    // 默认是没有子树
        for (int y: g[x]) {
            if (ds[y] > first) {
                second = first;
                first = ds[y];
            } else if (ds[y] > second) second = ds[y];
        }
        ds2[x] = first + 1;             // 计算出 x 为根的树高
        // 进行换根，计算x作为以y为根节点的树的子树时的高度
        for (int y: g[x]) {             
            if (y != fa) {
                ds[x] = (ds[y] != first? first: second) + 1;
                dfs2(y, x);
            }
        }
    }
}

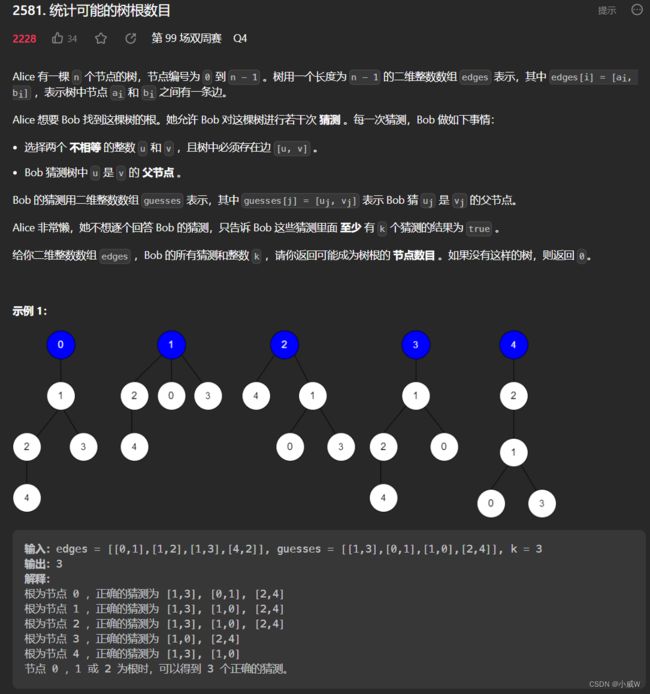
2581. 统计可能的树根数目⭐⭐⭐⭐⭐

https://leetcode.cn/problems/count-number-of-possible-root-nodes/

提示：

edges.length == n - 1
2 <= n <= 10^5
1 <= guesses.length <= 10^5
0 <= ai, bi, uj, vj <= n - 1
ai != bi
uj != vj
edges 表示一棵有效的树。
guesses[j] 是树中的一条边。
guesses 是唯一的。
0 <= k <= guesses.length

在这里插入代码片

C. Bear and Tree Jumps

https://codeforces.com/problemset/problem/771/C

在这里插入代码片

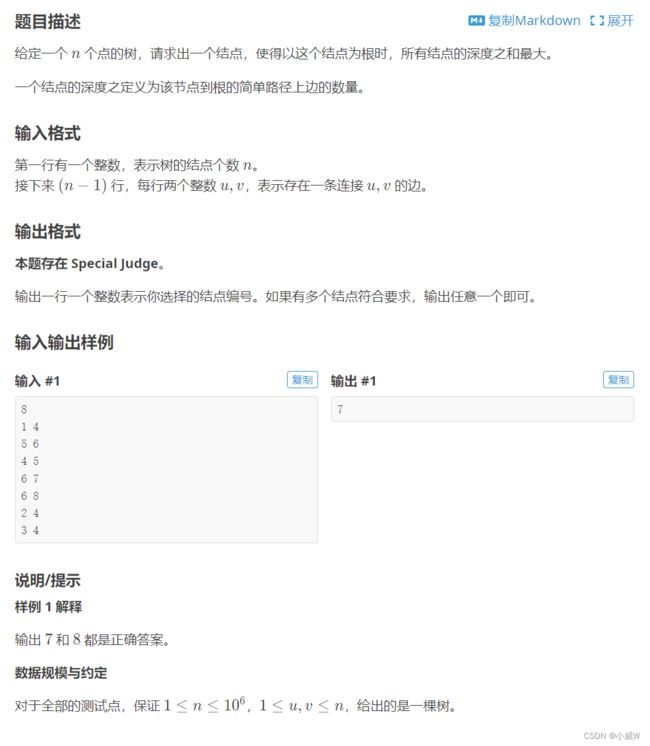
287. 积蓄程度

https://www.acwing.com/problem/content/289/

题目列表2

Atcoder Educational DP Contest, Problem V, Subtree

https://atcoder.jp/contests/dp/tasks/dp_v

Educational Codeforces Round 67, Problem E, Tree Painting

https://codeforces.com/contest/1187/problem/E

POJ 3585 Accumulation Degree

http://poj.org/problem?id=3585

[USACO10MAR]Great Cow Gathering G

https://www.luogu.com.cn/problem/P2986

CodeForce 708C Centroids

https://codeforces.com/problemset/problem/708/C

相关链接

关于基础树形DP可见：
【算法】树形DP ①（树的直径）
【算法】树形DP ② 打家劫舍Ⅲ（树上最大独立集）