双指针法总结

双指针法在对数组做出某种改变中经常用到，优点是时间复杂度为O(n)，且一般空间复杂度也比较低。

所谓双指针法，就是利用两个指针（不一定真是指针，能存储相应元素的位置就行）分别标识两个位置，然后通过指针所指元素的性质对数组进行修改，同时指针进行移动完成目标的方法。

一般双指针有两种使用方法，一是分为快慢指针，慢指针指向下一个要填充的位置，快指针指向下一个要判断的位置，若快指针指向的元素符合相应的条件，则把元素填充（或交换）到慢指针所指位置，然后两个指针进行移动。这样还可以保持数组的相对顺序（如果不用保持相对顺序其实有时候双指针还可以优化一点点，这里就不讲了）。

二就是分为普通的两个指针，指向左边右边，然后比较两个指针所指元素看哪个元素符合条件再把相应元素移动到对应容器位置中，指针进行移动，不过这种情况要注意一下边界的判断。

手动分割--------------------------------------------------------------------------------

上面的是之前的想法，后面我发现双指针博大精深啊，又添加了两道链表的题，双指针可以解决一遍遍历解决不了的事情，毕竟有两个指针嘛，还可以解决追及相遇问题，即两个指针以不同的初始位置或不同的速度前进后相遇了代表什么。
所以现在双指针有四种用法：

1. 用快指针指向的符合条件的数据填充慢指针指向的位置；
2. 两个指针指向的元素互相比较，选出符合条件的元素填入指定容器；
3. 解决一遍遍历解决不了但两遍或多次遍历能解决的问题；
4. 通过快慢指针的移动以及两者的相遇选出特定条件。

接下来看具体的题

第一题

这个就是个典型的双指针问题，慢指针指向下一个要填充的位置，快指针指向要判断的元素，如果快指针指向元素不等于val，就填充到慢指针所指位置，否则快指针继续判断下一个元素。

class Solution {
public:
    int removeElement(vector<int>& nums, int val) {
        int left = 0;
        int n = nums.size();
        for (int right = 0; right < n; right++) {
            if (nums[right] != val) {
                nums[left] = nums[right];
                left++;
            }
        }
        return left;
    }
};

其实这道题怎么写LeetCode都给过，暴力求解也行，下面还写了一种用排序来做的算法，没啥大用

/**
 * 解题思路：先对数组排序，然后从头和从尾找到要移除的元素的位置记录，然后计算出剩余数组的长度，
 * 利用循环把要移除的元素中在剩余长度的部分与尾部的元素交换。返回剩余长度值。
 * 
 */
class Solution {
public:
    int removeElement(vector<int>& nums, int val) {
        int result = 0;
        sort(nums.begin(), nums.end());
        int len = nums.size();
        int left = 0, right = len - 1;
        while (true) {
            if (nums[left] == val && nums[right] == val) 
                break;
            if (nums[left] != val) 
                left++;
            if (nums[right] != val)
                right--;
            if(left > right)
                return len;            
        }
        result = len - (right - left + 1); 
        for (int i = left; i < result; i++) {
            nums[i] = nums[++right];
        }
        return result;
    }
};

第二题

还是双指针，慢指针指向填充位置，快指针指向要判断的元素，若元素不等于前一个元素，说明是独特的元素，就填充过去。

class Solution {
public:
    int removeDuplicates(vector& nums) {
        int slow = 1;
        int n = nums.size();
        if (n == 0)
            return 0;
        for (int fast = 1; fast < n; fast++) {
            if (nums[fast] != nums[fast - 1]) {
                nums[slow] = nums[fast];
                slow++;
            }
        }
        return slow;
    }
};

第三题

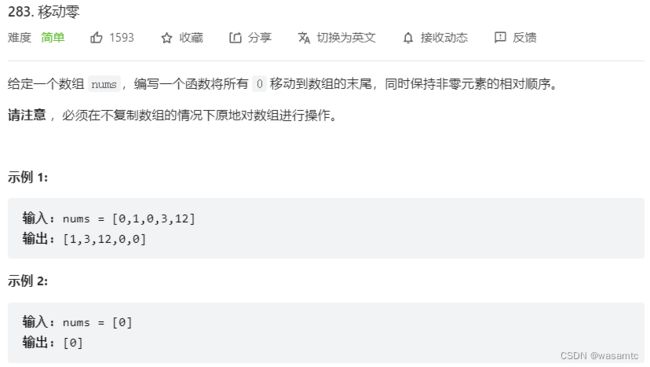
这题就不说了，可能是最简单的一道题。

class Solution {
public:
    void moveZeroes(vector<int>& nums) {
        int slow = 0;
        int n = nums.size();
        for (int fast = 0; fast < n; fast++) {
            if (nums[fast] != 0) {
                int temp = nums[slow];
                nums[slow] = nums[fast];
                nums[fast] = temp;
                slow++;
            }
        }
    }
};

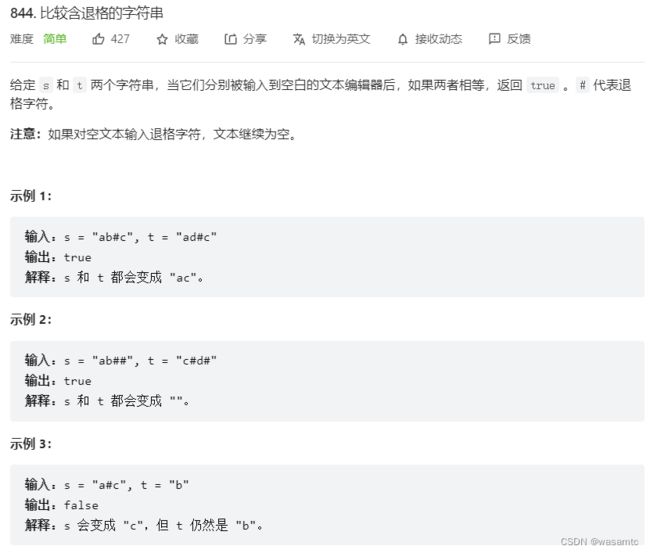
第四题

这题也比较简单，就慢指针指向填充位置，快指针指向的若是字母就填充，若不是则慢指针填充位置减1，相当于删去了一个元素，只不过要注意慢指针退到边界后就不用再退了。

class Solution {
public:
    bool backspaceCompare(string s, string t) {
        int slow1 = 0, slow2 = 0;
        int len1 = s.length(), len2 = t.length();
        for (int fast = 0; fast < len1; fast++) {
            if (s[fast] != '#') {
                s[slow1] = s[fast];
                slow1++;
            }
            else if (slow1 != 0) {
                slow1--;
            }
        }
        for (int fast = 0; fast < len2; fast++) {
            if (t[fast] != '#') {
                t[slow2] = t[fast];
                slow2++;
            }
            else if (slow2 != 0) {
                slow2--;
            }
        }
        if (slow1 != slow2)
            return false;
        for (int i = 0; i < slow1; i++) {
            if (s[i] != t[i])
                return false;
        }
        return true;
    }
};

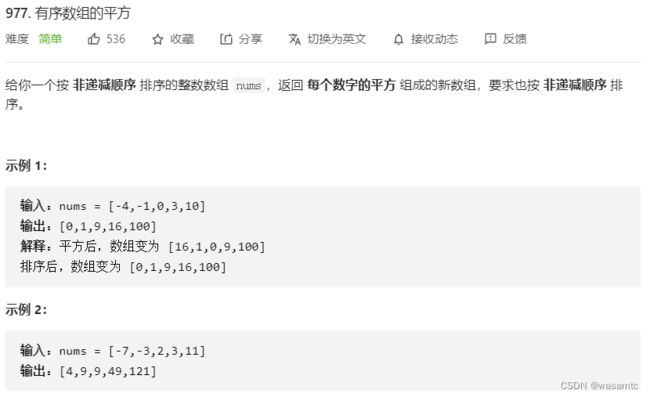
第五题

这个就不属于快慢指针了，属于左右指针的元素比较，最重要的（而且很明显的）要找到正负数的交界线，然后互相比较。

**
 * 解题思路：用双指针法，左指针指向负数，右指针指向正数，先通过循环使得两个指针分别指向最后一个负数和第一个正数
 * 如果都是正数指针分别为-1,0；如果都是负数指针分别为len-1，len,。设定一个结果数组。开始循环，循环终止条件为左指针小于0
 * 且右指针大于等于len。如果左指针大于等于0且右指针小于len，则将两个元素中较小者填入结果数组中，同时相应指针移动。
 * 如果左指针小于0，将右指针所指内容填入结果，移动右指针，如果右指针大于等于len，将左指针所指内容填入结果，移动左指针。
 * 返回结果数组。(上面应该是将内容的平方填入结果数组)
 * 
 */
class Solution {
public:
    vector<int> sortedSquares(vector<int>& nums) {
        vector<int> result;
        int len = nums.size();
        int left = -1, right = len;
        for (int i = 0; i < len - 1; i++) {
            if (nums[i] < 0 && nums[i + 1] >= 0) {
                left = i;
                right = i + 1;
                break;
            }
        }
        if (left == -1 && nums[0] < 0) 
            left = len - 1;
        else if (left == -1 && nums[0] >= 0)
            right = 0;
        while (left >= 0 || right < len) {
            if (left >= 0 && right < len) {
                int temp;
                if (abs(nums[left]) <= abs(nums[right])) {
                    result.push_back(nums[left] * nums[left]);
                    left--;
                }
                else {
                    result.push_back(nums[right] * nums[right]);
                    right++;
                }
            }
            else if (left < 0) {
                result.push_back(nums[right] * nums[right]);
                right++;
            }
            else if (right >= len) {
                result.push_back(nums[left] * nums[left]);
                left--;
            }
        }
        return result;
    }
};

第六题

19. 删除链表的倒数第 N 个结点

这道题其实我最初做有那么一点点双指针的想法，不过我那双指针是每次移动到一个节点后从这个节点往前走n步，可以一开始就设置两个指针，一个在开头，另一个开头n步的地方，然后走。

/**
 * 解题思路：使用双指针，一个指向当前节点，一个从当前节点走n步，如果走到nullptr，说明当前节点就是倒数第n
 * 个节点，则删除该节点并返回头结点，为了删除该节点，每次我们还要保留当前节点的前一个节点，设立一个空头结点。
 */
class Solution {
public:
    ListNode* removeNthFromEnd(ListNode* head, int n) {
        ListNode *emptyHead = new ListNode(0, head);
        ListNode *slow = head;
        ListNode *fast = slow;
        ListNode *prev = emptyHead;
        for (int i = 0; i < n; i++)
            fast = fast->next;
        while (true) {
            if (fast == nullptr) {
                prev->next = slow->next;
                return emptyHead->next;
            }
            prev = slow;
            slow = slow->next;
            fast = fast->next;
        }
    }
};

第七题

面试题 02.07. 链表相交

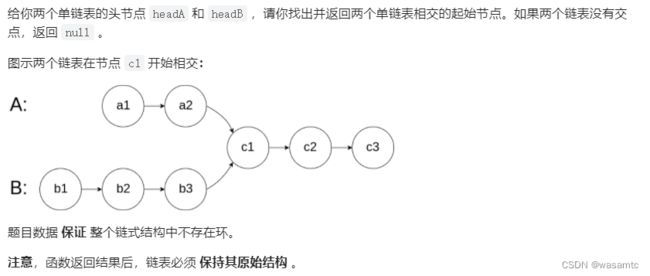
这道题当然很容易想到哈希表，毕竟哈希表很适合拿来比较有没有相同的，快慢指针比较难想到，主要快慢指针在这里属于追及相遇，需要仔细思考一下快指针和慢指针怎么走才能让相遇的时候可以求出相交节点，这种一般要仔细思考快慢指针分别走过的距离以及关系。

/**
 * 解题思路：双指针法，一个指针指向a的开头，一个指针指向b的开头，两个指针同时开始前行，如果两个指针所指一样，
 * 则返回任何一个，如果其中某个为null，则跳转到另一个表的开头去。为什么双指针法可以，因为无论怎样，用这种方法最后
 * 两个指针走过的距离一样，如果有相交的，一定能找出来。
 */
class Solution {
public:
    ListNode *getIntersectionNode(ListNode *headA, ListNode *headB) {
        ListNode *nodeA = headA;
        ListNode *nodeB = headB;
        while (nodeA != nullptr || nodeB != nullptr) {
            if (nodeA == nodeB)
                return nodeB;
            nodeA = (nodeA == nullptr ? headB : nodeA->next);
            nodeB = (nodeB == nullptr ? headA : nodeB->next);
        }
        return nullptr;
    }
};

第八题

142. 环形链表 II

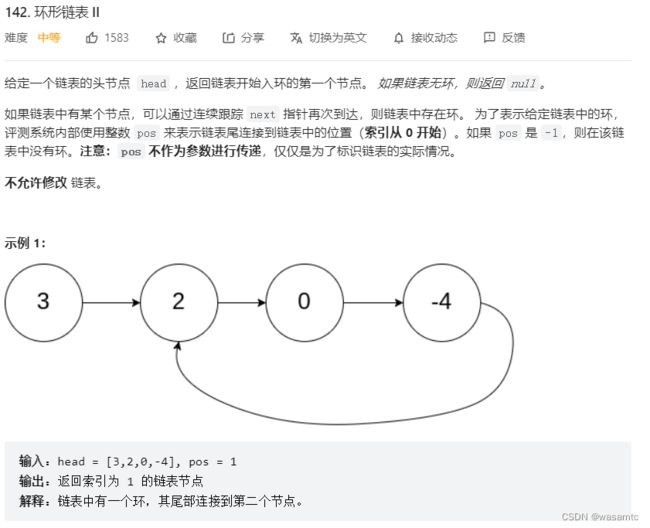
这道题用哈希表来做还是很简单，用双指针的话就要仔细思考两个指针的距离关系了，即如果慢指针走一步而快指针走两步的话两者一定会在慢指针走环的第一圈的时候相遇，为什么呢，想象快指针最难在第一圈追上慢指针的情况：慢指针刚进环，而快指针就比慢指针多了一步，此时两者相差距离最多（因为快指针离慢指针的距离为圈的距离减1），但即便是这种情况，当慢指针走完第一圈，快指针也走完了两圈，此时慢指针在原点，而快指针也在原点+1的位置，快指针一定在某个位置超过了慢指针！后面的计算看官方题解吧，反正相遇了还没完，所以比较麻烦。
这里只列哈希表的做法。

 /**
 * 解题思路：这道题用哈希表还是很容易想到的，但是用双指针怎么做我是真想不清楚，先用哈希表做吧
 */
class Solution {
public:
    ListNode *detectCycle(ListNode *head) {
        int index = 0;
        unordered_set<ListNode*> hadGO;
        while (head != nullptr) {
            if (hadGO.find(head) != hadGO.end())
                return head;
            hadGO.insert(head);
            head = head->next;
        }
        return NULL;
    }
};

总结

双指针法用于数组的改变，时间复杂度为O(n)，可以使用为快慢指针（判断填充）和左右指针（元素比较）。