医学图像分割评价指标
医学图像分割评价指标
- 1 引言
-
- 1.1 混淆矩阵 Confusion Matrix
- 2 what is TP,TN,FP,FN
- 3 PA 像素准确率
- 4 交并比 IOU
- 5 骰子系数 Dice
- 6 敏感度Sensitivity
- 7 阳性预测值 PPV
- 8 表面距离计算
-
- 8.1 **Hausdorff distance 豪斯多夫距离**
- 9 快速实现指标的工具和代码
1 引言
语义分割是像素级别的分类,其常用评价指标:
像素准确率(Pixel Accuracy,PA)
交并比(Intersection over Union,IoU)
Dice系数(Dice Coeffcient)
敏感度 (Sensitivity)
阳性预测值(Precision Predictive Value,PPV)
豪斯多夫距离 Hausdorff_95 (95% HD)
其计算都是建立在混淆矩阵(Confusion Matrix)的基础上。
1.1 混淆矩阵 Confusion Matrix
考虑一个二分类的情况,类别为1和0,我们将1和0分别作为正类(positive)和负类(negative),则实际分类的结果有4种,表格如下:

- TP: 真阳性数,在label中为阳性,在预测值中也为阳性的个数
- TN: 真阴性数, 在label中为阴性,在预测值中也为阴性的个数
- FP: 假阳性数, 在label中为阴性,在预测值中为阳性的个数
- FN: 假阴性数, 在label中为阳性,在预测值中为阴性的个数
**混淆矩阵(confusion matrix)**是以模型预测的类别数量统计信息为横轴,真实标签的数量统计信息为纵轴画出的矩阵。
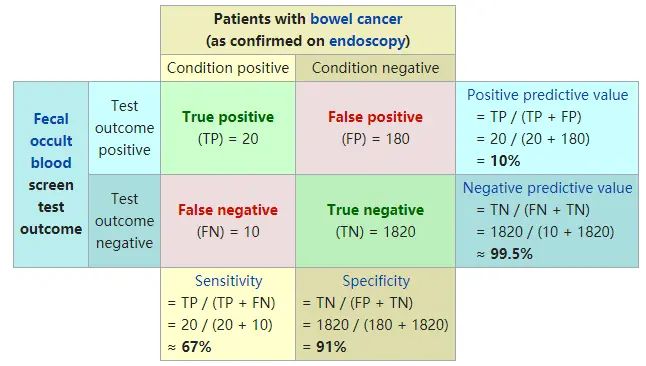
从这个表格中可以引出一些其它的评价指标:
- ACC:classification accuracy,描述分类器的分类准确率
计算公式为:ACC=(TP+TN)/(TP+FP+FN+TN) - BER:balanced error rate
计算公式为:BER=1/2*(FPR+FN/(FN+TP)) - TPR:true positive rate,描述识别出的所有正例占所有正例的比例
计算公式为:TPR=TP/ (TP+ FN) - FPR:false positive rate,描述将负例识别为正例的情况占所有负例的比例
计算公式为:FPR= FP / (FP + TN) - TNR:true negative rate,描述识别出的负例占所有负例的比例
计算公式为:TNR= TN / (FP + TN) - PPV:Positive predictive value
计算公式为:PPV=TP / (TP + FP) - NPV:Negative predictive value
计算公式:NPV=TN / (FN + TN)
其中TPR即为敏感度(sensitivity),TNR即为特异度(specificity)
2 what is TP,TN,FP,FN
TP:True Positive,被判定为正样本,事实上也是正样本 ,即蓝色与红色的交集:

**TN:True Negative,**被判定为负样本,事实上也是负样本,即红色与蓝色以外区域

FP:False Positive,被判定为正样本,但事实上是负样本,即红色中除了蓝色部分

**FN:False Negative,**被判定为负样本,但事实上是正样本,即蓝色中除了红色部分
3 PA 像素准确率
定义: 它是图像中正确分类的像素百分比。即分类正确的像素占总像素的比例。用公式可表示为:
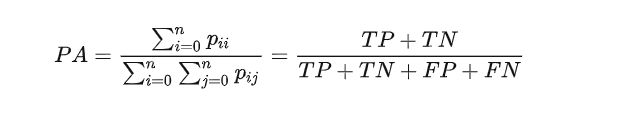
TP+TN+FP+FN=总像素数 TP+TN=正确分类的像素数
因此,PA 可以用两种方式来计算。
下面使用一个3 * 3 简单地例子来说明: 下图中TP=3,TN=4, FN=2, FP=0


即图中正确分类的像素数为7,总像素数为9。
代码表达:
def binary_pa(s, g):
"""
calculate the pixel accuracy of two N-d volumes.
s: the segmentation volume of numpy array
g: the ground truth volume of numpy array
"""
pa = ((s g).sum()) / g.size
return pa
g = np.array([1, 1, 1, 1, 1, 0, 0, 0, 0])
s = np.array([0, 1, 0, 1, 1, 0, 0, 0, 0])
pa = binary_pa(s, g)
注:思考一下,PA很简单,但是,它绝不是最好的指标,因为分割任务存在的类别不平衡问题。解释如下:

在这个案例中,即使模型什么也没有分割出来,但他的PA = 95%, what???
嗯。我们的计算有问题吗?不。完全正确。只是背景类是原始图像的 95%。因此,如果模型将所有像素分类为该类,则 95% 的像素被准确分类,而其他 5% 则没有。
因此,尽管您的准确率高达 95%,但您的模型返回的是完全无用的预测。这是为了说明高像素精度并不总是意味着卓越的分割能力。
这个问题称为类别不平衡。当我们的类极度不平衡时,这意味着一个或一些类在图像中占主导地位,而其他一些类只占图像的一小部分。不幸的是,类不平衡在许多现实世界的数据集中普遍存在,因此不容忽视。
因此,这个指标基本没什么指导意义。
其中,为了解决类别不平衡问题,提出了一些像素准确率的改进方案:如CPA,MPA
CPA:类别像素准确率
对应:精准率(Precision)
含义:在类别 i 的预测值中,真实属于 i 类的像素准确率,换言之:模型对类别 i 的预测值有很多,其中有对有错,预测对的值占预测总值的比例
混淆矩阵计算:
类1:P1 = TP / (TP + FP)
类2:P2 = TN / (TN + FN)
类3:…
MPA:类别平均像素准确率
- 含义:分别计算每个类被正确分类像素数的比例,即:CPA,然后累加求平均
- 混淆矩阵计算:
- 每个类别像素准确率为:Pi(计算:对角线值 / 对应列的像素总数)
- MPA = sum(Pi) / 类别数
4 交并比 IOU
Intersection-Over-Union (IoU),也称为 Jaccard 指数,是语义分割中最常用的指标之一……这是有充分理由的。IoU 是一个非常简单的指标,非常有效。
定义:**IoU 是预测分割和标签之间的重叠区域除以预测分割和标签之间的联合区域(**两者的交集/两者的并集)如图所示。该指标的范围为 0–1 (0–100%),其中 0 表示没有重叠,1 表示完全重叠分割。
对于二元分类而言,其计算公式为:


还是上面那个3 * 3 的例子,我们来计算一下它的IoU

代码:
# IOU evaluation
def binary_iou(s, g):
assert (len(s.shape) len(g.shape))
# 两者相乘值为1的部分为交集
intersecion = np.multiply(s, g)
# 两者相加,值大于0的部分为交集
union = np.asarray(s + g > 0, np.float32)
iou = intersecion.sum() / (union.sum() + 1e-10)
return iou
g = np.array([1, 1, 1, 1, 1, 0, 0, 0, 0])
s = np.array([0, 1, 0, 1, 1, 0, 0, 0, 0])
iou = binary_iou(s, g)
print(iou)
如果理解了原理,代码依然很简单。
tips: 分母中加了一项1e-10, 是为了防止分母为0的情况出错。
IOU也有一些改进:如MIOU
MIoU:平均交并比
含义:模型对每一类预测的结果和真实值的交集与并集的比值,求和再平均的结果
混淆矩阵计算:
以求二分类的MIoU为例
MIoU = (IoU正例p + IoU反例n) / 2 = [ TP / (TP + FP + FN) + TN / (TN + FN + FP) ] / 2
5 骰子系数 Dice
定义: Dice系数定义为两倍的交集除以像素和,也叫F1 score。Dice 系数与 IoU 非常相似,它们是正相关的。这意味着如果一个人说模型 A 在分割图像方面比模型 B 更好,那么另一个人也会这么说。
与 IoU 一样,它们的范围都从 0 到 1,其中 1 表示预测和真实之间的最大相似度。
其公式为:

可以看到Dice系数对应于IoU,分子分母中的TP都取了两倍:
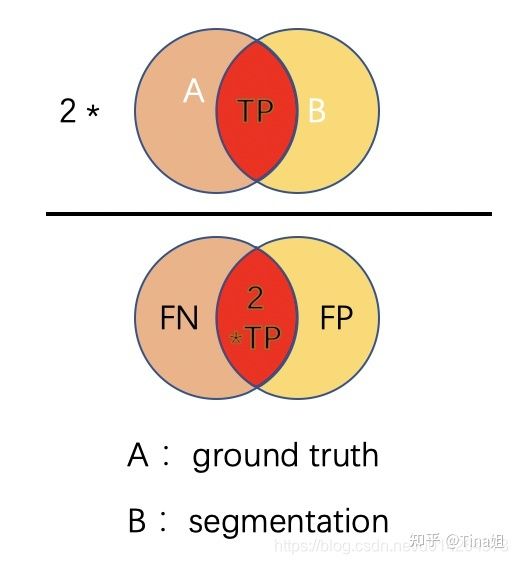
还是上面那个3 * 3 的例子,我们来计算一下它的Dice:

代码:
def binary_dice(s, g):
"""
calculate the Dice score of two N-d volumes.
s: the segmentation volume of numpy array
g: the ground truth volume of numpy array
"""
assert (len(s.shape) len(g.shape))
prod = np.multiply(s, g)
s0 = prod.sum()
dice = (2.0 * s0 + 1e-10) / (s.sum() + g.sum() + 1e-10)
return dice
g = np.array([1, 1, 1, 1, 1, 0, 0, 0, 0])
s = np.array([0, 1, 0, 1, 1, 0, 0, 0, 0])
dice = binary_dice(s, g)
print(dice)
6 敏感度Sensitivity
7 阳性预测值 PPV
8 表面距离计算
当我们评价图像分割的质量和模型表现时,经常会用到各类表面距离的计算。 比如
- Average surface distance 平均表面距离
- Hausdorff distance 豪斯多夫距离
- Surface overlap 表面重叠度
- Surface dice 表面dice值
- Volumetric dice 三维dice值
主要讲述豪斯多夫距离。
8.1 Hausdorff distance 豪斯多夫距离
将Hausdorff distance, HD 用于分割指标,主要是用来度量边界的分割准确度
Dice对mask的内部填充比较敏感,而hausdorff distance 对分割出的边界比较敏感。
Hausdorff_95就是是最后的值乘以95%,目的是为了消除离群值的一个非常小的子集的影响。
其计算公式为:


计算流程:
给定两个点集合A{ a0, a1, … }和B{ b0, b1, b2, …}
- 取A集合中的一点a0,计算a0到B集合中所有点的距离,保留最短的距离d0
- 遍历A集合中所有点,图中一共两点a0和a1,计算出d0和d1
- 比较所有的距离{ d0, d1 },选出最长的距离d1
- 这个最长的距离就是h,它是A→B的单向豪斯多夫距离,记为h( A, B)
- 对于A集合中任意一点a,我们可以确定,以点a为圆心,h为半径的圆内部必有B集合中的
- 交换A集合和B集合的角色,计算B→A的单向豪斯多夫距离h( B, A ),选出h( A, B )和h( B, A )中最长的距离,就是A,B集合的双向豪斯多夫距离

在实际计算中,我们并不是选取的不是最大距离,而是将距离从大到小排列后,取排名为95%的距离。这么做的目的是为了排除一些离群点所造成的不合理的距离,保持整体数值的稳定性。所以也叫HD95.
代码实现:
pip install -i https://pypi.tuna.tsinghua.edu.cn/simple numba
pip install hausdorff
numpy代码示例:
import numpy as np
from hausdorff import hausdorff_distance
# two random 2D arrays (second dimension must match)
np.random.seed(0)
X = np.random.random((1000,100))
Y = np.random.random((5000,100))
# Test computation of Hausdorff distance with different base distances
print("Hausdorff distance test: {0}".format( hausdorff_distance(X, Y, distance="manhattan") ))
print("Hausdorff distance test: {0}".format( hausdorff_distance(X, Y, distance="euclidean") ))
print("Hausdorff distance test: {0}".format( hausdorff_distance(X, Y, distance="chebyshev") ))
print("Hausdorff distance test: {0}".format( hausdorff_distance(X, Y, distance="cosine") ))
# For haversine, use 2D lat, lng coordinates
def rand_lat_lng(N):
lats = np.random.uniform(-90, 90, N)
lngs = np.random.uniform(-180, 180, N)
return np.stack([lats, lngs], axis=-1)
X = rand_lat_lng(100)
Y = rand_lat_lng(250)
print("Hausdorff haversine test: {0}".format( hausdorff_distance(X, Y, distance="haversine") ))
9 快速实现指标的工具和代码
医学图像处理的python库medpy:
http://loli.github.io/medpy/metric.html
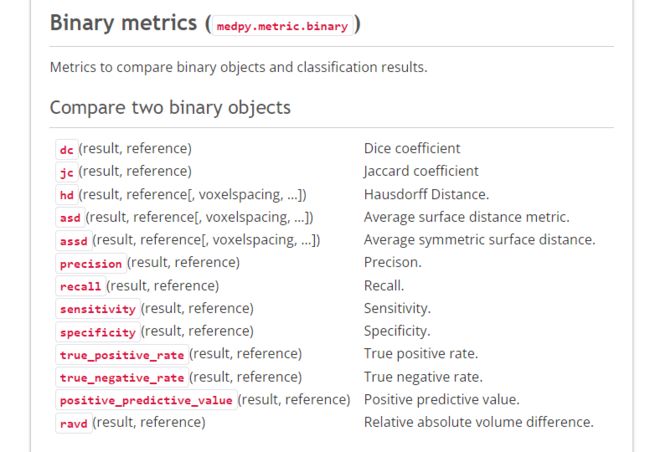
以上各个指标的pytorch代码都是参考medpy包中的代码,那我们如何快速实现这些指标呢?直接掉包。
from medpy import metric
def calculate_metric_percase(pred, gt):
dice = metric.binary.dc(pred, gt)
jc = metric.binary.jc(pred, gt)
hd = metric.binary.hd95(pred, gt)
asd = metric.binary.asd(pred, gt)
return dice, jc, hd, asd
参考:
【分割常用评价指标Dice、Hausdorff_95、IOU、PPV等(打马)】
https://zhuanlan.zhihu.com/p/117435908
【【理论+实践】史上最全-论文中常用的图像分割评价指标-附完整代码】
https://zhuanlan.zhihu.com/p/378796770
【特异度(specificity)与灵敏度(sensitivity)】
https://www.jianshu.com/p/7919ef304b19
【医学图像分割常用指标及代码(pytorch)】
https://blog.csdn.net/qq_36484003/article/details/114363112



