高速缓存Cache详解(西电考研向)
西电计组 考研笔记
内容较多 建议收藏
持续更新 欢迎关注
文章目录
- 高速缓存Cache详解
-
- 一.Cache概述及引入背景
- 二.地址映射与变换
-
- 1.全相联地址映射方式
- 2.直接地址映射方式
- 3.组相联地址映射方式(重要)
- 4.多路组相联
- 5.例题分析
- 三.Cache替换算法
- 四.Cache更新策略
- 五.Cache性能分析
-
- 1.Cache的性能度量
- 2.Cache的性能提升
- 3.例题分析
高速缓存Cache详解
一.Cache概述及引入背景
由于CPU的速度提升一直高于存储器的速度提升,与CPU速度相匹配的高速存储器价格昂贵,以至于产生的矛盾是:如果使用低价的慢速存储器作为主存,无法使CPU的速度发挥出来;而如果使用高价的高速存储器作为主存,价格又令人无法接受。高速缓存Cache的出现就是用来解决这样的矛盾的。
局部性原理:
高速缓冲存储器Cache的工作建立在程序与数据的局部性原理之上,即在一段较短的时间间隔内,程序集中在某一较小的主存地址空间上执行,同样对数据的访问也存在局部性现象。
Cache的概念:
基于程序及数据的局部性原理,在CPU和主存之间(尽量靠近CPU的地方)设置一种容量较小的高速存储器,将当前正在执行的程序和正在访问的数据放入其中。在程序运行时,不需要从慢速的主存中取指令和数据,而是直接访问这种高速小容量的存储器,从而可以提高CPU的程序执行速度,这种存储器就称为高速缓冲存储器,简称Cache。
- Cache一般是由SRAM实现的。(按地址访问)
- 地址映射表一般是由相联存储器实现的。(按内容/地址访问)
- Cache的管理工作大部分需要由硬件来实现
二.地址映射与变换
主存地址到Cache地址的地址映射:
在Cache工作过程中,需要将主存的信息拷贝到Cache中,这就需要建立主存地址与Cache地址之间的映射关系,并将该关系存入地址映射表中。
若检索到要读写的主存信息的地址在Cache地址映射表中,则称为”命中“;若不在地址映射表中,则称为”未命中“。
地址变换:
在程序执行时,如果命中,则CPU就可以从Cache中存取信息,此时需要将主存地址转换为Cache地址才能对Cache进行访问。将主存地址转换为Cache地址称为地址变换。
注意:
主存地址的划分(区号,块号,块内地址)是人为进行逻辑划分的,实际上并没有改变主存地址的原本形式,主存地址的划分仍然是由寻址空间决定的。
地址映射与地址变换有三种基本方式:
1.全相联地址映射方式
Cache与主存的分块
将Cache和主存分成若干容量相等的存储块。例如主存容量64MB,Cache容量32KB,以4KB大小分块。则Cache被分为8块,块号0~7,可用3位二进制编码表示。而主存被分为16K个块,块号0 ~16383,可用14位二进制编码表示。
全相联映射规则:
主存的任何一块可以装入(拷贝)到Cache中的任何一块。
Cache块号作为地址映射表的表项地址(即相联存储器的单元地址),然后在相联存储器的存储单元中记录装入的Cache的主存块的块号(即标记)。
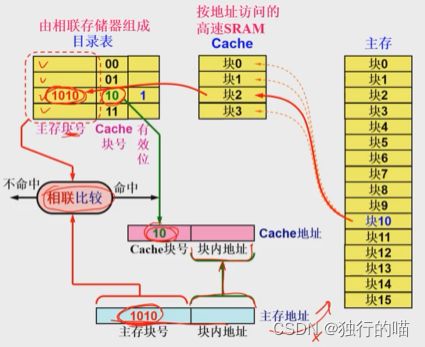
全相联映射方式工作过程:
假如CPU通过地址总线给出要访问的地址在主存的第10块,此时主存地址被加载到主存的同时也被加载到Cache的地址映射与变换模块上。在地址映射表中没有检索到主存第10块的内容(图中映射表中无内容,有效位全部置0),则表示未命中。此时需要通过访问主存并将主存第10块的存储内容装入Cache中的任意一块当中,假如此时装入Cache的第2块。
在将主存第10块装入Cache第2块的同时需要建立地址映射表中的内容:
- 将地址映射表中第2个表项(Cache块号为2)的有效位置1
- 将主存块号10即1010存入该表项
当下次再次访问主存第10块中的内容时,则会命中,然后废除对主存的访问,通过地址映射表得知主存块号对应的Cache块号后,直接访问Cache中的第2块来对内容进行存取。
全相联地址映射方式的优缺点
-
全相联地址映射方式的优点: 主存装入Cache灵活,可以装入任意一块。只有当Cache全部装满后才需要替换。
-
全相联地址映射方式的缺点: 全相联映射的代价最高,要求相联存储器容量最大,需要检索相联存储器的所有单元才可能获得Cache的块号,地址变换机构最复杂。
2.直接地址映射方式
主存的分区
直接地址映射方式下,逻辑上对主存进行分区。每一个区的大小即是Cache的容量大小。举例:假设Cache的容量为32KB,主存的大小为64MB,则每一个分区的大小应与Cache的大小一致,为32KB,可将主存分为 64 M / 32 K = 2 K 64M/32K=2K 64M/32K=2K个区,区号从0到2047.然后Cache和主存的每个区再以4KB分块。
直接映射规则:
主存各区中块号相同的存储块只能装入Cache中相同块号的存储块中
例如所有区中的0号块只能装入Cache中的0号块中,主存中的1号块只能装入Cache中的1号块中,以此类推。这种映射方式使主存块号与Cache块号保持一致。
直接映射地址变换
主存地址在逻辑上被分为:区号,区内块号,块内地址 三个部分
以上述举例为背景,即:
- 将主存分为了2K个区,
- 每个区的分为8个块,
- 每个块大小位4KB
当CPU给出访问的主存地址为:28B57A4H时,对该地址的逻辑划分如下:
| 区号(11位) | 区内块号(3位) | 块内地址(12位) |
|---|---|---|
| 10100010110 | 101 | 011110100100 |
对上述划分情况做简要分析:
- 分区个数为2K,故区号需要11位二进制数表示,所以高11位为区号
- 每个区内分为8块,故块号需要3位二进制数表示,所以接下来3位为块号
- 每个块的大小为4KB,内存以字节编址,一个存储单元的大小为1B,所以一个块内有4K个存储单元,对4K个存储单元进行编址需要12位二进制数表示,所以低12位为块内地址。
直接映射方式工作过程
CPU通过地址总线给出的主存地址首先被同时传送到主存和Cache地址变换与映射模块上,然后通过地址映射与变换:只需将主存块号作为地址映射表的地址去检索该单元存放的是否是本块主存地址的区号,即只需要检测地址映射表中的一个存储单元即可。(映射)若命中,则由主存地址直接获得Cache地址。(变换)
如果主存地址在Cache中命中,则废除对主存的访问,直接从Cache中相应的块里存取要访问的内容。
如果主存地址在Cache中未命中,则需要继续对主存内容进行访问,并将主存中访问的块装入Cache对应的块中。

直接地址映射方式的优点
直接映射方式下地址变换简单,并且对地址映射表的检索速度快,只需检索一个表项即可。地址映射表可由静态存储器构成,硬件实现简单。
直接地址映射方式的缺点
直接地址映射方式的缺点是效率低,当Cahce某一块正在使用而主存中其他区的同一块号的块又需要装入时,只能将正在使用的Cache块进行替换,即便Cache中其他块目前都是空闲的状态。
如果出现主存中不同区的相同块号的块被频繁交替访问时,就会出现这些块被频繁装入和替换的情况,将大大影响Cache的命中率,因此直接地址映射适合于大容量Cache(块号多的Cache)
3.组相联地址映射方式(重要)
全相联地址映射和直接地址映射方式各有优缺点,组相联地址映射方式就是将两者的优点结合而尽可能缩小两者的缺点。
组划分与块划分
组相联地址映射的存储结构是将Cache先分组,组内再分块。
而主存结构是先以Cache容量分区,区内按Cache的方法分组,组内再分块。
组相联地址映射规则
组相联地址映射规则为:主存与Cache间的地址映射是组间直接映射而组内全相联映射,也就是说主存某组内的块只能装入Cache的同号组中,但可以装入Cache同号组中的任意一块内。 相联映射表中需要记录主存区号和组内块号。
组相联地址映射方式将相联比较的范围缩小到某一范围内,在提供一定灵活度的同时有效缩小了相联存储器的规模。
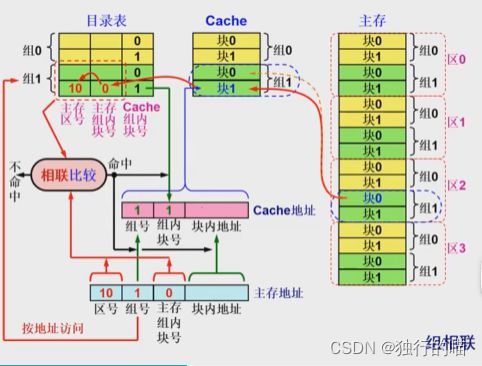
组相联地址映射工作过程
组相联地址映射的工作过程与上面两种的不同之处在于:
地址映射有所区别:组相联的地址映射过程比全相联地址映射简单,但是比直接地址映射复杂。由于组相联地址映射下,主存中某一个组内的块只能存储于Cache对应的同号组内,所以在检索地址映射表时,我们只需要检测地址映射表中对应组号范围内的表项即可。 以下图为例,假如我们需要访问的是主存中:第2区中第1组的第0块,那么我们只需要将检索范围缩小到目录表的后两行,即目录表中第1组的存储范围内。然后对该范围内中每一个表项中的区号和组内块号进行并行比较,假如有区号和组内块号同时和主存地址相同的某一行,则说明Cache命中。
此时的地址变换则同样比较简单,假如命中,则将该表项中对应的Cache组内块号取出,我们就知道了主存块在Cache中对应的块号,再与组号和块内地址加以拼接就得到了Cache内的地址。
假如未命中,就需要将正在访问的主存块的内容尝试存入Cache,同样需要检索地址映射表来查看是否产生块冲突,检索时依然只需要在同组号的范围内检索目录表,检索范围较小。如果同组内有空闲块则可以将主存块存入该Cache空闲块中。发生冲突的概率相比于直接地址映射大大减小。
组相联映射的优缺点
优点:
- 块冲突概率比较低
- 块的利用率大幅提高
- 块的失效率明显降低
缺点:
- 实现难度和造价比直接映射高
4.多路组相联
多路划分及与组相联的联系
- n路组相联的组内分块规则为:n路组相联即每组n块。
- Cache按照组的数量分路,主存按照组的数量分区:例如,如果Cache共4组,则Cache每4块为1路,即每一路中都有各组的一块存在;主存每4块为一个区,
- 主存某一区的块只能装入每一路路内块号等于该区内块号的那一块。所以Cache的路内块号,主存的区内块号,都可以理解为组号。
- 主存地址划分中的索引(index)字段,其含义是主存的区内块号,或Cache路内块号,也即组号。
- 在进行主存-Cache地址映射时,如果要把主存第3区的第2块(即第2组)装入Cache,可以装入Cache第2组的任何一块(第2组由所有路的第2块构成),即组间直接映射,组内全相联映射,符合组相联地址映射的一般规则。
主存地址划分:
| 标记(区号) | 索引(组号) | 块内地址 |
|---|
多路组相联的主存地址划分有别于之前的组相联地址划分:
- 在多路组相联中,主存先分区,区内直接分块
- 其中,分区的多少与组数量有关,每个区内包含的块数等于组数
- 地址划分中的标记等同于主存区号,索引等同于组号或区内块号
- 新的地址划分中主存区内块号的概念等同于组号
- 组数的划分又与路数有关,n路组相联即每组n块,假如Cache共m块,则每路有m/n块,即共分为m/n组。(路内块号等同于组号)
2路组相联CPU访问过程
以2路组相联为例,CPU读主存数据时命中Cache,只需以下三步,即可从Cache中得到所需要的数据:
- (1)根据主存地址中的索引字段(即组号,主存区内块号,路内块号),按地址访问,读取地址映射表上,下两路的第2行;同时,根据主存地址的索引,块内地址字段按地址访问,读取Cache上,下两路第2块内部地址为24的字节数据。
- (2)地址映射表上,下两路第2行的内同被读出,分别作为两个数字比较器的输入(有效位和标记字段分别连接数字比较器的G,B两个输入端),数字比较器A输入段的数据由主存地址的标记(Tag)字段,即主存区内块号提供;同时Cache上,下两路第2块内部地址为24字节数据被读出,作为2选1选择器的左右两路输入。
- (3)经过比较,Cache第1路的第2块不是主存第3区第2块的内容,第1路数字比较器的输出为假;Cache第2路的第2块是主存第3区第2块的内容,第2路数字比较器输出为真。两个数字比较器的输出信号控制2选1控制选择器,使左侧的输入(即Cache第2路第2块内部地址为23的字节数据)到达输出,送至CPU。
5.例题分析
例题2:(2018)(本题为新书改版前的真题,部分知识点存在一定冲突)
某计算机系统主存总容量为4GB,按字节编址。为提升主存速度,创建Cache系统,其采用8路组相联映射,且容量为256KB,分为8组。
(1)设主存地址结构为:主存区号+组号+块号+块内地址,则主存和Cache地址各字段位数为多少?每次进行MM->Cache地址变换时,需要参与相联比较的位数是多少?
分析:
- 主存按照Cache大小分区:4GB/256KB= 2 14 2^{14} 214区,则主存区号14位
- Cache分为8组,组号3位
- 由于是8路组相联,所以每组分为8块;组内块号0~7为3位
- 相联比较时,需要比较主存区号与块号,即14+3=17位
故主存的地址各字段为:
- 主存区号14位;组号3位;组内块号3位;块内地址12位
Cache的地址各字段为:
- 组号3位;组内块号3位;块内地址12位
需要相联比较的位数为:17位
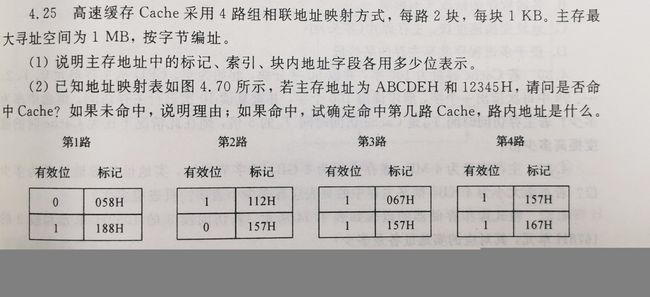
(2)若MM-Cache地址变换表中有效内容如下表,当CPU访问主存的地址分别为01234567H和FEDCBA98H时,问是否命中Cache?若命中,给出相应的Cache地址。
| 地址 | 主存区号 | 组内块号 | 有效位 |
|---|---|---|---|
| 000000 | 0009H | 000B | 1 |
| 001011 | 3FD7H | 010B | 1 |
| 001110 | 2440H | 101B | 1 |
| 011001 | 3FD7H | 011B | 1 |
| 011110 | 076EH | 111B | 1 |
| 110000 | 0048H | 100B | 1 |
| 110100 | 0009H | 000B | 1 |
| 111111 | 0048H | 100B | 1 |
分析:
将主存地址01234567H展开成2进制,按照主存地址结构分析得:
- 01234567H=0000 0001 0010 0011 0100 0101 0110 0111B
- 块内地址: 0101 0110 0111B
- 组内块号:100B
- 组号:110B
- 区号:0000 0001 0010 00B=0048H
将主存地址FEDCBA98H展开成2进制,按照主存地址结构分析得:
- FEDCBA98H=1111 1110 1101 1100 1011 1010 1001 1000B
- 组内地址:1010 1001 1000B
- 组内块号:011B
- 组号:001B
- 区号:1111 1110 1101 11B=3FB7H
分析表格:
- 表格左侧的地址为Cache的地址,前3位为Cache组号,后3位为组内块号
- 由于采用组相联映射,所以Cache的组号应和主存地址的组号直接映射;而组内块号采用全相联映射
- 由于01234567H的组号为110,所以定位到地址映射表组号为110的行,通过比较区号和组内块号得出01234567H地址命中Cache
故01234567HCache地址的组号和组内块号为:110000;与主存块内地址一起构成Cache地址:110000 0101 0110 0111B
同理分析表格发现FEDBCA98H未命中
(3)若将Cache改为2级结构,其性能参数如下:
| 级 | 局部命中率 | 缺失惩罚 |
|---|---|---|
| L1 | 0.95 | 5ns |
| L2 | 0.8 | 20ns |
解析:
Cache-主存系统的平均访问时间为:
解法1: 1 + ( 1 − 0.95 ) × 5 + ( 1 − 0.95 ) × ( 1 − 0.8 ) × 20 = 1.45 n s 1+(1-0.95)\times5+(1-0.95)\times(1-0.8)\times20=1.45ns 1+(1−0.95)×5+(1−0.95)×(1−0.8)×20=1.45ns
解法2: 0.95 + 0.05 × ( 0.8 × ( 5 + 1 ) + 0.2 × ( 5 + 1 + 20 ) ) = 1.45 n s 0.95+0.05\times(0.8\times(5+1)+0.2\times(5+1+20))=1.45ns 0.95+0.05×(0.8×(5+1)+0.2×(5+1+20))=1.45ns
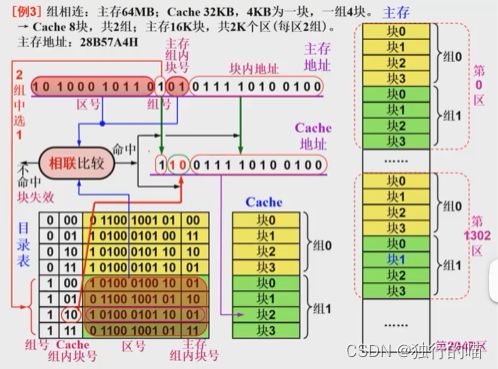
例题3
(1)解析:
- 采用4路组相联即每组4块,每路两块即共2组(路内块号等同于组号),Cache共8块
- 主存按照组数分区:主存区数= 1 M B / ( 2 × 1 K B ) = 2 9 区 1MB/(2\times1KB)=2^9区 1MB/(2×1KB)=29区,标记即区号,共9位
- 索引等同于组号,共分2组,索引共1位
- 块大小为1KB,按字节编址,共1K个单元,块内地址共10位
(2)解析:
-
主存地址ABCDEH展为2进制数:1010 1011 1(标记)1(索引)00 1101 1110(块内地址)
-
标记(区号):157H
-
索引(组号):1
-
由图中地址映射表可知,ABCDEH命中,即第3路Cache
-
路内地址为:索引+块内地址=1 00 1101 1110
-
主存地址12345H展为2进制数:0001 0010 0(标记)0(索引)11 0100 0101(块内地址)
-
标记(区号)024H
-
索引(组号)0
-
由图中地址映射表可知,12345H未命中
三.Cache替换算法
1.随机替换算法(RAND)
该算法是用随机函数发生器产生需要替换的Cache块号,将其替换。这种方法没有考虑信息的历史及使用情况,可能会降低命中率,但实现简单,并且当Cache容量很大时,RAND算法的实际表现不错。
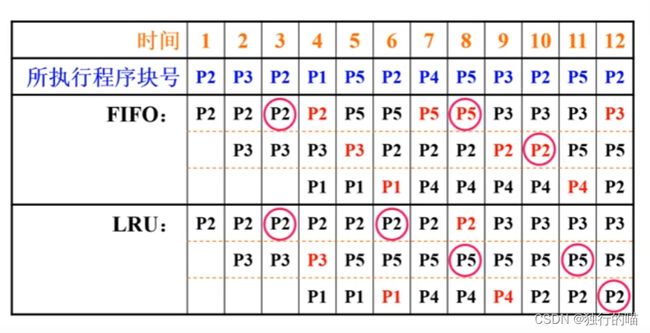
2.先进先出算法(FIFO)
该算法是将最先装入Cache的那个主存块替换出去。这种方法只考虑了信息的历史情况而没有考虑其使用情况,也许最先装入的那一块正在频繁使用。
3.最不经常使用算法(LFU)
该算法是将一段时间内被访问次数最少的Cache块替换出去。对每个Cache块设置一个计数器,且开始时置0,Cache块每被访问一次,其计数器就加1.当需要替换时,便将计数值最小的块替换出去,同时所有计数器清0.这种方法将计数周期限定在两次替换时间间隔内,不能完全反映近期的访问情况。
4.最久未用算法(LRU)
该算法是将近期最少使用的Cache块替换出去。这种算法需要对每个Cache块设置一个计数器,某块每命中一次,就将其计数器清0而其他块的计数器加1,记录Cache中个块的使用情况。当需要替换时,便将其中计数值最大的块替换出去。该算法利用了局部性原理。
5.最优替换算法(OPT)
根据执行一遍后的信息,根据Cache块的使用情况得知替换的最优策略来进行替换。
这种方法无法实现,只能作为衡量其他算法优劣的标准
四.Cache更新策略
1.写回法
写回法是当CPU写Cache命中时,只将数据写入Cache而不利己写入主存。只有当由CPU改写过的Cache块被替换出去时该块才写回到主存中。
如果CPU写Cache未命中,则先将相应主存块调入Cache中,再在Cache中进行写入操作。对主存的修改仍在该块被替换出去时进行。
写回法的实现需要对Cache的每一块增设1位修改标志,以便在该块被替换时决定其丢弃还是写回主存。写回法的速度较快,但是可能会引发主存与Cache内容不一致的问题。
2.写直达法(RAND)
写直达法也称作全写法,是当CPU写Cache命中时,在将数据写入Cache的同时也写入主存,从而较好地保证了主存与Cache内容的一致性。
当CPU写Cache未命中时,就直接对主存进行写入修改,而后可以将修改过的主存块调入或不调入Cache。
写直达法不需要增设修改标志,速度较慢但是可以保证主存和Cache内容一致。
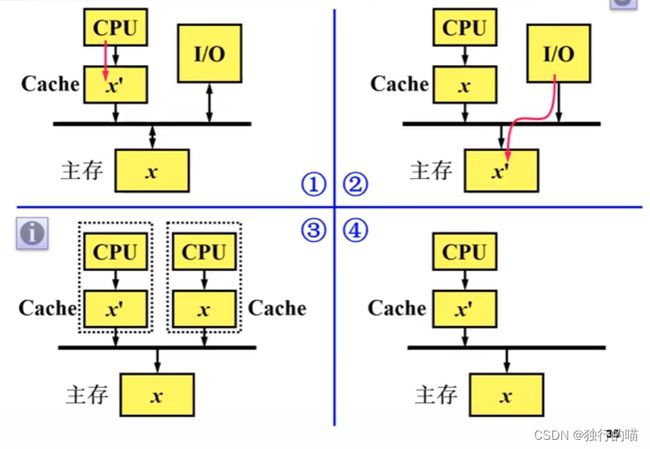
下图是几中不同的计算机结构中,写Cache时Cache与主存内容一致性的问题的情况:
五.Cache性能分析
1.Cache的性能度量
1).命中率
命中率h的定义为: h = N c N × 100 % h=\frac{N_c}{N}\times100\% h=NNc×100%
- 其中Nc为命中Cache的次数,N为访问Cache-主存系统的总次数
2).平均访问时间
Cache的访问时间为 T c T_c Tc,主存的访问时间为 T M T_M TM,Cache命中率为h
则两层结构的Cache-主存系统的平均访问时间T可表示为:
T = h × T c + ( 1 − h ) × ( T c + T M ) = T c + ( 1 − h ) × T M T=h\times{T_c}+(1-h)\times(T_c+T_M)=T_c+(1-h)\times{T_M} T=h×Tc+(1−h)×(Tc+TM)=Tc+(1−h)×TM
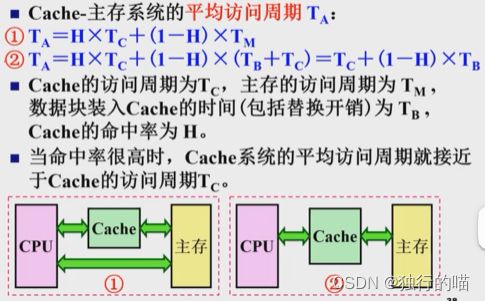
注意区别:主存-Cache系统的平均访问时间与Cache系统的平均访问时间
- 主存-Cache系统的平均访问时间是指访问一个在主存-Cache系统中的数据块所需的平均时间,即该数据块有可能未命中Cache但它一定保底存在于主存之中。
- Cache系统的平均访问时间是指访问一个存在于Cache系统中的数据块所需的平均访问时间,即该数据块一定存在于Cache中,但不确定存在于哪一级Cache之中。
3).加速比
Cache-主存系统的加速比Sp定义为:
S p = T M T = T M T c + ( 1 − h ) T M = 1 1 − h + 1 r S_p=\frac{T_M}{T}=\frac{T_M}{T_c+(1-h)T_M}=\frac{1}{1-h+\frac{1}{r}} Sp=TTM=Tc+(1−h)TMTM=1−h+r11
- 其中r=TM/Tc为从主存到Cache速度提升的倍数。
- 加速比Sp的极限值为r=TM/Tc
2.Cache的性能提升
1)多级Cache
以两级Cache为例,将L1Cache(更靠近CPU)做得容量比较小,但速度很高,与CPU相匹配;将L2Cache做得容量比较大,但速度介于L1Cache和主存之间。当L1Cache未命中时,则到L2Cache中去搜索,由于L2Cache容量大,命中率会很高。
两 级 C a c h e 的 总 缺 失 率 = L 1 缺 失 率 × L 2 缺 失 率 两级Cache的总缺失率=L1缺失率\times L2缺失率 两级Cache的总缺失率=L1缺失率×L2缺失率

2)降低Cache的缺失率
- 合理设计Cache块尺寸
- 合理增加Cache容量
- 合理设置相联度
- 硬件预取
- 编译优化
3)减少Cache开销
3.例题分析
例题1:

程序代码分析: 该程序段的功能是,在int整型数组a中,从下标0到999,这1000个数组单元中,每次取一个数,并给该数值+32后再写回数组单元中。这样对每一个数组单元都要进行一次读和一次写操作,也就说每一次循环需要两次访问主存的操作。每次访问访问主存前都会尝试访问Cache。
考虑Cache的分块情况: Cache一个块的大小为16B,而一个数组单元int变量的大小为4B,所以一个Cache块中可以装4个数组单元。
考虑Cache的地址映射放式: 题中Cache采用直接地址映射的方式,直接地址映射在重复来回访问主存不同区的同号块时可能频繁产生块冲突,但是在该程序的逻辑下,每一个块都只可能被装入一次访问完成后就不再会对该块重复访问了,即对数据的访问是连续顺序执行的。所以该题目的解答不需要额外考虑直接地址映射产生的冲突情况。
现在考虑程序执行过程中Cache的命中与装入情况:
第一次循环执行时,由于Cache是空的状态,所以必然未命中,此时将正在访问的块装入Cache中,也就是4个连续数组单元a[0],a[1],a[2],a[3]的内容。之后对数组单元a[0]的写入操作将会命中,然后对a[1],a[2],a[3]的读写访问操作都会命中,在对这一个块内单元的操作中,一共进行了8次内存访问,4次读访问,4次写访问,其中只第一次对a[0]的读访问未命中,即缺失。所以8次访问中,缺失率为1/8。之后的情形与上面类似,当对a[4]进行读访问未命中时,又会继续装入包含后面4个单元的主存块,之后的7次访问都将命中,以此类推,所以总的缺失率仍然为1/8。