GAMES101作业2

作业内容

在屏幕上画出一个实心三角形，
换言之，栅格化一个三角形。上一次作业中，在视口变化之后，我们调用了函数
rasterize_wireframe(const Triangle& t)。但这一次，你需要自己填写并调用
函数 rasterize_triangle(const Triangle& t)。
该函数的内部工作流程如下：

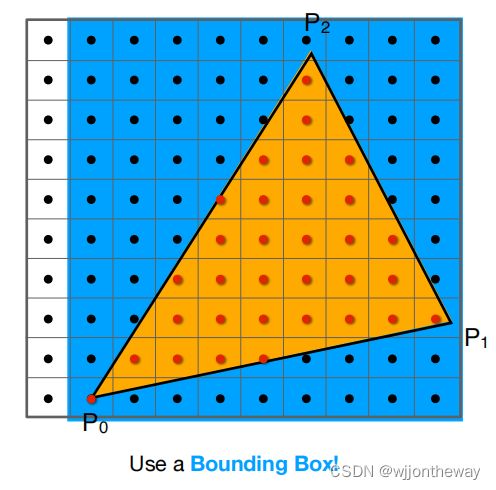
1. 创建三角形的 2 维 bounding box。
2. 遍历此 bounding box 内的所有像素（使用其整数索引）。然后，使用像素中
   心的屏幕空间坐标来检查中心点是否在三角形内。
3. 如果在内部，则将其位置处的插值深度值 (interpolated depth value) 与深度
   缓冲区 (depth buffer) 中的相应值进行比较。
4. 如果当前点更靠近相机，请设置像素颜色并更新深度缓冲区 (depth buffer)。

Step 1. 创建三角形的2维bounding box

GAMES101_Lecture_05.pdf 43页

• Checking All Pixels on the Screen?
  
  已知三角形的三个顶点，如何得出蓝色矩形的width 和 height。 或者说左下角点和右上角的坐标

假设三角形的三个顶点经过t.toVector4( )输出的坐标如下：

===== P0 ======
108.579
350
-0.714285
1
===== p1 ======
350
108.579
-0.714285
1 
===== p2 ======
591.421
350
-0.714285
1

那么bounding box 左下角和右上角的坐标为

B_1_x = min(P0_x, P1_x, P2_x)
B_1_y = min(P0_y, P1_y, P2_y)

B_2_x = max(P0_x, P1_x, P2_x)
B_2_y = max(P0_y, P1_y, P2_y)

bounding_box_width = B_2_x - B_1_x;
bounding_box_height = B_2_y - B_1_y;

    unsigned int bBox_leftbottom_x;
    unsigned int bBox_leftbottom_y;
    unsigned int bBox_topright_x;
    unsigned int bBox_topright_y;
    unsigned int width, height;

    bBox_leftbottom_x = floor(MIN(MIN(v[0].x(), v[1].x()), v[2].x())); //向下取整
    bBox_leftbottom_y = floor(MIN(MIN(v[0].y(), v[1].y()), v[2].y()));
    bBox_topright_x   = ceil(MAX(MAX(v[0].x(), v[1].x()), v[2].x()));  //向上取整
    bBox_topright_y   = ceil(MAX(MAX(v[0].y(), v[1].y()), v[2].y()));
    std::cout << "bBox :leftbottom:(" << bBox_leftbottom_x <<
              ","<<bBox_leftbottom_y <<") "<<
              "topright:("<<bBox_topright_x <<
              ","<< bBox_topright_y <<")" << std::endl;
    width = bBox_topright_x - bBox_leftbottom_x;
    height = bBox_topright_y - bBox_topright_y;

x: 108.579 y: 350 z: -0.714285
x: 350 y: 108.579 z: -0.714285
x: 591.421 y: 350 z: -0.714285
bBox :leftbottom:(108,108) topright:(592,350)
bBox_width:484
bBox_height:242

Step 2. 判断bBox中的像素中心点是否在三角形内

遍历此 bounding box 内的所有像素（使用其整数索引）。然后，使用像素中心的屏幕空间坐标来检查中心点是否在三角形内。

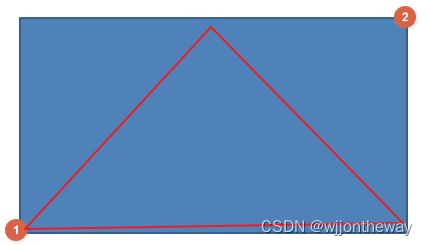
在Lecture 2中，判断一个点是否在三角形内，可以通过某个顶点到该点的向量与边的叉乘是否都满足z坐标的一致性，比如上图中判断(按逆时针方向)

• $P_0{P}_1$ x $P_0{P}_Q$
• $P_1{P}_2$ x $P_1{P}_Q$
• $P_2{P}_0$ x $P_2{P}_Q$

借助Egien提供的向量叉乘的接口

v1_tmp = vector_3f_p0p1.cross(vector_3f_p0pq);
v2_tmp = vector_3f_p1p2.cross(vector_3f_p1pq);
v3_tmp = vector_3f_p2p1.cross(vector_3f_p2pq);

static bool insideTriangle(int x, int y, const Vector3f* _v)
{   
    // TODO : Implement this function to check if the point (x, y) is inside the triangle represented by _v[0], _v[1], _v[2]

    Vector3f q = Vector3f(x, y, 1.0);                    // Homogeneous
    Vector3f p0_pq = q - _v[0];
    Vector3f p1_pq = q - _v[1];
    Vector3f p2_pq = q - _v[2];

    Vector3f v1_tmp = (_v[1] - _v[0]).cross(p0_pq);       //p0_p1 x p0_pq
    Vector3f v2_tmp = (_v[2] - _v[1]).cross(p1_pq);       //p1_p2 x p1_pq
    Vector3f v3_tmp = (_v[0] - _v[2]).cross(p2_pq);       //p2_p0 x p2_pq

    if ((v1_tmp.z() > 0 && v2_tmp.z() > 0 && v3_tmp.z() > 0) ||
        (v1_tmp.z() < 0 && v2_tmp.z() < 0 && v3_tmp.z() < 0) ||
        (v1_tmp.z() < 1e-6 && v2_tmp.z() < 1e-6 && v3_tmp.z() < 1e-6))
    {
        return true;
    }
    else
    {
        return false;
    }
}   

Step 3. 比较插值深度和Depth Buffer

3. 如果在内部，则将其位置处的插值深度值 (interpolated depth value) 与深度
   缓冲区 (depth buffer) 中的相应值进行比较。
4. 如果当前点更靠近相机，请设置像素颜色并更新深度缓冲区 (depth buffer)。

注意，需要将工程的属性修改成兼容C++17, 否则下面语句报错

auto [alpha, beta, gamma] = computeBarycentric2D(x, y, t.v); 

for (int x = (int)bBox_leftbottom_x; x <= bBox_topright_x; x++)
{
    for (int y = (int)bBox_leftbottom_y; y <= bBox_topright_y; y++)
    {
        if (insideTriangle(x, y, t.v))
        {
            // If so, use the following code to get the interpolated z value.
            auto [alpha, beta, gamma] = computeBarycentric2D(x, y, t.v);
            float w_reciprocal = 1.0 / (alpha / v[0].w() + beta / v[1].w() + gamma / v[2].w());
            float z_interpolated = alpha * v[0].z() / v[0].w() + beta * v[1].z() / v[1].w() + gamma * v[2].z() / v[2].w();
            z_interpolated *= w_reciprocal;

            // compare the interpolated depth value with depth buffer value
            if (depth_buf[get_index(x, y)] > z_interpolated)
            {
                depth_buf[get_index(x, y)] = z_interpolated;
                // TODO : set the current pixel (use the set_pixel function) to the color of the triangle (use getColor function) if it should be painted.
                set_pixel(Vector3f(x, y, z_interpolated), t.getColor());
            }
        }
    }
}

MSAA

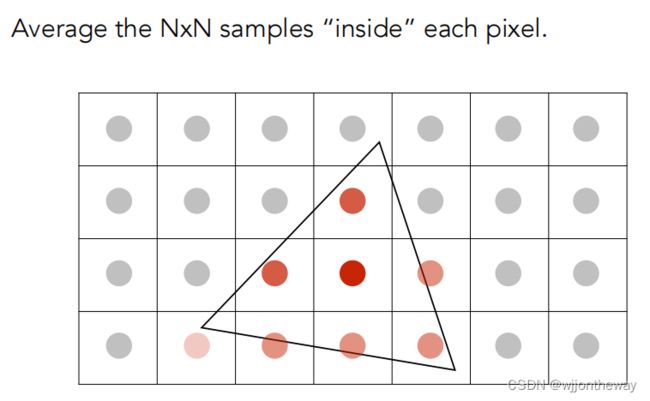
用 super-sampling 处理 Anti-aliasing : 你可能会注意到，当我们放大图像时，图像边缘会有锯齿感。我们可以用 super-sampling来解决这个问题，即对每个像素进行 2 * 2 采样，并比较前后的结果 (这里并不需要考虑像素与像素间的样本复用)。需要注意的点有，对于像素内的每一个样本都需要维护它自己的深度值，即每一个像素都需要维护一个 samplelist。最后，如果你实现正确的话，你得到的三角形不应该有不正常的黑边

for (int x = (int)bBox_leftbottom_x; x <= bBox_topright_x; x++)
 {
     for (int y = (int)bBox_leftbottom_y; y <= bBox_topright_y; y++)
     {
         float depth_tmp = 0.0;      // max value for float in system 
         int count = 0;
         Vector2f sample_point[4] = { Vector2f(0.25, 0.25),Vector2f(0.75, 0.25), Vector2f(0.75,0.75), Vector2f(0.75, 0.25) };
         for (int i=0; i<4; i++)
         {
             if (insideTriangle(x+ sample_point[i].x(), y+sample_point[i].y(), t.v))
             {
                 // If so, use the following code to get the interpolated z value.
                 auto [alpha, beta, gamma] = computeBarycentric2D(x, y, t.v);
                 float w_reciprocal = 1.0 / (alpha / v[0].w() + beta / v[1].w() + gamma / v[2].w());
                 float z_interpolated = alpha * v[0].z() / v[0].w() + beta * v[1].z() / v[1].w() + gamma * v[2].z() / v[2].w();
                 z_interpolated *= w_reciprocal;
                 depth_tmp += z_interpolated;
                 count +=1;
             }
         }
         float depth_average = depth_tmp / 4;
         if (count>0&&depth_buf[get_index(x,y)]> depth_average)
         {
             depth_buf[get_index(x, y)] = depth_average;

             set_pixel(Vector3f(x, y, depth_average), t.getColor() * count / 4.0 + frame_buf[get_index(x, y)] * (4 - count) / 4.0);
         }
         
     }
 }