Leetcode刷题4
⼆叉树、BFS、堆、Top K、⼆叉搜索树、模拟、图算法
一、二叉树
二叉树的前序中序后序
二叉树节点定义
为了方便演示,我们先定义一个二叉树节点类。
class TreeNode:
def __init__(self, val=0, left=None, right=None):
self.val = val
self.left = left
self.right = right前序遍历
前序遍历的顺序是先访问根节点,再遍历左子树,最后遍历右子树。可以用递归实现前序遍历,也可以用栈来实现。
递归
def preorderTraversal(root: TreeNode) -> List[int]:
res = []
def dfs(node):
if not node:
return
res.append(node.val)
# 先左后右
dfs(node.left)
dfs(node.right)
dfs(root)
return res栈
def preorderTraversal(root: TreeNode) -> List[int]:
if not root:
return []
res = []
stack = [root]
while stack:
node = stack.pop()
res.append(node.val)
if node.right:
stack.append(node.right)
if node.left:
stack.append(node.left)
return res
中序遍历
中序遍历的顺序是先遍历左子树,再访问根节点,最后遍历右子树。同样可以用递归或者栈来实现。
递归
def inorderTraversal(root: TreeNode) -> List[int]:
res = []
def dfs(node):
if not node:
return
# 先左 再访问 最后右
dfs(node.left)
res.append(node.val)
dfs(node.right)
dfs(root)
return res
栈
def inorderTraversal(root: TreeNode) -> List[int]:
if not root:
return []
res = []
stack = []
while stack or root:
while root:
stack.append(root)
root = root.left
node = stack.pop()
res.append(node.val)
root = node.right
return res
后序遍历
后序遍历的顺序是先遍历左子树,再遍历右子树,最后访问根节点。同样可以用递归或者栈来实现。
递归
def postorderTraversal(root: TreeNode) -> List[int]:
res = []
def dfs(node):
if not node:
return
dfs(node.left)
dfs(node.right)
res.append(node.val)
dfs(root)
return res
栈
def postorderTraversal(root: TreeNode) -> List[int]:
if not root:
return []
res = []
stack = [root]
while stack:
node = stack.pop()
res.append(node.val)
if node.left:
stack.append(node.left)
if node.right:
stack.append(node.right)
return res[::-1]
需要注意的是,栈实现后序遍历的时候,先遍历右子树再遍历左子树,然后将结果反转即可。
异型遍历
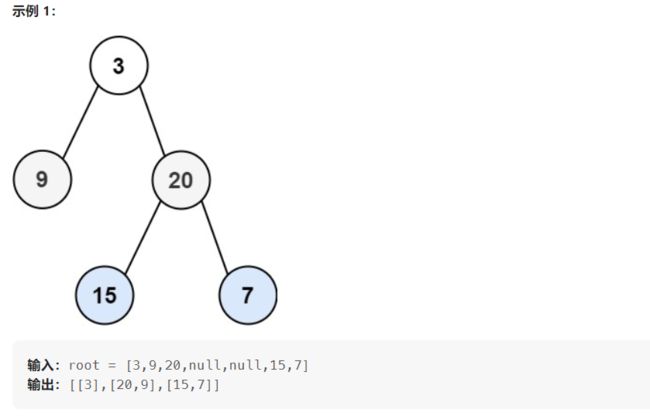
102. 二叉树的层序遍历
给你二叉树的根节点 root ,返回其节点值的 层序遍历 。 (即逐层地,从左到右访问所有节点)。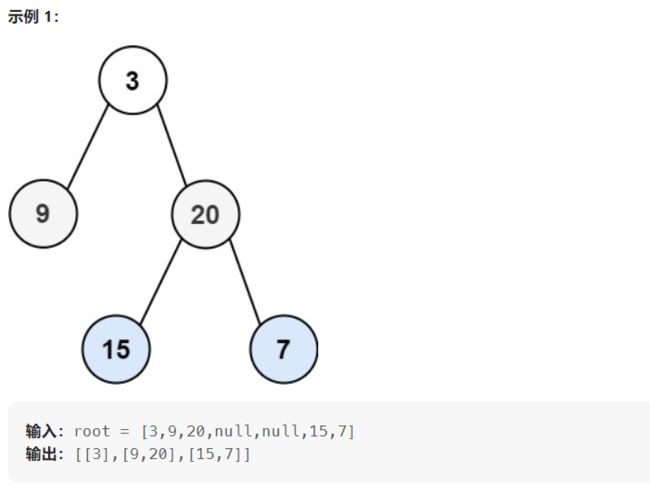
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def levelOrder(self, root: Optional[TreeNode]) -> List[List[int]]:
if root is None:
return []
ans = []
cur = [root]
while cur:
vals = []
nxt = []
for node in cur:
vals.append(node.val)
if node.left: nxt.append(node.left)
if node.right: nxt.append(node.right)
cur = nxt
ans.append(vals)
return ans优化,使用队列,保证当前cur中只保存待取的节点,那么每次访问完后就剔除队列即可。左出右进(先进先出)
class Solution:
def levelOrder(self, root: Optional[TreeNode]) -> List[List[int]]:
if root is None:
return []
ans = []
q = deque([root])
while q:
vals = []
for _ in range(len(q)):
node = q.popleft()
vals.append(node.val)
if node.left: q.append(node.left)
if node.right: q.append(node.right)
ans.append(vals)
return ans先保存根节点,然后先提取根节点的值,然后只要左右不为空就加到nxt中,待cur中的节点访问完毕后,把新的nxt赋值给cur,继续循环。
103. 二叉树的锯齿形层序遍历
给你二叉树的根节点 root ,返回其节点值的 锯齿形层序遍历 。(即先从左往右,再从右往左进行下一层遍历,以此类推,层与层之间交替进行)。
class Solution:
def zigzagLevelOrder(self, root: Optional[TreeNode]) -> List[List[int]]:
if root is None:
return []
ans = []
cur = [root]
even = False
while cur:
nxt = []
vals = []
for node in cur:
vals.append(node.val)
if node.left: nxt.append(node.left)
if node.right: nxt.append(node.right)
cur = nxt
# 奇数层不变,偶数层翻转
ans.append(vals[::-1] if even else vals)
even = not even
return ans105. 从前序与中序遍历序列构造二叉树
给定两个整数数组 preorder 和 inorder ,其中 preorder 是二叉树的先序遍历, inorder 是同一棵树的中序遍历,请构造二叉树并返回其根节点。
class Solution:
def buildTree(self, preorder: List[int], inorder: List[int]) -> TreeNode:
if not preorder or not inorder: # 递归终止条件
return
root = TreeNode(preorder[0]) # 先序为“根左右”,所以根据preorder可以确定root
idx = inorder.index(preorder[0]) # 中序为“左根右”,根据root可以划分出左右子树
# 下面递归对root的左右子树求解即可
root.left = self.buildTree(preorder[1:1 + idx], inorder[:idx])
root.right = self.buildTree(preorder[1 + idx:], inorder[idx + 1:])
return root114.二叉树展开为链表
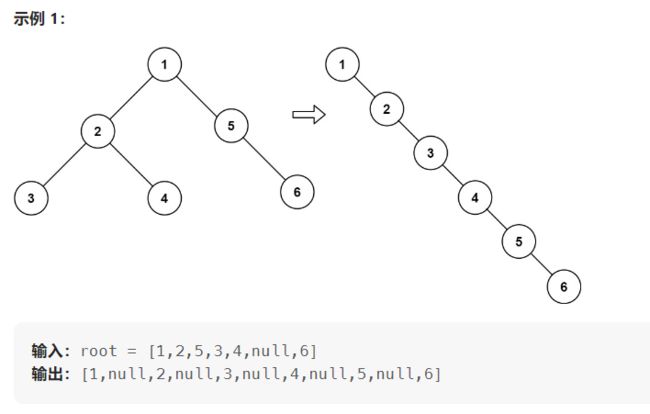
114. 二叉树展开为链表
给你二叉树的根结点 root ,请你将它展开为一个单链表:
- 展开后的单链表应该同样使用
TreeNode,其中right子指针指向链表中下一个结点,而左子指针始终为null。
展开后的单链表应该与二叉树 先序遍历 顺序相同。
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, x):
# self.val = x
# self.left = None
# self.right = None
class Solution:
def flatten(self, root):
while root:
if root.left: #左子树存在的话才进行操作
sub_left = root.left
while sub_left.right: #左子树的右子树找到最深
sub_left = sub_left.right
sub_left.right = root.right #将root的右子树挂到左子树的右子树的最深
root.right = root.left #将root的左子树挂到右子树
root.left = None #将root左子树清空
root = root.right #继续下一个节点的操作
222.完全二叉树的节点个数
222. 完全二叉树的节点个数
给你一棵 完全二叉树 的根节点 root ,求出该树的节点个数。
完全二叉树 的定义如下:在完全二叉树中,除了最底层节点可能没填满外,其余每层节点数都达到最大值,并且最下面一层的节点都集中在该层最左边的若干位置。若最底层为第 h 层,则该层包含 1~ 2h 个节点。
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def countNodes(self, root: Optional[TreeNode]) -> int:
if root is None:
return 0
ans = 0
cur = [root]
while cur:
vals = []
nxt = []
for node in cur:
ans+=1
if node.left: nxt.append(node.left)
if node.right: nxt.append(node.right)
cur = nxt
ans+=len(vals)
return ans236.二叉树的最近公共祖先
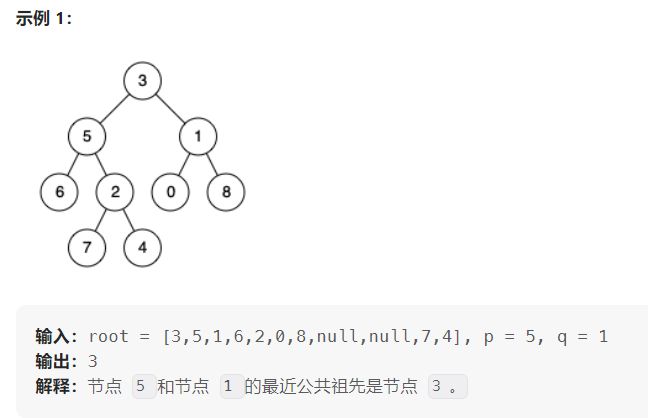
236. 二叉树的最近公共祖先
给定一个二叉树, 找到该树中两个指定节点的最近公共祖先。
百度百科中最近公共祖先的定义为:“对于有根树 T 的两个节点 p、q,最近公共祖先表示为一个节点 x,满足 x 是 p、q 的祖先且 x 的深度尽可能大(一个节点也可以是它自己的祖先)。”
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, x):
# self.val = x
# self.left = None
# self.right = None
class Solution:
def lowestCommonAncestor(self, root: 'TreeNode', p: 'TreeNode', q: 'TreeNode') -> 'TreeNode':
if root in (None, p, q):
return root
left = self.lowestCommonAncestor(root.left, p, q)
right = self.lowestCommonAncestor(root.right, p, q)
if left and right:
return root
return left if left else right