数据结构和算法——归并排序（有序子列的归并、递归算法、非递归算法、思路图解、C语言代码）

目录

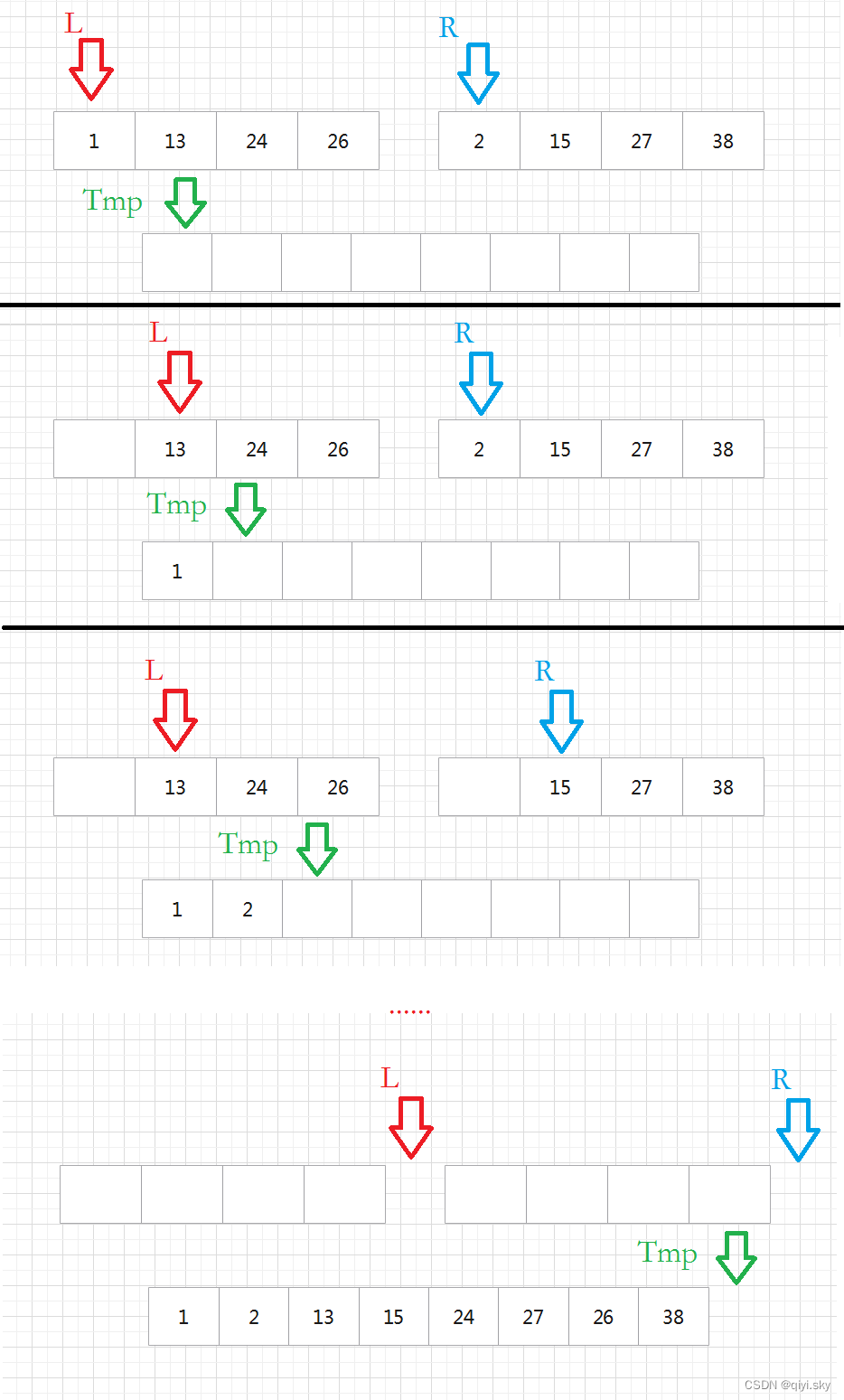
有序子列的归并

思路图解

代码（C语言）

时间复杂度

递归算法

代码（C语言）

图示

时间复杂度

统一函数接口

非递归算法

图示

代码（C语言） 

统一函数接口

---

有序子列的归并

思路图解

代码（C语言）

/* L = 左边起始位置, R = 右边起始位置, RightEnd = 右边终点位置*/
void Merge( ElementType A[], ElementType TmpA[], int L, int R, int RightEnd )
{ /* 将有序的A[L]~A[R-1]和A[R]~A[RightEnd]归并成一个有序序列 */
     int LeftEnd, NumElements, Tmp;
     int i;
     
     LeftEnd = R - 1; /* 左边终点位置 */
     Tmp = L;         /* 有序序列的起始位置 */
     NumElements = RightEnd - L + 1;
     
     while( L <= LeftEnd && R <= RightEnd ) {
         if ( A[L] <= A[R] )
             TmpA[Tmp++] = A[L++]; /* 将左边元素复制到TmpA */
         else
             TmpA[Tmp++] = A[R++]; /* 将右边元素复制到TmpA */
     }

     while( L <= LeftEnd )
         TmpA[Tmp++] = A[L++]; /* 直接复制左边剩下的 */
     while( R <= RightEnd )
         TmpA[Tmp++] = A[R++]; /* 直接复制右边剩下的 */
         
     for( i = 0; i < NumElements; i++, RightEnd -- )
         A[RightEnd] = TmpA[RightEnd]; /* 将有序的TmpA[]复制回A[] */
}

时间复杂度

如果两个子列一共有N个元素，则归并的时间复杂度为：

递归算法

代码（C语言）

void Msort( ElementType A[], ElementType TmpA[], int L, int RightEnd )
{ /* 核心递归排序函数 */ 
     int Center;
     
     if ( L < RightEnd ) {
          Center = (L+RightEnd) / 2;
          Msort( A, TmpA, L, Center );              /* 递归解决左边 */ 
          Msort( A, TmpA, Center+1, RightEnd );     /* 递归解决右边 */  
          Merge( A, TmpA, L, Center+1, RightEnd );  /* 合并两段有序序列 */ 
     }
}

图示

时间复杂度

统一函数接口

void Merge_Sort(ElementType A[],int N)
{
    ElementType *TmpA;
    TmpA = malloc( N * sizeof(ElementType) );
    if(TmpA != NULL)
    {
        MSort(A,TmpA,0,N-1);
        free(TmpA);
    }
    else    Error("空间不足");
}

如果只在Merge中声明临时数组TmpA，则在递归的过程中会不断进行申请和释放空间；原本只需要一块空间的情况则会变成以下的情况：

非递归算法

图示

代码（C语言） 

/* 这里Merge函数在递归版本中给出 */

/* length = 当前有序子列的长度*/
void Merge_pass( ElementType A[], ElementType TmpA[], int N, int length )
{ /* 两两归并相邻有序子列 */
     int i, j;
      
     for ( i=0; i <= N-2*length; i += 2*length )
         Merge( A, TmpA, i, i+length, i+2*length-1 );
     if ( i+length < N ) /* 归并最后2个子列*/
         Merge( A, TmpA, i, i+length, N-1);
     else /* 最后只剩1个子列*/
         for ( j = i; j < N; j++ ) TmpA[j] = A[j];
}

统一函数接口

void Merge_Sort( ElementType A[], int N )
{ 
     int length; 
     ElementType *TmpA;
     
     length = 1; /* 初始化子序列长度*/
     TmpA = malloc( N * sizeof( ElementType ) );
     if ( TmpA != NULL ) {
          while( length < N ) {
              Merge_pass( A, TmpA, N, length );
              length *= 2;
              Merge_pass( TmpA, A, N, length );
              length *= 2;
          }
          free( TmpA );
     }
     else printf( "空间不足" );
}

注意：归并排序一般不用于内排序，因为其要额外消耗空间；所以一般在外排序时才会使用归并排序。

---

end

---

学习自：MOOC数据结构——陈越、何钦铭