蓝桥杯15届第九题——垒骰子（dfs、动态规划、矩阵）

前言：该题很值得研究，为什么这么说呢？
题目考查了较多方面的知识点，相信如果将这道题完全理解的话，我们对考查的知识点应用起来会更加得心应手。
下面我会通过三种方式将题目解析透彻，从浅入深。

垒骰子题目

赌圣atm晚年迷恋上了垒骰子，就是把骰子一个垒在另一个上边，不能歪歪扭扭，要垒成方柱体。
经过长期观察，atm 发现了稳定骰子的奥秘：有些数字的面贴着会互相排斥！
我们先来规范一下骰子：1 的对面是 4，2 的对面是 5，3 的对面是 6。
假设有 m 组互斥现象，每组中的那两个数字的面紧贴在一起，骰子就不能稳定的垒起来。 atm想计算一下有多少种不同的可能的垒骰子方式。
两种垒骰子方式相同，当且仅当这两种方式中对应高度的骰子的对应数字的朝向都相同。
由于方案数可能过多，请输出模 10⁹ + 7 的结果。
不要小看了 atm 的骰子数量哦～
「输入格式」
第一行两个整数 n m
n表示骰子数目
接下来 m 行，每行两个整数 a b ，表示 a 和 b 不能紧贴在一起。
「输出格式」
一行一个数，表示答案模 10⁹ + 7 的结果。
「样例输入」
2 1
1 2
「样例输出」
544
对于 30% 的数据：n <= 5
对于 60% 的数据：n <= 100
对于 100% 的数据：0 < n <= 10⁹, m <= 36

---

三种方法的初始化条件：
①、创建hc二维数组：判断骰子面与骰子面之间是否互斥。
例如：1与2排斥
对应hc数组： hc[1][2]=true hc[2][1]=true

②、创建op数组：将骰子对应面配对。
例如：（题目中有提示）骰子上1的对面为4
对应op数组：op[1]=4 op[4]=1

注意：两种垒骰子方式相同，当且仅当这两种方式中对应高度的骰子的对应数字的朝向都相同，所以一个垒好的骰子柱，每个骰子都能转4次，表示不同方案。

---

一：dfs解题

dfs方式解题较好理解，主要是通过递归枚举的方式将符合条件的垒骰子方式，累加起来，最后再乘以4ⁿ即可。

#include
#define ll long long
const ll MOD=1e9+7;
ll n, m, sum=0;
using namespace std;
//骰子对应面
int op[7];
bool hc[7][7]={false};
void init(void)
{
	op[1]=4;
	op[4]=1;
	op[2]=5;
	op[5]=2;
	op[3]=6;
	op[6]=3;
} 

ll dfs(int up, ll cnt)
{
	if(cnt==0) return 1;
	ll ans=0;
	for(int down=1; down<=6; down++)
	{
		if(hc[up][down]) continue;	//排除互斥的面 
		ans = (ans + dfs(op[down], cnt-1))%MOD;
	}
	return ans;
}

int main()
{
	init();
	cin>>n>>m;
//	互斥面 
	for(int i=0; i<m; i++)
	{
		int a, b;
		cin>>a>>b;
		hc[a][b]=true;
		hc[b][a]=true;
	}
	
//	dfs递归，第一个骰子可以任意放，没有限制
	for(int down=1; down<=6; down++)			//down:朝下的数字
	{
		sum=(sum + dfs(op[down], n-1))%MOD;		//op[down]:朝上的数字 
	} 											//cnt:未垒的骰子数 
	
//	4的快速幂 
	ll ans4=0;
	ll temp=4;
	ll p=n;  
	while(p!=0)
	{
		if(p&1) ans4 = (ans4 + temp)%MOD;
		temp = (temp * temp)%MOD;
		p >>= 1;
	}
	
//	累乘
/*	ll ans4=1;
	for(int i=0; i
	
	cout<<(sum*ans4)%MOD;
	return 0;
}

在这种解题方式上用快速幂有些多余。分枝过多的递归当n=100时，几乎不能在题目规定时间内计算出来。当n<100时，通过累乘的方式将4一次、一次乘给ans，这并不会对程序的效率造成很大影响。

---

二：动态规划

为了方便我们理解如何在该题运用动态规划，我提供了数据图、模拟图。
图中枚举了少量示例在动态规划中的变化。

模拟图

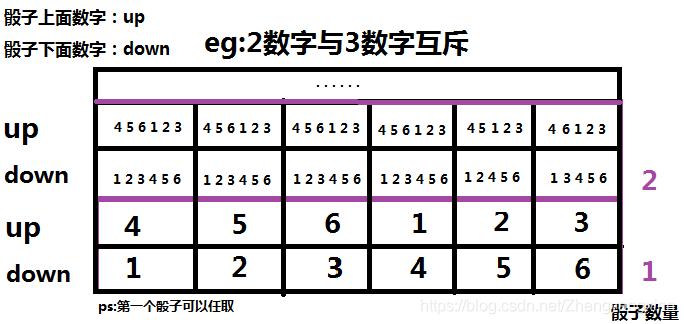
在模拟图可以看到，我们可以将垒骰子不同情况根据初始化朝下的面不同均分成6份，最后将6种情况递推结果相加得到全部不同垒骰子情况。（这里不考虑转面的情况，下面统一用快速幂即可完成）。
图中当垒第一个骰子的时候朝下的面可以取任何一个数字。

//	初始化dp：第一个骰子可以任意放  
	for(int i=0; i<7; i++)
	dp[1][i]=1;

当垒第二个骰子时，就要考虑互斥的情况，将互斥的情况排除。
依次类推出垒下一个骰子的不同情况。

数据图

图中清晰得表明了dp[k]与dp[k-1]之间的关系：
dp[k][down] = ∑dp[k-1][down1]（其中down与op[down1]不冲突）
up：垒好骰子朝上的数字。
down：垒好骰子朝下的数字。
down1：将要垒的骰子朝下的数字。
解题路径：
①、确定已垒好的骰子朝上的面数字up。
②、枚举down1（1~6）判断与up是否互斥。
③、将与up不冲突的dp[k-1][down1]累加给dp[k][down]。
④、k递增，重复①~④步骤，直到k等于n。
⑤、累加dp[n][down]（1~6）得到sum
⑥、用快速幂算出4ⁿ。
⑦、将sum乘以4ⁿ输出结果。

//动态规划代码
#include
#define ll long long
using namespace std;
ll op[7], n, m, sum=0;
bool hc[7][7]={false};
ll dp[150][7];
const ll MOD = 1e9+7;
void init(void)
{
	op[1]=4;
	op[4]=1;
	op[2]=5;
	op[5]=2;
	op[3]=6;
	op[6]=3;
}

int main()
{
	init();
	cin>>n>>m;
	
	memset(dp, 0, sizeof(dp));
	for(int i=0; i<m; i++)
	{
		int a, b;
		cin>>a>>b;
		hc[a][b]=true;
		hc[b][a]=true;
	}
	
//	初始化dp：第一个骰子可以任意放  
	for(int i=0; i<7; i++)
	dp[1][i]=1;
	
	//从第二个骰子开始递推 
	for(int k=2; k<=n; k++)				//k:  垒骰子数 
	{
		for(int down=1; down<7; down++)		//down：垒好骰子朝下的数字 
		{
			for(int down1=1; down1<7; down1++)		//down1：尝试垒骰子朝下的数字
			{ 
//				判断尝试垒骰子朝下的数字与垒好骰子朝上的数字是否互斥
				if(hc[op[down]][down1]) continue;	
				dp[k][down]=(dp[k][down]+dp[k-1][down1])%MOD;
			}
//			cout<
		}
//		cout<
	} 
	
//	统计所有方案数 
	for(int i=1; i<7; i++)
	sum=(sum+dp[n][i])%MOD;
	
//	4的快速幂
 	ll p=n;
	ll ans=0;
	ll temp=4;
	while(p!=0)
	{
		if(p&1) ans=(ans+temp)%MOD;
		temp = (temp * temp)%MOD;
		p >>= 1;
	} 
	cout<<(ans*sum)%MOD;
	
	return 0;
}

三、矩阵

上述动态分析方法为什么会出现超时的情况呢？
在上面dp数组动态变化的时候，递推次数过多，时间复杂度太大。
这时我们可以通过引入矩阵： 实现 “ 加法 ” 变 “ 乘法 ” 。
当“加法”转换为“乘法”后，快速幂即可得出方案数（未考虑转面情况）。

构建计算工具：
1、初始化数组：当垒第一个骰子的时候朝上的面可以取任何一个数字。

2、在动态规划中，dp [ k ] [ j ] = ∑dp [ k - 1 ] [ i ]（其中j与op[i]不冲突）
temp矩阵作用：实现 选择 垒骰子功能。

3、ans数组：temp矩阵^n-1 * 初始化数组 = ans数组
ans数组的值类似于动态规划中的dp[n]。

举例：图中模拟的是2数字与3数字互斥，骰子数量为2的情况。

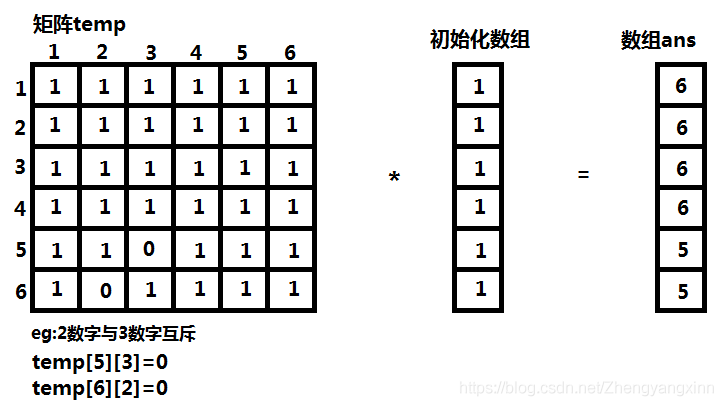
解题路径：
①、初始化数组。
②、构建temp矩阵。
③、计算temp^n-1 * 初始化数组，得到ans数组。
④、将ans数组累加得到sum。
⑤、4的快速幂得到4ⁿ。
⑥、输出结果：sum * 4ⁿ。

//矩阵
#include
#define ll long long
const ll MOD = 1e9+7; 
using namespace std;
ll op[7], n, m, sum=0;
bool hc[7][7]={false};

struct M{
	ll a[7][7];
	ll b[7];
};

void init(void)
{
	op[1]=4;
	op[4]=1;
	op[2]=5;
	op[5]=2;
	op[3]=6;
	op[6]=3;
}

M cf(M a, M b)
{
	M c;
	memset(c.a, 0, sizeof(c.a));
	for(int i=1; i<7; i++)
	for(int j=1; j<7; j++)
	for(int k=1; k<7; k++)
		c.a[i][j]=(c.a[i][j]+(a.a[i][k]*b.a[k][j])%MOD)%MOD;
	return c;
}

M cf1(M a, M dw)
{
	M ans;
	for(int i=1; i<7; i++)
	ans.b[i]=0;
	for(int i=1; i<7; i++)
	for(int j=1; j<7; j++)
		ans.b[i]=(ans.b[i]+(a.a[i][j]*dw.b[j])%MOD)%MOD;
	return ans;
}


int main()
{
	init();
	cin>>n>>m;
	M temp, ans;
	for(int i=1; i<7; i++)
	for(int j=1; j<7; j++)
	temp.a[i][j]=1;
	for(int i=0; i<m; i++)
	{
		int a, b;
		cin>>a>>b;
		temp.a[op[a]][b]=0;		// 矩阵下标统一为朝上数字
		temp.a[op[b]][a]=0;		// temp.a[x][y]:x与y表示两个骰子朝上的数字
	}
	
/*	for(int i=1; i<7; i++)
	{
		for(int j=1; j<7; j++)
		cout<	
	
//	M快速幂
	ll p=n-1; 
//	初始化 
	for(int i=1; i<7; i++)
		ans.b[i]=1;

	while(p!=0)
	{
		if(p&1) ans=cf1(temp,ans);	//矩阵 * 列 
		temp=cf(temp,temp);
		p>>=1;
	}
/*	for(int i=1; i<7; i++)
	cout<
	for(int i=1; i<7; i++)
	sum = (sum + ans.b[i])%MOD;

//	4快速幂 
	p=n;
	ll a=0;
	ll temp1=4;
	while(p!=0)
	{
		if(p&1) a=(temp1+a)%MOD;
		temp1=(temp1*temp1)%MOD;
		p>>=1;
	}
	cout<<(sum*a)%MOD;
	
	return 0;
}

希望能够将自己的一些学习经验分享给有需要的人。
我是小郑，一个坚持不懈的小白。