深度优先搜索(BFS)与广度优先搜索(DFS)

---

前言

本次撰写的内容是深度优先搜索与广度优先搜索
这两三天将会对前几天学习的东西进行一个总结，之后开始写学生管理系统，如果有空闲时间将会继续写周报。

---

一、深度优先搜索

1.定义

DFS（Depth-First Search）：深度优先搜索属于图算法的一种，其过程简要来说是对每一个可能的分支路径深入到不能再深入为止，而且每个节点只能访问一次。

2.关键

深度优先搜索其实是围绕着一词“回溯”展开，我们若是理解了回溯，那么对理解深度优先有十分大的帮助。

因为DFS是一种关于图的算法，所以我们从图的角度展开理解，回溯对于图来说，就相当于对已经走过的路进行新的尝试。

3.文字理解

首先因为DFS是一种关于图的算法，所以笔者在此用文字对其进行简单的描述，后文会通过图片来进一步理解。

深度优先搜索的步骤分为 1.递归下去 2.回溯上来。顾名思义，深度优先，则是以深度为准则，先一条路走到底，直到达到目标。这里称之为递归下去。

否则既没有达到目标又无路可走了，那么则退回到上一步的状态，走其他路。这便是回溯上来

4.图片理解

在此笔者贴出几张丑陋的图片供读者理解。以下是迷宫中一个人运用DFS走到终点的路径：

1.首先向右走

2.其次打叉的地方是障碍物，我们走不通，呢么根据方向顺序我们需要尝试向下走，走通了，那么我们可以向下走

3.然后我们继续尝试向右

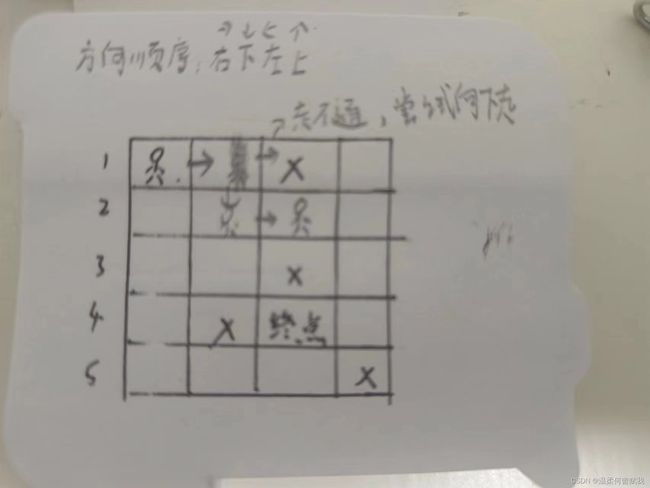
4.最后我们一次类推走到终点

但是我们显然还要尝试别的走法，那么我们就需要退回去继续尝试，那么这里就要用到我们回溯的思想了

例如我们回溯到下面这步，我们在没回溯此步之前是向下走的，那么我们按照顺序就需要依次尝试向左与向上了，左边是障碍物，上面是我们已经走过的路，那么四个方向都不能走时，我们就需要继续回溯。

在这里有些小伙伴可能会问了，怎么知道我们已经走过哪些路了呢，那么就需要我们额外设立一个数组进行记录，如果下一步要走的路已经在我们记录的路中，那么我们就不会走这一步，同时，当我们回溯到上一步时，也会将数组中此步的坐标删除。

5.例题1

我们常常使用深度优先搜索解决迷宫问题，那么我们就以我上面的图为迷宫的原型，问小人走到终点所需的最短步数。

6.例题1代码

在此代码笔者运用了递归的方法，其实用栈也可以实现，因为栈的本质其实就是递归。学习c++后笔者将会考虑补上栈法的代码

# include 

int n, m, p, q;
int min = 888888;
int a[51][51], book[51][51];

//深度优先搜索就是一步步走到底，那么每一步都要尝试上下左右，
//如果第一次向右可以通过那么就进行到下一步，继续按照上下左右寻找，找到可以走的路就继续无路可走或已在路径中就返回

void dfs(int x, int y, int step)
{
	int next[4][2] = { {0,1},{1,0}, {0,-1}, {-1,0} };//顺序是右，下，左，上。

	int tx, ty, k;
	//判断是否到达指定位置
	if (x == p && y == q)
	{
		//更新最小值
		if (step < min)
			min = step;
		return;//请注意这里的返回很重要
		//走到目的地后返回，然后尝试下一个方向。
		//因为我们需要尝试四个方向，所以要需要回溯。
	}

	//枚举四种写法
	for (k = 0; k < 4; k++)
	{
		//计算下一个点的坐标
		tx = x + next[k][0];
		ty = y + next[k][1];

		//判断是否越界
		if (tx<1 || tx>n || ty<1 || ty>m)
			continue;
		//判断该点是否为障碍物或者已经在路径中，已经在路径中就不用重复尝试了
		if (a[tx][ty] == 0 && book[tx][ty] == 0)//等于0就证明可以尝试这个方向
		{
			book[tx][ty] = 1;
			dfs(tx, ty, step + 1);//使用递归开始尝试下一个点的方向。
			book[tx][ty] = 0;//这里就是深度优先搜索的核心回溯，取消上一个点的标记，就像上一个扑克牌算法取走扑克牌一样
		}
	}
	
	return;
}

int main()
{
	int j, i, startX, startY;
	scanf_s("%d %d", &n, &m);//输入迷宫有多少行多少列
	printf("读入迷宫\n");
	for (i = 1; i <= n; ++i)//读入迷宫
		for (j = 1; j <= m; ++j)
			scanf_s("%d", &a[i][j]);//记得i与j的值就是最小值， 起始位置坐标不能小于i与j
	printf("\n");
	printf("读入起点和终点坐标");
	scanf_s("%d %d %d %d", &startX, &startY, &p, &q);

	//从起点开始搜索
	book[startX][startY] = 1;
	//第一个是起始x，第二个是起始y， 初始步数为0
	dfs(startX, startY, 0);
	//打印最短步数。
	printf("%d", min);
	return 0;

}

输入：
5 4 （迷宫行列）
（迷宫地图，1代表障碍物，0代表可以走）
0 0 1 0
0 0 0 0
0 0 1 0
0 1 0 0
0 0 0 1
1 1 4 3（分别为起点与终点坐标）
输出：
7

7.例题2

我们以此道例题为例，不过我们将3个盒子变为9个盒子

8.例题2理解

我们将手中空闲的牌按顺序放入盒子中，当放完后便走回上一个盒子取回原来的牌，然后继续按照顺序放入，手中牌放完后就输出盒子中牌的序列

9.例题2代码

# include 
# include 
//深度优先算法的关键在于回溯
//用递归实现
int a[10], book[10], n;

void dfs(int step)//step表示现在站在第几个盒子面前
{
	int i;
	if (step == n + 1)//当面前没有盒子时，则输出序列
	{
		for (i = 1; i <= n; ++i)
			printf("%d", a[i]);
		printf("\n");

		return;//返回之前一步，就是上一步递归的语句

	}

	//此时站在第step个盒子面前，应该放哪张牌呢？
	//按照1，2，3.....n的顺序一一尝试
	for (i = 1; i <= n; i++)
	{
		//首先判断扑克牌是否还在手上，用book数组标记，0就代表不在手上，1就代表在手上
		if (book[i] == 0)
		{
			a[step] = i;//将扑克牌放入盒子里
			book[i] = 1; //标记此牌已经不在手上了

			//下一步就该移动到下一个盒子了
			dfs(step + 1); //要想实现回溯，可以利用栈的先入后出特性，也可以采用递归的方式（因为递归本身就是基于方法调用栈来实现
			book[i] = 0;//因为关键是回溯，所以需要当牌放完后要将刚才尝试的牌取出。
		}
	}
	return;
}

int main()
{
	scanf_s("%d", &n);
	dfs(1);
	return 0;
}

二、广度优先搜索

1.定义

广度优先搜索较之深度优先搜索之不同在于，深度优先搜索旨在不管有多少条岔路，先一条路走到底，不成功就返回上一个路口然后就选择下一条岔路，而广度优先搜索旨在面临一个路口时，把所有的岔路口都记下来，然后选择其中一个进入，然后将它的分路情况记录下来，然后再返回来进入另外一个岔路，并重复这样的操作，用图形来表示则是这样的

2.关键

广度优先搜索关键在于重放，回放是继续遍历先前已经遍历过的结点 。

3.文字理解

广度优先搜索的方式是使用队列，运用重放的方法进行出对入队的操作从而达到目的。
就是对下一步能走通的位置进行入队，已经重放完毕的位置进行出队。

4.例题

深度优先搜索与广度优先搜索都可用于迷宫问题，那么我们依然用迷宫问题作为例题

5.例题代码

# include 
# include 
struct node
{
	int x;
	int y;
	int step;

};

int main()
{
	int m, n;
	int head, tail;
	int lp, lq;
	int a[51][51] = { 0 };//迷宫内的0和1
	int tx, ty;
	
	scanf_s("%d %d", &n, &m);//输入迷宫有多少行多少列
	printf("读入迷宫\n");
	for (int i = 1; i <= n; ++i)//读入迷宫
		for (int j = 1; j <= m; ++j)
			scanf_s("%d", &a[i][j]);//记得i与j的值就是最小值， 起始位置坐标不能小于i与j
	printf("\n");
	printf("读入起点和终点坐标");
	scanf_s("%d %d",  &lp, &lq);


	struct node q[2501];//设置队列的容量
	int next[4][2] = { {0,1},{-1,0},{0,- 1},{1,0} };
	int book[51][51] = { 0 };//初始化存储数组
	head = tail = 1;
	q[tail].x = 1;//起点横坐标；
	q[tail].y = 1;//起点纵坐标；
	q[tail].step = 0;//步数刚开始没走
	tail++;//队列尾部移动
	book[1][1] = 1;
	int flag = 0;//表示是否到达终点
	
	while (head < tail)//当队列不为空时循环
	{
		for (int i = 0; i < 4; i++)//枚举四个方向
		{
			tx = q[head].x + next[i][0];//计算下一个点的坐标，记得是head
			ty = q[head].y + next[i][1];
			if (tx<1 || tx>n || ty<1 || ty>m)
				continue;//判断越界哩
			if (book[tx][ty] == 0 && a[tx][ty] == 0)//不为障碍物且不为已经走过的路
			{
				book[tx][ty] = 1;
				q[tail].x = tx;
				q[tail].y = ty;
				q[tail].step = q[head].step + 1;//步数是重放的步数+1
				tail++;
			}
			if (tx == lp && ty == lq)//终点坐标
			{
				flag = 1;
				break;
			}
		}
		if (flag == 1)
			break;
		head++;//把已经重放的点去除
	}

	printf("%d", q[tail-1].step);
	return 0;

}

总结

深度优先搜索的关键在于回溯与递归（栈）
广度优先搜索的关键在于重放与队列
这两种方法常用于迷宫问题，其实他们的原理并不难，最重要是我们能够理解算法的步骤并对之加深印象