8、动手学深度学习——现代卷积神经网络:AlexNet
1、学习表征
在2012年前,图像特征都是机械地计算出来的。事实上,设计一套新的特征函数、改进结果,并撰写论文是盛极一时的潮流
另一组研究人员,包括Yann LeCun、Geoff Hinton、Yoshua Bengio、Andrew Ng、Shun ichi Amari和Juergen Schmidhuber,想法则与众不同:他们认为特征本身应该被学习。 此外,他们还认为,在合理地复杂性前提下,特征应该由多个共同学习的神经网络层组成,每个层都有可学习的参数。在机器视觉中,最底层可能检测边缘、颜色和纹理。事实上,Alex Krizhevsky、Ilya Sutskever和Geoff Hinton提出了一种新的卷积神经网络变体AlexNet。有趣的是,在网络的最底层,模型学习到了一些类似于传统滤波器的特征抽取器。下图时是从AlexNet论文 (Krizhevsky et al., 2012)复制的,描述了底层图像特征。

AlexNet的更高层建立在这些底层表示的基础上,以表示更大的特征,如眼睛、鼻子、草叶等等。而更高的层可以检测整个物体,如人、飞机、狗或飞盘。最终的隐藏神经元可以学习图像的综合表示,从而使属于不同类别的数据易于区分。尽管一直有一群执着的研究者不断钻研,试图学习视觉数据的逐级表征,然而很长一段时间里这些尝试都未有突破。深度卷积神经网络的突破出现在2012年。突破可归因于两个关键因素,即数据量的积累和硬件计算能力的提升。
2、概述
AlexNet中神经网络有6000万个参数和650,000个神经元,由五个卷积层组成,其中一些层后面是最大池层,还有三个全连接层,最后是1000路softmax。为了使训练更快,我们使用了非饱和神经元和非常有效的卷积运算GPU实现。为了减少全连接层中的过度拟合,我们采用了一种最近开发的正则化方法,称为“dropout”,该方法被证明非常有效。
3、数据集
1. 基础数据集
ImageNet是一个包含超过1500万个标记的高分辨率图像的数据集,属于大约22,000个类别。ImageNet由可变分辨率的图像组成,而我们的系统需要恒定的输入维度。因此,我们将图像下采样到256 × 256的固定分辨率。给定一个矩形图像,我们首先重新缩放图像,使短边的长度为256,然后从结果图像中裁剪出中心的256×256块。我们没有以任何其他方式对图像进行预处理,除了从每个像素中减去训练集上的平均活动。因此,我们在像素的(居中的)原始RGB值上训练了我们的网络。
2. 数据增强
AlexNet在训练时增加了大量的图像增强数据,如翻转、裁切和变色。 这使得模型更健壮,更大的样本量有效地减少了过拟合。 减少图像数据上的过拟合的最简单和最常见的方法是使用标签保留变换(例如,[25、4、5])。论文中采用了两种不同形式的数据增强,这两种方法都允许变换后的图像从原始图像产生,计算量很小,所以变换后的图像不需要存储在磁盘上。在实现中,转换后的图像在CPU上以Python代码生成,而GPU则在前一批图像上进行训练。因此,这些数据增强方案实际上是计算自由的。第一种形式的数据增强包括生成图像平移和水平反射。第二种形式的数据增强包括改变训练图像中RGB通道的强度。
4、网络架构
AlexNet和LeNet的架构非常相似,如下图所示。 注意,本节中提供的是一个稍微精简版本的AlexNet,去除了当年需要两个小型GPU同时运算的设计特点。
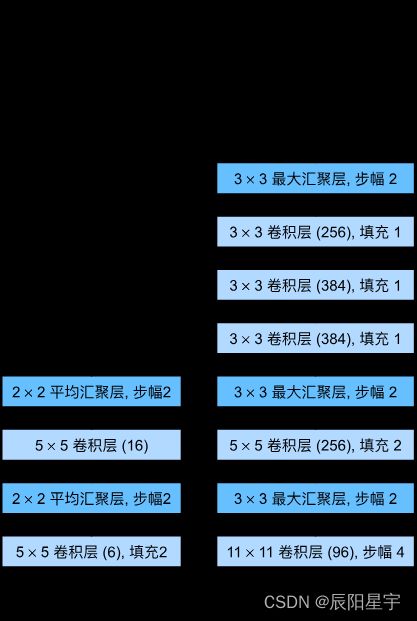
AlexNet和LeNet的设计理念非常相似,但也存在显著差异。AlexNet比相对较小的LeNet5要深得多。AlexNet由八层组成:五个卷积层、两个全连接隐藏层和一个全连接输出层。
- AlexNet使用ReLU而不是sigmoid作为其激活函数。
- 下面的内容将深入研究AlexNet的细节。
1. 模型设计
在AlexNet的第一层,卷积窗口的形状是11x11。 由于ImageNet中大多数图像的宽和高比MNIST图像的多10倍以上,因此,需要一个更大的卷积窗口来捕获目标。 第二层中的卷积窗口形状被缩减为5x5,然后是3x3。 此外,在第一层、第二层和第五层卷积层之后,加入窗口形状为3x3、步幅为2的最大汇聚层。 而且,AlexNet的卷积通道数目是LeNet的10倍。
在最后一个卷积层后有两个全连接层,分别有4096个输出。 这两个巨大的全连接层拥有将近1GB的模型参数。 由于早期GPU显存有限,原版的AlexNet采用了双数据流设计,使得每个GPU只负责存储和计算模型的一半参数。 幸运的是,现在GPU显存相对充裕,所以现在很少需要跨GPU分解模型(因此,本书的AlexNet模型在这方面与原始论文稍有不同)。
2. 激活函数
AlexNet将sigmoid激活函数改为更简单的ReLU激活函数。 一方面,ReLU激活函数的计算更简单,它不需要如sigmoid激活函数那般复杂的求幂运算。 另一方面,当使用不同的参数初始化方法时,ReLU激活函数使训练模型更加容易。 当sigmoid激活函数的输出非常接近于0或1时,这些区域的梯度几乎为0(梯度消失),因此反向传播无法继续更新一些模型参数。 相反,ReLU激活函数在正区间的梯度总是1。 因此,如果模型参数没有正确初始化,sigmoid函数可能在正区间内得到几乎为0的梯度,从而使模型无法得到有效的训练。
在梯度下降的训练时间方面,饱和非线性函数(sigmoid)比非饱和非线性(ReLU)慢得多。使用ReLU的深度卷积神经网络的训练速度比使用tanh单元的快几倍。
3. 重叠池化层
CNN中的池化层总结了同一内核映射中相邻神经元组的输出。传统上,由相邻池化单元汇总的邻域不重叠(例如,[17,11,4])。更准确地说,池化层可以被认为是由间隔s个像素的池化单元组成的网格,每个池化单元总结了以池化单元的位置为中心的大小为z × z的邻域。如果我们设置s = z(步幅为s,池化核的尺寸为z),我们获得了CNN中常用的传统局部池。如果我们设置s < z,则我们获得重叠池化。这就是我们在整个网络中使用的,s = 2,z = 3。与产生相等尺寸的输出的非重叠方案s = 2,z = 2相比,该方案将前1和前5错误率分别降低了0.4%和0.3%。我们通常在训练过程中观察到,具有重叠池的模型更不容易会过拟合。
4. 丢弃法Dropout
AlexNet通过暂退法( 4.6节)控制全连接层的模型复杂度,而LeNet只使用了权重衰减。 最近引入的技术,称为“dropout”,包括将每个隐藏神经元的输出设置为零,概率为0.5。
5、代码
1. 模型
import torch
from torch import nn
from d2l import torch as d2l
net = nn.Sequential(
# 这里使用一个11*11的更大窗口来捕捉对象。
# 同时,步幅为4,以减少输出的高度和宽度。
# 另外,输出通道的数目远大于LeNet
nn.Conv2d(1, 96, kernel_size=11, stride=4, padding=1), nn.ReLU(),
nn.MaxPool2d(kernel_size=3, stride=2),
# 减小卷积窗口,使用填充为2来使得输入与输出的高和宽一致,且增大输出通道数
nn.Conv2d(96, 256, kernel_size=5, padding=2), nn.ReLU(),
nn.MaxPool2d(kernel_size=3, stride=2),
# 使用三个连续的卷积层和较小的卷积窗口。
# 除了最后的卷积层,输出通道的数量进一步增加。
# 在前两个卷积层之后,汇聚层不用于减少输入的高度和宽度
nn.Conv2d(256, 384, kernel_size=3, padding=1), nn.ReLU(),
nn.Conv2d(384, 384, kernel_size=3, padding=1), nn.ReLU(),
nn.Conv2d(384, 256, kernel_size=3, padding=1), nn.ReLU(),
nn.MaxPool2d(kernel_size=3, stride=2),
nn.Flatten(),
# 这里,全连接层的输出数量是LeNet中的好几倍。使用dropout层来减轻过拟合
nn.Linear(6400, 4096), nn.ReLU(),
nn.Dropout(p=0.5),
nn.Linear(4096, 4096), nn.ReLU(),
nn.Dropout(p=0.5),
# 最后是输出层。由于这里使用Fashion-MNIST,所以用类别数为10,而非论文中的1000
nn.Linear(4096, 10))
我们构造一个高度和宽度都为224的单通道数据,来观察每一层输出的形状。
X = torch.randn(1, 1, 224, 224)
for layer in net:
X=layer(X)
print(layer.__class__.__name__,'output shape:\t',X.shape)
Conv2d output shape: torch.Size([1, 96, 54, 54])
ReLU output shape: torch.Size([1, 96, 54, 54])
MaxPool2d output shape: torch.Size([1, 96, 26, 26])
Conv2d output shape: torch.Size([1, 256, 26, 26])
ReLU output shape: torch.Size([1, 256, 26, 26])
MaxPool2d output shape: torch.Size([1, 256, 12, 12])
Conv2d output shape: torch.Size([1, 384, 12, 12])
ReLU output shape: torch.Size([1, 384, 12, 12])
Conv2d output shape: torch.Size([1, 384, 12, 12])
ReLU output shape: torch.Size([1, 384, 12, 12])
Conv2d output shape: torch.Size([1, 256, 12, 12])
ReLU output shape: torch.Size([1, 256, 12, 12])
MaxPool2d output shape: torch.Size([1, 256, 5, 5])
Flatten output shape: torch.Size([1, 6400])
Linear output shape: torch.Size([1, 4096])
ReLU output shape: torch.Size([1, 4096])
Dropout output shape: torch.Size([1, 4096])
Linear output shape: torch.Size([1, 4096])
ReLU output shape: torch.Size([1, 4096])
Dropout output shape: torch.Size([1, 4096])
Linear output shape: torch.Size([1, 10])
2. 读取数据集
尽管原文中AlexNet是在ImageNet上进行训练的,但本书在这里使用的是Fashion-MNIST数据集。因为即使在现代GPU上,训练ImageNet模型,同时使其收敛可能需要数小时或数天的时间。 将AlexNet直接应用于Fashion-MNIST的一个问题是,Fashion-MNIST图像的分辨率(像素)低于ImageNet图像。 为了解决这个问题,我们将它们增加到(通常来讲这不是一个明智的做法,但在这里这样做是为了有效使用AlexNet架构)。 这里需要使用d2l.load_data_fashion_mnist函数中的resize参数执行此调整
batch_size = 128
train_iter, test_iter = d2l.load_data_fashion_mnist(batch_size, resize=224)
3. 训练
lr, num_epochs = 0.01, 10
d2l.train_ch6(net, train_iter, test_iter, num_epochs, lr, d2l.try_gpu())
参考文章:7.1. 深度卷积神经网络(AlexNet)、AlexNet论文
