基础算法(二)

目录

一、高精度

1.1高精度加法:

1.2高精度减法

二、前缀和

前缀和

二维前缀和:

三、差分

---

一、高精度

1.1高精度加法:

#include
#include
using namespace std;


const = int N = 1e6 + 10;

vector add(vector &A,vector &B){
    vector C;
    
    int t = 0; //进位
    for(int i = 0;i < A.size() || i < B.size();i++){
        if(i < A.size()) t+=A[i];
        if(i < B.size()) t+=B[i];
        C.push_back(t%10);
        t /= 10;
    }
    if(t) C.push_back(1);
    return C;
}


int main(){
    String a,b;
    vector A,B;
    
    cin>>a>>b; //a='123456'
    
    for(int i = a.size() -1;i>=0 ;i--) A.push_back(a[i] - '0'); //A=[6,5,4,3,2,1]
    for(int i = b.size() - 1;i>=0;i--) B.push_back(b[i] - '0');
    
    
    auto C = add(A,B);
    
    for(int i= C.size() - 1;i>=0;i--) printf("%d",a[i]);
    
    return 0;    
    
}

1.2高精度减法

#include
#include
using namespace std;

//判断A是否>=B

bool cmp(vector &A,vector &B){
    if(A.size() != B.size() ) return A.szie() > B.size();
    for(int i = A.size() - 1;i >= 0;i-- )
        if(A[i] != B[i])
             return A[i] > B[i];
    
    return true;

}
//C = A - B
vector sub(vector &A,vector &B)
{
    vector C;
    for(int i = 0,t=0;i < A.size();i++){
        t = A[i] - t;
        if(i < B.size()) t -= B[i];
        C.push_back((t+10) % 10);
        if(t < 0) t=1;
        else t= 0;
    }
    
    while(C.size() > 1 && C.back() == 0) C.pop_back(); //去掉前导0
    
    return C;
    
}



int main(){
    String a,b;
    vector A,B;
    
    cin>>a>>b; //a='123456'
    
    for(int i = a.size() -1;i>=0 ;i--) A.push_back(a[i] - '0'); //A=[6,5,4,3,2,1]
    for(int i = b.size() - 1;i>=0;i--) B.push_back(b[i] - '0');
    
    if(cmp(a,b)){
        auto C = sub(A,B);
        
        for(int i= C.size() - 1;i>=0;i--) printf("%d",a[i]);
    }
    else{
        auto C = sub(B,A);
        for(int i= C.size() - 1;i>=0;i--) printf("%d",a[i]);
    }
    
    return 0;    
    
}

二、前缀和

前缀和

定义:Sn=a1+a2+...+an

#include
using namespace std;

const int N = 100010;


int n,m;

int a[N],s[N];

int main()
{
    scanf("%d%d",&n,&m);
    
    for(int i = 1;i <= n;i++) scanf("%d",&a[i]);
    
    for(int i = 1;i <= n;i++) s[i] = s[i-1]+a[i];
    
    
    while(m--){
        int l,r;
        scanf("%d%d",&l,&r);
        printf("%d\n",s[r] - s[l  -1]);
    }
    return 0;
}

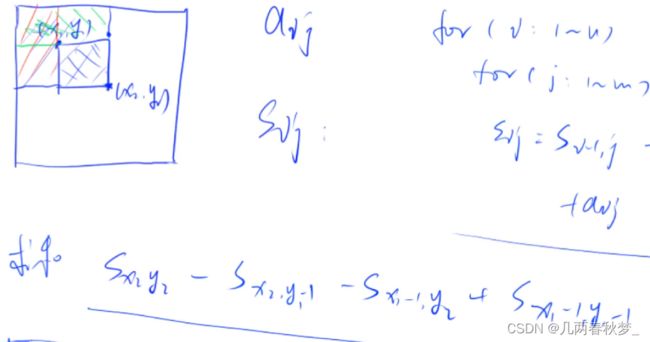
二维前缀和:

基本思路:

 

 模板代码如下:

#include
using namespace std;

const int N = 1010;

int n,m,q;
int a[N][N],s[N][N];

int main(){
    scanf("%d%d%d",&n,&m,&q);
    for(int i = 1;i<= n;i++){
        for(int j = 1;j<= m;j++){
            scanf("%d",&a[i][j])
        }
    }
    for(int i = 1;i<= n;i++){
        for(int j = 1;j<=m;j++){
            s[i][j] = s[i-1][j] + s[i][j-1] - s[i-1][j-1] + a[i][j]; //求前缀和
        }
    }
    
    while(q--){
        int x1,x2,x3,x4;
        scanf("%d%d%d%d",&x1,&x2,&x3,&x4);
        
        printf("%d\n",s[x2][y2] - s[x1-1][y2] - s[x2][y1-1] + s[x1-1][y1-1]);  //算子矩阵
    }
    return 0;
}

三、差分

基本思想: 

 

模板代码如下:

 

#include
using namespace std;

const int N = 100010;

int n,m;
int a[N],b[N];


void insert(int l,int r,int c){
    b[l] += c;
    b[r+1] -= c;

}
int main(){
    scanf("%d%d",&n,&m);
    for(int i = 1;i <= n;i++) scanf("%d",&a[i]);

    for(int i = 1;i <= n;i++) insert(i,i,a[i]); //构造差分数组

    for(int i =1;i<= n;i++){
        printf("%d",b[i]);
    }

    while(m--){
        int l,r,c;
        scanf("%d%d%d",&l,&r,&c);
        insert(l,r,c); //差分操作
    }

    for(int i = 1;i <= n;i++) b[i] += b[i-1];

    for(int i =1;i<= n;i++){
        printf("%d",b[i]);
    }
    return 0;
}