二分法的原理及其应用举例
首先,什么是二分法:
最简单的例子就是类似于二分查找的用法来实现快速查找有序区间内的给定的目标值是否存在,当然,这也可以应用在别的问题中,二分查找是一个时间效率极高的算法,尤其是面对大量的数据时,其查找效率是极高,时间复杂度是log(n)。如果问题是单调的,且求解精确解的难度很高,可以考虑用二分法。
主要思想就是不断的对半折叠,每次查找都能除去一半的数据量,直到最后将所有不符合条件的结果都去除,只剩下一个符合条件的结果。
二分法看似简单,实则在细节上非常容易出错,要注意终止边界,左右区间开闭情况,避免漏掉答案和陷入死循环,在了解了最简单的基本原理之后,我们来由简入繁地以题目来入手理解这个算法,
1.关键的mid的处理
在整个二分法中,对于mid的处理至关重要,如果取值不当,while很容易会死循环,我们来分三点讨论这个问题:
1.1left=mid+1能否写成left=mid?
在实数二分中,确实是left=mid,right=mid,但是在整数二分中存在取整问题,如果取left=mid,会造成原来的left和right值不改变,所以while循环会一直进行下去造成死循环,取left=mid+1则不会。
1.2 不同问题下的mid取值问题
我们要根据不同的问题来识别到底需要左中位数还是右中位数,即对于mid的取值,我们可以向上取整同样的也可以向下取整,要看具体问题的逻辑,我们一般的都使用左中位数,即靠近left的那个数;
1.3谨慎使用(left+right)/2
我们都知道,除法的取整会导致在正负区间左右的中位数计算不一致,虽然一般的情况下,left和right都是正数,在实际计算中,我们可以用mid=left+(right-left)/2或者是mid=(left+right)>>1来替换即可,综合来看,还是(left+right)>>1更优。
下面我们还是来通过例题理解这些知识:
例题一
经典的最大值最小化模型
首先,我们怎样把二分法应用到这个题的求解中,我们知道这个题其实就是想让我们在划分的数组中求出无论怎样划分,其每个分子数组产生的和都有一个确定的最小值,而这个最小值一定介于原数组中的最大的一个元素(最小划分为一个数组)和原数组的所有数组元素的和(最大的一个分组)之间,我们可以在这两个边界之间枚举我们的最大值,采用二分法来寻找最小的那一个数。
我们在代码中来解释细节问题
#include
#include
int n, m;
int l, r, mid, ans;
int a[100010];
//二分答案,枚举出一个最大值,根据分组情况调整最大值,求出最优最大值。
/*
* check 函数
* 作用:
* 根据枚举出的最大值,来分组,根据分出的组数来调整最大值
* 变量:
* x : 枚举出的最大值
* sum : 分组时每组的和
* count : 分出的组数
*/
bool check(int x)
{
int sum=0, count=0;//t2: 组数 t1: 每组的和
for(int i=0; i=m)return true;//objective 2
return false;
}
int main()
{
scanf("%d %d", &n, &m);
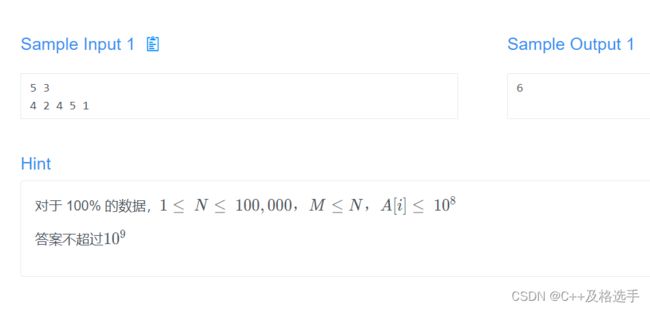
for(int i=0; i 重点其实就在于思路上如何将其与二分法结合在一起考虑问题。
例二
差分数组+二分
我们的注释在题解中见
#include
#include
#include
#include
/*
* line : 原数列
* l, r, d, : 题目要求的 对于每个区间的左端点 右端点 值
* change : 差分数组
* 题解:对采用的订单数进行二分,每次用差分数组优化处理当天需要的教室数并与当天可对外借出的教室数比较检验。-Megumin
*/
int line[1000010], l[1000010], r[1000010], d[1000010], change[1000010];
int n, m;
int check(int x)
{
memset(change, 0, sizeof(change));
for (int i = 1; i <= x; i++)
{
change[l[i]] += d[i];
change[r[i] + 1] -= d[i];
//obj 1用差分数组对前x个操作进行处理
}
//for (int i = 1; i <= n; i++)
// change[i] += (line[i] - line[i - 1]);
//obj 2抹平差分数组 ,此处不需要抹平差分数组,我们只需要默认为line数组全体为零,在将其和我们的change数组结合求出实际上需要的教室数量,再和原来的进行对比看看是否不够来判断非法
int sum = 0;
for (int i = 1; i <= n; i++)
{
sum += change[i];
if (sum>line[i])return false;
//printf("%d ", sum);
}
//obj 3什么情况下是发生了问题?
return true;
}
int main()
{
scanf("%d %d", &n, &m);
for (int i = 1; i <= n; i++)
scanf("%d", &line[i]);
for (int i = 1; i <= m; i++)
scanf("%d %d %d", &d[i], &l[i], &r[i]);
if (check(m))//obj 4什么情况是全都可以成立
{
printf("0");
return 0;
}
int left = 1, right = m, mid;
while (left < right)
{
mid = (left + right) >> 1;
if (check(mid))//obj 5
{
left = mid+1;
}
else
{
right = mid;
}
}
printf("-1\n");
printf("%d", left);
return 0;
}
当然,二分法是一个没有上限的算法,要是展开讲的话肯定是讲不完的,但是二分法的上限是如何将题目转化为二分法进行求解,又将谁二分,上下限如何确定等问题,只需要注意细节,剩下的就要靠日积月累来积累做题思维了。
例三 最小值最大问题
跳石子
我们的重点是在于怎么把这道题和二分法相结合起来,我们发现我们的取值范围在1~l(也就是1~终点)处,我们可以通过二分这段距离,每得到一个中间值,判断这个中间值所代表的的最短跳跃距离是不是合法,如果合法,那么我们的最短跳跃距离还在右边,于是我们把left值改为mid+1,同理,如果我们的mid值不满足,那么我们的最大值的产生一定在左边的区间内,于是将right置为mid-1;
接着我们来思考这个判断过程,我们知道只能移走m块石头,而且我们每移走一块石头,我们的原相邻的两块石头就会变化,这样,我们可以采用类似双指针的做法来判断,具体的看代码理解:
#include
#define maxn 500010
using namespace std;
int a[maxn];
int l, n, m;
inline bool check(int x)
{
int num = 0;
int i = 0, j = 0;
while (i <=n)
{
i++;
if (a[i] - a[j] < x)//移走当前石头的同时,j将会与第i+1个元素相邻所以下一次相比还是j
num++;
else
{
j = i;//接着找下一个
}
if (num > m)
return false;
}
return true;
}
int main()
{
scanf("%d%d%d", &l, &n, &m);
for (int i = 1; i <=n; i++)
{
scanf("%d", &a[i]);
}
a[n + 1] = l;
int left = 1, right = l;
while (left <= right)
{
int mid = (left + right) >> 1;
if (check(mid))
{
left = mid + 1;
}
else
right = mid - 1;
}
printf("%d\n", left-1);
return 0;
} 我们总结二分法在解决实际问题的应用时,本质上我们的二分法是在确定的区间内枚举所有可能的答案,我们寻找的最大最小值,往往就在我们二分判断的结束阶段产生。
金句省身
当你被黑暗敲打的时候,恰好证明你就是光明本身,每一个优秀的人,都会有一段沉默的时光,天赋决定下限,努力决定上限,生活给你压力,你就还它奇迹。
-----致不甘平凡的我们