LeetCode.189(轮转数组)
对于轮转数组这个题,文章一共提供三种思路,对于每种思路均提供其对应代码的时间、空间复杂度。
目录
1. 创建变量来保存最后一个数,并将其余数组向前挪动一位 :
1.1 原理解析:
1.2 代码实现:
2.创建一个数组,用于存放需要旋转的元素,并放到相应位置:
2.1 原理解析:
2.2 代码实现:
3. 先左部分右旋,再右部分右旋,最后整体逆序(三段逆序法):
3.1 原理解析:
3.2 代码实现:
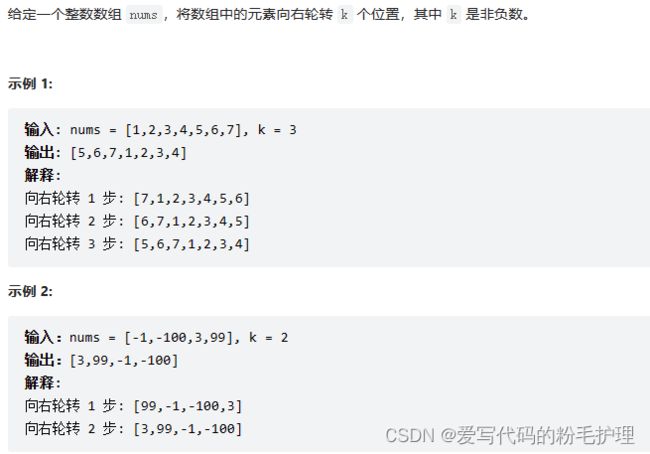
题目要求如图所示:
1. 创建变量来保存最后一个数,并将其余数组向前挪动一位 :
(注:第一种思路虽然可以解决问题,但是代码的时间复杂度为![]() ,空间复杂度为
,空间复杂度为![]() ,时间复杂度不符合LeetCode的提交标准,所以,第一种思路仅供参考与扩展。)
,时间复杂度不符合LeetCode的提交标准,所以,第一种思路仅供参考与扩展。)
1.1 原理解析:
假设一个数组为:
nums[7] = {1,2,3,4,5,6,7};为了方便表示,用下图来代表数组及数组中的元素:
第一步:先将数组种最后一位元素,即:7,用一个临时变量保存。
第二步:将其他剩余元素全部向右移动一位。
第三步: 把临时变量保存的7,放到数组的首元素的位置。
至此,完成一次交换。
1.2 代码实现:
用代码表示上述过程,即:
#include
#include
void rotata(int* nums,int numsize)
{
assert(nums);
int tmp = nums[numsize - 1];//用临时变量保存数组最后一个元素
int i = 0;
for (i = 6 ; i > 0; i--)
{
nums[i] = nums[i - 1];//将其余元素向右移动一位
}
nums[0] = tmp;//将临时变量保存的元素放在数组首个元素的位置
}
int main()
{
int nums[7] = { 1,2,3,4,5,6,7 };
int sz = sizeof(nums) / sizeof(nums[0]);
rotata(nums, sz );
return 0;
} 打印结果如下:
上面的代码,只能实现右移一位。对于移动多个元素,可以将上面移动一个元素的过程用循环来进行。例如,用变量![]() 来代表旋转的次数,代码为:
来代表旋转的次数,代码为:
#include
#include
void rotata(int* nums,int numsize,int k)
{
k = k % numsize + 1;//防止k过大,使k的范围在0-7
assert(nums);
int j = 0;
for (j = 0; j < k; j++)
{
int tmp = nums[numsize - 1];//用临时变量保存数组最后一个元素
int i = 0;
for (i = 6; i > 0; i--) //0 1 2 3 4 5 6
// 1 2 3 4 5 6
{
nums[i] = nums[i - 1];//将其余元素向右移动一位
}
nums[0] = tmp;//将临时变量保存的元素放在数组首个元素的位置
}
}
int main()
{
int nums[7] = { 1,2,3,4,5,6,7 };
int sz = sizeof(nums) / sizeof(nums[0]);
int k = 0;
scanf("%d", &k);
rotata(nums, sz,k );
int i = 0;
return 0;
} 因为数组每旋转7次,数组中的元素就回到不旋转的位置,所以,即使在输入旋转次数为77次时,得到的效果也和旋转一次一样
旋转一次效果:
旋转两次效果:
旋转77次:
但是,当![]() 的值过大时,因为每右旋7次就是一个循环,所以,为了减少编译器的工作量,用
的值过大时,因为每右旋7次就是一个循环,所以,为了减少编译器的工作量,用![]() %
%![]()
![]() ,让
,让![]() 的取值范围保持在
的取值范围保持在![]() 这个区间(闭区间)
这个区间(闭区间)
2.创建一个数组,用于存放需要旋转的元素,并放到相应位置:
方法二的时间复杂度为![]() ,空间复杂度为
,空间复杂度为![]()
2.1 原理解析:
依旧使用上面的图来解释思路:
右旋一次:
右旋两次:
对于上面的两种情况,不难发现,其实所谓的右旋,可理解为将需要进行右旋的元素看成一个整体,让后放到其余元素的前面,例如旋转两次时:
第一步:将元素![]() 看作一个整体,其余元素看成一个整体。
看作一个整体,其余元素看成一个整体。
第二步:作为整体的![]() 放到剩余元素的前面进行整合:
放到剩余元素的前面进行整合:
2.2 代码实现:
有了解决问题的思路后,下面给出具体实现的代码:
void rotate(int* nums, int numsSize, int k){
int n = numsSize;
int* tmp = (int*)malloc(sizeof(int)*(n));
k = k%n;
memcpy(tmp,nums+n-k,sizeof(int)*(k));
memcpy(tmp+k,nums,sizeof(int)*(n-k));
memcpy(nums,tmp,sizeof(int)*(n));
free(tmp);
}整体代码的逻辑为: n是数组中元素的个数,k是执行右旋的次数。
1.先用malloc开辟一块空间
2.用![]() %
%![]() 来限制
来限制![]() 的取值范围。
的取值范围。
3.先利用memcpy函数将nums数组种起始地址![]() ,数量为
,数量为![]() 的元素拷贝到tmp这个临时空间种。
的元素拷贝到tmp这个临时空间种。
4.再利用memcpy函数将nums剩余的元素拷贝到tmp中。
此时,tmp已经存储了旋转后的数组。
5.将tmp中的元素赋值到nums中。
执行结果如下:
从结果中可以看到,方法二是用空间来换取速度的方法。
3. 先左部分右旋,再右部分右旋,最后整体逆序(三段逆序法):
最优解法,时间复杂度为![]() ,空间复杂度因为只创建了一个额外的临时变量,为
,空间复杂度因为只创建了一个额外的临时变量,为![]()
3.1 原理解析:
对于三段逆序法,同样使用图片来解释:
假设:数组名为![]() ,数组中的元素个数为
,数组中的元素个数为![]() ,按照LeetCode中7个元素。需要旋转的位数为
,按照LeetCode中7个元素。需要旋转的位数为![]() 。下面的代码就拿
。下面的代码就拿![]() 来解释。
来解释。
第一步:先将左部分元素整体逆序,即:把下标从0到![]() (即数组中第一个到第四个元素逆序)的元素逆序:
(即数组中第一个到第四个元素逆序)的元素逆序:
第二步:将右半部分元素整体逆序,即:把下标为![]() 到
到![]() (即数组中第五个到第七个元素逆序):
(即数组中第五个到第七个元素逆序):
第三步:整体逆序:即:对下标从0到![]() 的元素逆序:
的元素逆序:
通过LeetCode网站给出的样例发现,整体逆序后结果与样例相同:
3.2 代码实现:
在上面的解释中,既然每一步都需要逆序,所以,为了方便并且减少代码量,可以提前封装一个交换函数或者直接使用交换函数,这里给出提前封装交换函数的代码:
其中:变量![]() 对应数组
对应数组![]() ,变量
,变量![]() 对应交换的起始位置,变量
对应交换的起始位置,变量![]() 对于交换的结束位置
对于交换的结束位置
void reserve( int*a,int left,int right)
{
while(left < right)
{
int tmp = a[left];
a[left] = a[right];
a[right] = tmp;
left++;
right--;
}
}再交换后,根据上面对原理的解释,对逆序函数进行三次调用并传递相应的参数即可:
void rotate(int* nums, int numsSize, int k){
int n = numsSize;
k = k%n;
reserve(nums,0,n-k-1);
reserve(nums,n-k,n-1);
reserve(nums,0,n-1);
}整体函数如下:
void reserve( int*a,int left,int right)
{
while(left < right)
{
int tmp = a[left];
a[left] = a[right];
a[right] = tmp;
left++;
right--;
}
}
void rotate(int* nums, int numsSize, int k){
int n = numsSize;
k = k%n;
reserve(nums,0,n-k-1);
reserve(nums,n-k,n-1);
reserve(nums,0,n-1);
}运行结果如下: