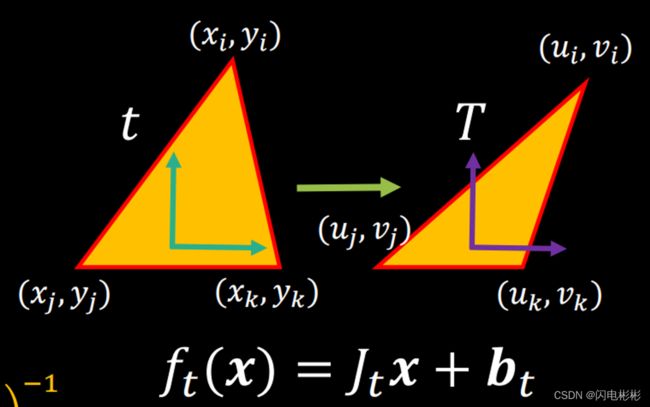网格参数化方法
参数化的作用
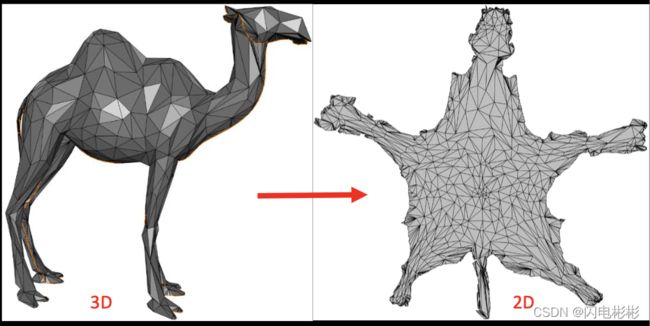
简单说就是把三维三角网格在二维上展开。由于曲率的存在,肯定存在变形。参数化要研究的问题就是如何让变形最小。
参数化后的二维平面可以存储很多信息,比如法向,纹理等。
可应用在纹理贴图,二维三维联动等。
tutte’s embedding 算法
该算法可以处理与圆盘同胚非闭合的三角网格面,他能保证3D与2D是一一映射的。
算法过程
- 先把边界点按照顺序均匀地放置在圆边界上。
- 对于内部的点,vi 是周围顶点的线性组合。
v i = ∑ j ∈ Ω ( i ) d i v j , d i 是 顶 点 v i 的 度 。 v_i = \displaystyle \sum_{j \in \Omega(i)} {d_iv_j}, d_i是顶点v_i的度。 vi=j∈Ω(i)∑divj,di是顶点vi的度。
n个未知顶点,n个方程刚好解出来。
算法实现
github: https://github.com/LightningBilly/ACMAlgorithms/tree/master/%E5%9B%BE%E5%BD%A2%E5%AD%A6%E7%AE%97%E6%B3%95/%E4%B8%89%E8%A7%92%E7%BD%91%E6%A0%BC%E7%AE%97%E6%B3%95/MeshWork/src/hw4
#include "hw4.h"
#include 算法效果
最小二乘保角参数化(LSCM)
重心坐标
已知三角形的三点坐标,以及定义在顶点上的函数f,那么三角形内一点f值可以通过插值的方式得到。

f ( x ) = α f i + β f j + γ f k f(x)=\alpha f_i +\beta f_j + \gamma f_k f(x)=αfi+βfj+γfk
其中
α = S i S i + S j + S k , S i 是 x i 的 对 边 与 x 组 成 的 三 角 形 的 面 积 , S j , S k , β , γ 同 理 \alpha =\frac {S_i}{S_i+S_j+S_k}, S_i是x_i的对边与x组成的三角形的面积,S_j, S_k, \beta, \gamma 同理 α=Si+Sj+SkSi,Si是xi的对边与x组成的三角形的面积,Sj,Sk,β,γ同理
线性分片性质
从上式可看出f(x)是一个分片线性函数。
那么, f(x)就可以由一个Jacobi矩阵乘上x再加一个列向量得到。
f ( x ) = J x + b , J 是 J a c o b i 矩 阵 f(x)=Jx+b,J是Jacobi矩阵 f(x)=Jx+b,J是Jacobi矩阵
J 就 是 先 对 f ( x ) 求 偏 导 , 再 对 x 求 偏 导 J就是先对f(x)求偏导,再对x求偏导 J就是先对f(x)求偏导,再对x求偏导
形 式 如 下 J = [ ∂ u ∂ x ∂ v ∂ x . . . ∂ u ∂ y ∂ v ∂ y . . . ∂ u ∂ z ∂ v ∂ z . . . ] 形式如下J=\begin {bmatrix} \frac {∂u}{∂x}&\frac {∂v}{∂x}&... \\ \frac {∂u}{∂y}&\frac {∂v}{∂y}&... \\ \frac {∂u}{∂z}&\frac {∂v}{∂z}&... \end{bmatrix} 形式如下J=⎣⎡∂x∂u∂y∂u∂z∂u∂x∂v∂y∂v∂z∂v.........⎦⎤
u, v 是f函数值的分量,如果有多个分量J就有多列。
梯度
上面的J矩阵,在三角形中表现为梯度。
梯度就是将f函数对x进行求导。
∇ x f ( x ) = f i ∇ x α + f j ∇ x β + f k ∇ γ \nabla_xf(x)=f_i\nabla_x\alpha+f_j\nabla_x\beta+f_k\nabla\gamma ∇xf(x)=fi∇xα+fj∇xβ+fk∇γ
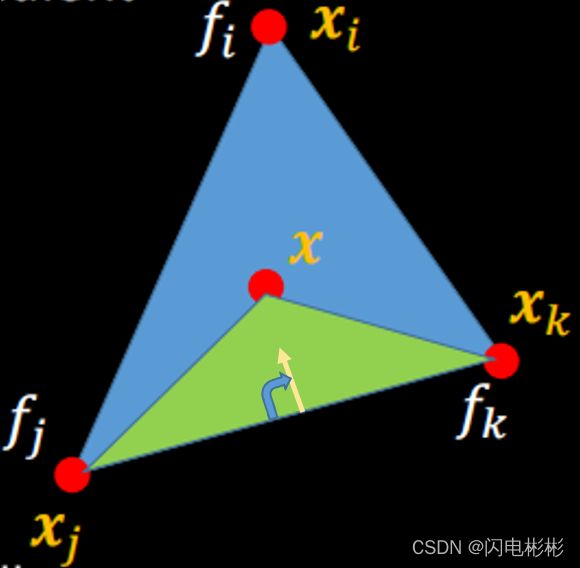
面积Si要怎么求。
利用底乘以高。
底就是向量xk-xj的模,黄色向量是与xk-xj垂直的单位向量,高就是x-xj在黄向量的投影,可以用点积得到。
黄色向量可以使用xk-xj转90度取单位向量得到。
α = A i A T = ( x − x j ) ⋅ ( x k − x j ) ⊥ ∣ ∣ x k − x j ∣ ∣ 2 ∣ ∣ x k − x j ∣ ∣ 2 2 A T = ( x − x j ) ⋅ ( x k − x j ) ⊥ 2 A T \alpha=\frac {A_i} {A^T}=\frac {(x-x_j)\cdot \frac {(x_k-x_j)^\perp }{||x_k-x_j||_2}||x_k-x_j||_2}{2A^T}=\frac {(x-x_j)\cdot {(x_k-x_j)^\perp }}{2A^T} α=ATAi=2AT(x−xj)⋅∣∣xk−xj∣∣2(xk−xj)⊥∣∣xk−xj∣∣2=2AT(x−xj)⋅(xk−xj)⊥
只 有 前 面 和 x 变 量 有 关 , ∇ x α = ( x k − x j ) ⊥ 2 A T 只有前面和x变量有关,\nabla_x\alpha=\frac {(x_k-x_j)^\perp}{2A^T} 只有前面和x变量有关,∇xα=2AT(xk−xj)⊥
∇ x f ( x ) = f i ( x k − x j ) ⊥ 2 A T + f j ( x i − x k ) ⊥ 2 A T + f k ( x j − x i ) ⊥ 2 A T \nabla_xf(x)=f_i\frac {(x_k-x_j)^\perp}{2A^T}+f_j\frac {(x_i-x_k)^\perp}{2A^T}+f_k\frac {(x_j-x_i)^\perp}{2A^T} ∇xf(x)=fi2AT(xk−xj)⊥+fj2AT(xi−xk)⊥+fk2AT(xj−xi)⊥
这里可以看出一个三角的面的梯度是一个常数。
保角参数化基本思想
参数化以后是一个二维平面,保角的意思是希望二维平面的三角形与三维对应的三角形的角尽量相等。
那我们不妨先将三维的三角形摊平到2D上,然后进行变换。
相当于在2D三角形的顶点上定义了一个函数f, 经过函数f处理后就是参数化坐标,f(x) = [u, v]。
这里的x是一个二维坐标。
根据线性分片性质f(x) = Jx+b。
J = [ ∂ u ∂ x ∂ u ∂ y ∂ v ∂ x ∂ v ∂ y ] J=\begin {bmatrix} \frac {∂u}{∂x}&\frac{∂u}{∂y}\\ \frac {∂v}{∂x}&\frac{∂v}{∂y} \end {bmatrix} J=[∂x∂u∂x∂v∂y∂u∂y∂v]
如果希望保角,那就要使J矩阵尽量是一个旋转矩阵。
旋 转 矩 阵 是 这 样 , [ c o s ∂ − s i n ∂ s i n ∂ c o s ∂ ] 旋转矩阵是这样,\begin {bmatrix} cos∂&-sin∂\\sin∂&cos∂ \end {bmatrix} 旋转矩阵是这样,[cos∂sin∂−sin∂cos∂]
可以看出主对角是相等,副对角为相反数。
∂ u ∂ x = ∂ v ∂ y , ∂ u ∂ y = − ∂ v ∂ x 需 要 使 这 2 个 式 子 成 立 , 完 全 相 等 是 不 可 能 的 , 只 能 是 尽 量 接 近 \frac {∂u}{∂x}=\frac{∂v}{∂y} ,\frac{∂u}{∂y}=- \frac {∂v}{∂x} 需要使这2个式子成立,完全相等是不可能的,只能是尽量接近 ∂x∂u=∂y∂v,∂y∂u=−∂x∂v需要使这2个式子成立,完全相等是不可能的,只能是尽量接近
可以建立能量函数 Q = ∑ Q t = ∑ S t [ ( ∂ u ∂ x − ∂ v ∂ y ) 2 + ( ∂ u ∂ y + ∂ v ∂ x ) 2 ] Q=\sum Q_t = \sum S_t \left [ \left( \frac {∂u}{∂x}-\frac{∂v}{∂y} \right )^2+\left(\frac{∂u}{∂y}+ \frac {∂v}{∂x} \right)^2\right ] Q=∑Qt=∑St[(∂x∂u−∂y∂v)2+(∂y∂u+∂x∂v)2]
一个t代表一个三角形。
优化这个函数使得Q最小就可以保角了。
下面求解一下J矩阵。
J = ∇ x f ( x ) = f i ( x k − x j ) ⊥ 2 A T + f j ( x i − x k ) ⊥ 2 A T + f k ( x j − x i ) ⊥ 2 A T J=\nabla_xf(x)=f_i\frac {(x_k-x_j)^\perp}{2A^T}+f_j\frac {(x_i-x_k)^\perp}{2A^T}+f_k\frac {(x_j-x_i)^\perp}{2A^T} J=∇xf(x)=fi2AT(xk−xj)⊥+fj2AT(xi−xk)⊥+fk2AT(xj−xi)⊥
先解决旋转问题。
旋 转 90 度 矩 阵 : r o t a t e 90 = [ c o s 9 0 0 − s i n 9 0 0 s i n 9 0 0 c o s 9 0 0 ] = [ 0 − 1 1 0 ] 旋转90度矩阵:rotate90 = \begin {bmatrix} cos90^0&-sin90^0 \\ sin90^0&cos90^0 \end {bmatrix} = \begin {bmatrix} 0&-1 \\1 &0 \end {bmatrix} 旋转90度矩阵:rotate90=[cos900sin900−sin900cos900]=[01−10]
( x k − x j ) ⊥ = [ c o s 9 0 0 − s i n 9 0 0 s i n 9 0 0 c o s 9 0 0 ] [ x k − x j y k − y j ] = [ − ( y k − y j ) x k − x j ] (x_k-x_j)^\perp = \begin {bmatrix} cos90^0&-sin90^0 \\ sin90^0&cos90^0 \end {bmatrix} \begin {bmatrix} x_k-x_j \\ y_k-y_j \end {bmatrix} = \begin {bmatrix} -(y_k-y_j) \\ x_k-x_j \end {bmatrix} (xk−xj)⊥=[cos900sin900−sin900cos900][xk−xjyk−yj]=[−(yk−yj)xk−xj]
其他同理。
J矩阵坐标表示:
J = 1 2 A [ − ( y k − y j ) − ( y i − y k ) − ( y j − y i ) x k − x j x i − x k x j − y i ] [ f i f j f k ] J=\frac {1}{2A}\begin {bmatrix} -(y_k-y_j)& -(y_i-y_k) & - (y_j-y_i) \\ x_k-x_j&x_i-x_k&x_j-y_i \end {bmatrix}\begin {bmatrix} f_i\\f_j \\f_k \end {bmatrix} J=2A1[−(yk−yj)xk−xj−(yi−yk)xi−xk−(yj−yi)xj−yi]⎣⎡fifjfk⎦⎤
= 1 2 A [ − ( y k − y j ) − ( y i − y k ) − ( y j − y i ) x k − x j x i − x k x j − y i ] [ u i v i u j v j u k v k ] = [ ∂ u ∂ x ∂ u ∂ y ∂ v ∂ x ∂ v ∂ y ] =\frac {1}{2A}\begin {bmatrix} -(y_k-y_j)& -(y_i-y_k) & - (y_j-y_i) \\ x_k-x_j&x_i-x_k&x_j-y_i \end {bmatrix}\begin {bmatrix} u_i&v_i\\u_j&v_j \\u_k&v_k \end {bmatrix}=\begin {bmatrix} \frac {∂u}{∂x}&\frac{∂u}{∂y}\\ \frac {∂v}{∂x}&\frac{∂v}{∂y} \end {bmatrix} =2A1[−(yk−yj)xk−xj−(yi−yk)xi−xk−(yj−yi)xj−yi]⎣⎡uiujukvivjvk⎦⎤=[∂x∂u∂x∂v∂y∂u∂y∂v]
= 1 2 A [ k 1 k 2 k 3 k 4 k 5 k 6 ] [ u i v i u j v j u k v k ] =\frac {1}{2A}\begin {bmatrix} k_1& k_2 & k_3 \\ k_4&k_5&k_6 \end {bmatrix}\begin {bmatrix} u_i&v_i\\u_j&v_j \\u_k&v_k \end {bmatrix} =2A1[k1k4k2k5k3k6]⎣⎡uiujukvivjvk⎦⎤
= [ k 1 k 2 k 3 k 4 k 5 k 6 ] [ u i v i u j v j u k v k ] =\begin {bmatrix} k_1& k_2 & k_3 \\ k_4&k_5&k_6 \end {bmatrix}\begin {bmatrix} u_i&v_i\\u_j&v_j \\u_k&v_k \end {bmatrix} =[k1k4k2k5k3k6]⎣⎡uiujukvivjvk⎦⎤
= [ k 1 ∗ u i + k 2 ∗ u j + k 3 ∗ u k k 1 ∗ v i + k 2 ∗ v j + k 3 ∗ v k k 4 ∗ u i + k 5 ∗ u j + k 6 ∗ u k k 4 ∗ v i + k 5 ∗ v j + k 6 ∗ v k ] =\begin {bmatrix} k_1*u_i+ k_2*u_j +k_3*u_k & k_1*v_i+ k_2*v_j +k_3*v_k \\ k_4*u_i+ k_5*u_j +k_6*u_k & k_4*v_i+ k_5*v_j +k_6*v_k \end {bmatrix} =[k1∗ui+k2∗uj+k3∗ukk4∗ui+k5∗uj+k6∗ukk1∗vi+k2∗vj+k3∗vkk4∗vi+k5∗vj+k6∗vk]
k n 是 已 知 量 , 代 入 Q 式 子 中 , Q 是 关 于 u , v 的 二 次 多 项 , 只 要 求 驻 点 就 可 以 得 到 最 小 值 。 求 导 后 可 以 通 过 最 小 二 乘 解 决 。 k_n 是已知量,代入Q式子中,Q是关于u,v的二次多项,\\ 只要求驻点就可以得到最小值。求导后可以通过最小二乘解决。 kn是已知量,代入Q式子中,Q是关于u,v的二次多项,只要求驻点就可以得到最小值。求导后可以通过最小二乘解决。
代码实现
实际实现时是用了复分析的方法,具体可以参考以下文章:
https://blog.csdn.net/why18767183086/article/details/107870019
https://blog.csdn.net/weixin_49732532/article/details/107822729
https://www.zhihu.com/people/allan-35-49/posts
https://github.com/icemiliang/lscm
效果
ABF
Angle-Based Flattening(ABF) 是计算出参数化后各三角形的角度,使得角度与原来的角度相差最小。然后再利用角度来恢复出三角形的参数化方法。
基于这个思想给出能量方程以及约束条件:
E A B F = ∑ t ∑ i = 1 3 ω i t ( α i t − β i t ) 2 E_{ABF}=\displaystyle \sum_t\displaystyle \sum_{i=1}^{3}\omega_i^t(\alpha_i^t-\beta_i^t)^2 EABF=t∑i=1∑3ωit(αit−βit)2
β i t 是 优 化 的 目 标 角 度 , α i t 是 变 量 ω i t = ( β i t ) − 2 \beta_i^t是优化的目标角度,\alpha_i^t是变量 \\ \omega_i^t=(\beta_i^t)^{-2} βit是优化的目标角度,αit是变量ωit=(βit)−2
β i t 需 要 归 一 化 , β i t = { β ~ i t ⋅ 2 π ∑ i β i t , 内 部 结 点 β ~ i t , 边 界 结 点 \beta_i^t 需要归一化, \;\beta_i^t= \left\{\begin{array}{l}\frac {\widetilde{\beta}_i^t\cdot 2\pi}{\sum_i\beta_i^t}, \;内部结点\\ \widetilde{\beta}_i^t, \; 边界结点\end{array}\right. βit需要归一化,βit={∑iβitβ it⋅2π,内部结点β it,边界结点
约束条件如下:
所有的角都要为正
α i t > 0 \alpha_i^t >0 αit>0
三角形内角和为180度
α 1 t + α 2 t + α 3 t = π \alpha_1^t+\alpha_2^t+\alpha_3^t=\pi α1t+α2t+α3t=π
一个项点所有的所有三角形,以该点所形成的角和为360度
∑ t ∈ Ω ( v ) α k t = 2 π \displaystyle \sum_{t \in \Omega(v)}{\alpha_k^t}=2\pi t∈Ω(v)∑αkt=2π
限制边长关系使得最后三角形可以合上
∏ t ∈ Ω ( v ) sin α k ⊕ 1 t = ∏ t ∈ Ω ( v ) sin α k ⊝ 1 t \prod_{t\in\Omega(v)}\sin\alpha_{k\oplus1}^{t}=\prod_{t\in\Omega(v)}\sin\alpha_{k\circleddash1}^t ∏t∈Ω(v)sinαk⊕1t=∏t∈Ω(v)sinαk⊝1t
LABF
上述方法中
∏ t ∈ Ω ( v ) sin α k ⊕ 1 t = ∏ t ∈ Ω ( v ) sin α k ⊝ 1 t \prod_{t\in\Omega(v)}\sin\alpha_{k\oplus1}^{t}=\prod_{t\in\Omega(v)}\sin\alpha_{k\circleddash1}^t ∏t∈Ω(v)sinαk⊕1t=∏t∈Ω(v)sinαk⊝1t
这个条件是一个非线性约束,这使得求解时非常麻烦。
LABF的思想是先把这个条件变成一个线性约束条件,再来求解。
设 α i t = β i t + e i t 设\alpha_i^t=\beta_i^t+e_i^t 设αit=βit+eit
先对原式取log
l o g ( ∏ t ∈ Ω ( v ) sin α k ⊕ 1 t ) = l o g ( ∏ t ∈ Ω ( v ) sin α k ⊝ 1 t ) log\left ( \prod_{t\in\Omega(v)}\sin\alpha_{k\oplus1}^t\right)=log\left ( \prod_{t\in\Omega(v)}\sin\alpha_{k\circleddash1}^t\right) log⎝⎛t∈Ω(v)∏sinαk⊕1t⎠⎞=log⎝⎛t∈Ω(v)∏sinαk⊝1t⎠⎞
∑ t ∈ Ω ( v ) log ( sin α k ⊕ 1 t ) = ∑ t ∈ Ω ( v ) log ( sin α k ⊝ 1 t ) \displaystyle \sum_{t\in\Omega(v)}\log(\sin\alpha_{k\oplus1}^t)=\displaystyle\sum_{t\in\Omega(v)}\log(\sin\alpha_{k\circleddash1}^t) t∈Ω(v)∑log(sinαk⊕1t)=t∈Ω(v)∑log(sinαk⊝1t)
利用泰勒展开得到
log ( sin α k ⊕ 1 t ) = log ( sin β k ⊕ 1 t + e k ⊕ 1 t ) \log(\sin \alpha_{k\oplus1}^t)=\log (\sin \beta_{k\oplus1}^t+e_{k\oplus1}^t) log(sinαk⊕1t)=log(sinβk⊕1t+ek⊕1t)
= log ( sin β k ⊕ 1 t ) + e k ⊕ 1 t cot β k ⊕ 1 t + . . . =\log(\sin \beta_{k\oplus1}^t)+e_{k\oplus1}^t\cot\beta_{k\oplus1}^t+... =log(sinβk⊕1t)+ek⊕1tcotβk⊕1t+...
那么原来的E可以转化成 e的方程
E A B F = ∑ t ∑ i = 1 3 ω i t ( e i t ) 2 E_{ABF}=\displaystyle \sum_t\displaystyle \sum_{i=1}^{3}\omega_i^t(e_i^t)^2 EABF=t∑i=1∑3ωit(eit)2
利用拉格朗日乘子法可以得到
A e = b Ae=b Ae=b
[ D A T A 0 ] [ e λ ] = [ 0 b ] \begin {bmatrix} D&A^T\\ A&0 \end {bmatrix}\begin {bmatrix} e\\ \lambda \end {bmatrix} = \begin {bmatrix} 0\\ b \end {bmatrix} [DAAT0][eλ]=[0b]
解得:
e = D − 1 A T ( A D − 1 A T ) − 1 b e = D^{-1}A^T(AD^{-1}A^T)^{-1}b e=D−1AT(AD−1AT)−1b
基于角度还原出参数化结果
贪心算法
先放一个种子三角形,对3条边进行深度优先遍历摆放三角形。
该方法不足之处是,由于浮点有计算误差,摆放过程中误差会越来越大,最后导致有一些三角形的边无法合上。
基于优化的算法

根据2边之比等于对角的sin之比可以得到
∣ ∣ P 1 P 3 → ∣ ∣ ∣ ∣ P 1 P 2 → ∣ ∣ = sin α 2 sin α 3 \frac {||\overrightarrow{P_1P_3}||}{||\overrightarrow{P_1P_2}||}=\frac {\sin \alpha_2}{\sin\alpha_3} ∣∣P1P2∣∣∣∣P1P3∣∣=sinα3sinα2
向 量 P 1 P 3 → 可 以 看 成 是 P 1 P 2 → 逆 时 针 旋 转 再 乘 以 一 个 比 例 得 到 向量\overrightarrow{P_1P_3} 可以看成是 \overrightarrow{P_1P_2}逆时针旋转再乘以一个比例得到 向量P1P3可以看成是P1P2逆时针旋转再乘以一个比例得到
P 1 P 3 → = sin α 2 sin α 3 [ cos α 1 − sin α 1 sin α 1 cos α 1 ] P 1 P 2 → \overrightarrow{P_1P_3} = \frac {\sin \alpha_2}{\sin\alpha_3} \begin{bmatrix} \cos\alpha_1&-\sin\alpha_1 \\ \sin\alpha_1&\cos\alpha_1 \end{bmatrix}\overrightarrow{P_1P_2} P1P3=sinα3sinα2[cosα1sinα1−sinα1cosα1]P1P2
所 以 对 于 一 个 正 常 的 三 角 形 P 1 P 3 → = sin α 2 sin α 3 [ cos α 1 − sin α 1 sin α 1 cos α 1 ] ( P 2 − P 1 ) − ( P 3 − P 1 ) = 0 所以对于一个正常的三角形\overrightarrow{P_1P_3} = \frac {\sin \alpha_2}{\sin\alpha_3} \begin{bmatrix} \cos\alpha_1&-\sin\alpha_1 \\ \sin\alpha_1&\cos\alpha_1 \end{bmatrix}(P_2-P_1) - (P_3-P_1)=0 所以对于一个正常的三角形P1P3=sinα3sinα2[cosα1sinα1−sinα1cosα1](P2−P1)−(P3−P1)=0
实际中做不到等于0,只能是使其越接近越好。
可以针对所有三角形列出一个能量方程
E = ∑ t ∣ ∣ sin α 2 t sin α 3 t [ cos α 1 t − sin α 1 t sin α 1 t cos α 1 t ] ( P 2 t − P 1 t ) − ( P 3 t − P 1 t ) ∣ ∣ 2 E=\displaystyle \sum_t{|| \frac {\sin \alpha_2^t}{\sin\alpha_3^t} \begin{bmatrix} \cos\alpha_1^t&-\sin\alpha_1^t \\ \sin\alpha_1^t&\cos\alpha_1^t \end{bmatrix}(P_2^t-P_1^t) - (P_3^t-P_1^t)||^2} E=t∑∣∣sinα3tsinα2t[cosα1tsinα1t−sinα1tcosα1t](P2t−P1t)−(P3t−P1t)∣∣2
优化上述方程即可得到参数化结果。
as-rigid-as-possible (ASAP)
尽量做保边长的变换。就是为每个三个角形找到一个单纯的旋转矩阵,lscm是找到一个旋转+缩放。asap只要旋转,不要缩放。
能量方程:
E ( u , L ) = ∑ t A t ∣ ∣ J t − L t ∣ ∣ F 2 E(u,L) = \displaystyle \sum_t{A_t}||J_t-L_t||_F^2 E(u,L)=t∑At∣∣Jt−Lt∣∣F2
L t 是 三 角 形 的 目 标 旋 转 矩 阵 L_t是三角形的目标旋转矩阵 Lt是三角形的目标旋转矩阵
J t 是 三 角 形 的 实 际 的 变 换 矩 阵 J_t是三角形的实际的变换矩阵 Jt是三角形的实际的变换矩阵
当 给 定 J t 时 , 由 于 每 个 三 角 形 是 独 立 的 , 所 以 L t 可 分 开 求 解 当给定J_t时,由于每个三角形是独立的,所以L_t可分开求解 当给定Jt时,由于每个三角形是独立的,所以Lt可分开求解
对 J t 做 S V D 分 解 , J t = U ∑ V T , ∑ = [ σ 1 0 0 σ 2 ] , L t 最 优 值 为 U V T 对J_t做SVD分解,J_t=U\sum V^T, \sum=\begin{bmatrix} \sigma_1&0 \\ 0&\sigma_2 \end {bmatrix}, L_t最优值为UV^T 对Jt做SVD分解,Jt=U∑VT,∑=[σ100σ2],Lt最优值为UVT
当 L t 确 定 时 , E ( u , L ) 是 一 个 二 次 多 项 式 , 可 通 过 求 导 , 利 用 最 小 二 乘 求 解 。 当L_t确定时,E(u, L) 是一个二次多项式,可通过求导,利用最小二乘求解。 当Lt确定时,E(u,L)是一个二次多项式,可通过求导,利用最小二乘求解。
具体求解时E可以表示成边和点的多项式。可以参考https://blog.csdn.net/why18767183086/article/details/108034725
代码实现
// arap_parameterizations
#include