24考研数据结构-队列1

3.2队列（Queue）

3.2.1队列的基本概念

1. 定义：队列（Queue）简称队，是一种操作受限的线性表，只允许在表的一端进行插入，而在表的另一端进行删除。
2. 特点

• 队列是操作受限的线性表，只允许在一端进行插入 (入队)，另一端进行删除 (出队)
• 操作特性：先进先出 FIFO
• 队头：允许删除的一端
• 队尾：允许插入的一端
• 空队列：不含任何元素的空表

3. 队列的基本操作

• “创建&销毁”

InitQueue(&Q): 初始化队列，构造一个空列表Q
DestroyQueue(&Q): 销毁队列，并释放队列Q所占用的内存空间

• “增&删”

EnQueue(&Q, x): 入队，若队列Q未满，将x加入，使之成为新的队尾
DeQueue(&Q, &x): 出队，若队列Q非空，删除队头元素，并用x返回

• “查&其他”

GetHead(Q,&x): 读队头元素，若队列Q非空，则将队头元素赋值给x
QueueEmpty(Q): 判队列空，若队列Q为空，则返回

3.2.2队列的顺序存储结构

队头指针：指向队头元素
队尾指针：指向队尾元素的下一个位置

3.2.2.1 队列存储的基本操作

//队列的顺序存储类型
# define MaxSize 10;     //定义队列中元素的最大个数
typedef struct{
    ElemType data[MaxSize];   //用静态数组存放队列元素
                              //连续的存储空间，大小为
                              //MaxSize*sizeof(ElemType)
    int front, rear;          //队头指针和队尾指针
}SqQueue;

//初始化队列
void InitQueue(SqQueue &Q){
    //初始化时，队头、队尾指针指向0
    Q.rear = Q.front = 0;
}

void test{
    SqQueue Q;                //声明一个队列
    InitQueue(Q);
    //...
}

// 判空
bool QueueEmpty(SqQueue 0){
    if(Q.rear == Q.front)    //判空条件
        return true;
    else 
        return false;
}

1. 用静态数组存放队列元素，连续的存储空间，大小为MaxSize*sizeof(ElemType)
2. int front, rear; //队头指针和队尾指针
3. if(Q.rear == Q.front) //判空条件

用int类型表示数据在队伍的相对位置，相当于用数组的下标来表示元素的位置
front指向队头元素，rear指向下一个空缺的位置

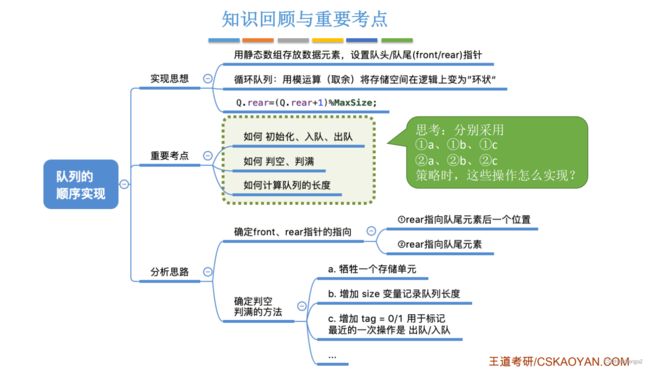
3.2.2.2 循环队列$基本操作和判空方式$

定义：将循环队列臆造为一个环状的空间，即把存储队列元素的表从逻辑上视为一个环，称为循环队列。
基本操作：

a%b == a除以b的余数

初始：Q.front = Q.rear = 0;

队首指针进1：Q.front = (Q.front + 1) % MaxSize

队尾指针进1：Q.rear = (Q.rear + 1) % MaxSize —— 队尾指针后移，当移到最后一个后，下次移动会到第一个位置

队列长度：(Q.rear + MaxSize - Q.front) % MaxSize

$重点是这个循环队列的判断空的方式，以下是几种方式，这些方式都是为了与$
$队列的判空条件Q.front=Q.rear；区分开$

方案一: 牺牲一个单元来区分队空和队满
队尾指针的再下一个位置就是队头，即 (Q.rear+1)%MaxSize == Q.front

循环队列——入队：只能从队尾插入（判满使用方案一）

bool EnQueue(SqQueue &Q, ElemType x){
    if((Q.rear+1)%MaxSize == Q.front)        //队满
        return false;
    Q.data[Q.rear] = x;                      //将x插入队尾
    Q.rear = (Q.rear + 1) % MaxSize;         //队尾指针加1取模

    return true;
}

循环队列——出队：只能让队头元素出队

//出队，删除一个队头元素，用x返回
bool DeQueue(SqQueue &Q, ElemType &x){
    if(Q.rear == Q.front)              //队空报错
        return false;  

    x = Q.data[Q.front];
    Q.front = (Q.front + 1) % MaxSize; //队头指针后移动

    return true;
}

循环队列——获得队头元素

bool GetHead(SqQueue &Q, ElemType &x){
    if(Q.rear == Q.front)              //队空报错
        return false;  

    x = Q.data[Q.front];
    return true;
}

方案二: 不牺牲存储空间，设置size
定义一个变量 size用于记录队列此时记录了几个数据元素，初始化 size = 0，进队成功 size++，出队成功size--，根据size的值判断队满与队空

队满条件：size == MaxSize

队空条件：size == 0

# define MaxSize 10;     
typedef struct{
    ElemType data[MaxSize];   
    int front, rear;        
    int size;               //队列当前长度
}SqQueue;

//初始化队列
void InitQueue(SqQueue &Q){
    Q.rear = Q.front = 0;
    size = 0;
}

方案三: 不牺牲存储空间，设置tag
定义一个变量 tag，tag = 0 --最近进行的是删除操作；tag = 1 --最近进行的是插入操作；

每次删除操作成功时，都令tag = 0；只有删除操作，才可能导致队空；
每次插入操作成功时，都令tag = 1；只有插入操作，才可能导致队满；
队满条件：Q.front == Q.rear && tag == 1
队空条件：Q.front == Q.rear && tag == 0

# define MaxSize 10;     
typedef struct{
    ElemType data[MaxSize];   
    int front, rear;        
    int tag;               //最近进行的是删除or插入
}SqQueue;

3.2.2.3 知识回顾