搜索与图论(一)

一、DFS与BFS

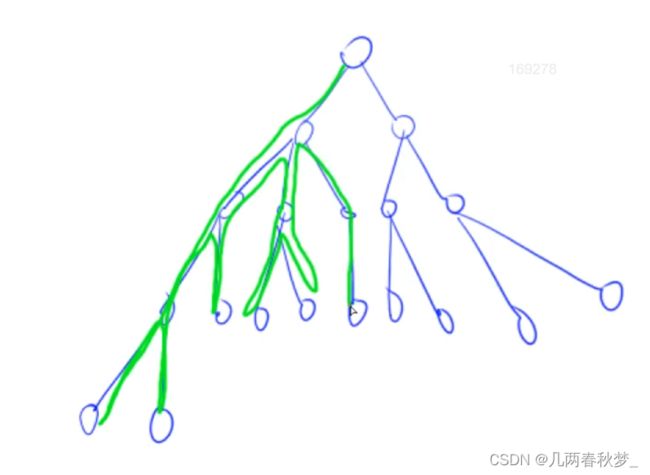
1.1深度优先搜索(DFS)

DFS不具有最短性

//排列数字问题
#include
using namespace std;

const int N = 10;
int n;
int path[N];
bool st[N];

void dfs(int u)
{
    if(u == n)
    {
        for(int i = 0;i < n;i++) printf("%d",path[i]);
        puts("");
        return;
    }
    for(int i =1;i <= n;i++)
    {
        if(!st[i])
        {
            path[u] = i;
            st[i] = true;
            dfs(u + 1);
            st[i] = false;
        }
    }
}
int main()
{
    cin>>n;
    dfs(0);
    return 0;
}

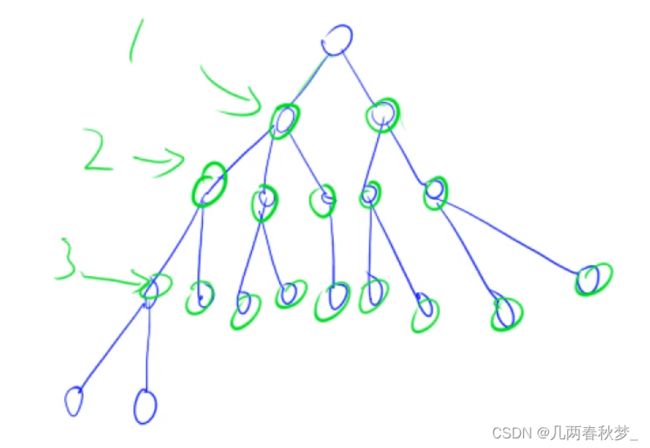
1.2宽度优先搜索(BFS)

一层一层搜索，可以搜到最短路。

 

 

//走迷宫问题
#include
#include
#include
#include
using namespace std;

typedef pair PII;

const int N = 110;

int n,m;
int g[N][N];
int d[N][N];
PII q[N * N];

int bfs()
{
    int hh = 0,tt = 0;
    q[0] = {0,0};

    //初始化为-1
    memset(d,-1,sizeof d);
    d[0][0] = 0;

    //定义头的向量
    int dx[4] = {-1,0,1,0},dy[4] = {0,1,0,-1};

    while(hh <= tt)
    {
        auto t = q[hh ++];

        for(int  i = 0; i< 4;i++)
        {
            int x = t.first + dx[i],y = t.second + dy[i];
            if(x >=0 && x < n && y >= 0 && y < m && g[x][y] ==0 && d[x][y] == -1)
            {
                d[x][y] = d[t.first][t.second] + 1;
                q[++ tt] = {x,y};
            }
        }
    }
    return d[n - 1][m - 1];
}

int main()
{
    cin>>n>>m;

    for(int  i = 0;i < n;i++)
        for(int j = 0;j < m;j++)
            cin>>g[i][j];

    cout<

二、树与图的遍历

2.1树与图的深度优先遍历

#include
using namespace std;

int n,m;
//h存的是n个链表的链表头
//e存的是所有的结点值
//ne存的是每个节点的next指针
int h[N],e[M],ne[M],idx;
bool st[N];

void dfs(int u)
{
    stu[u] = true; //标记一下，已经被搜过了
    
    for(int i = h[u];i != -1;i = ne[i])
    {
        int j = e[i];
        if(!st[j]) dfs(j);
    }
}

2.2树与图的广度优先遍历

 

int n,m;
int h[N],e[N],ne[N],idx;
//d是距离,q是队列
int d[N],q[N];

//插入函数
void add(int a,int b)
{
    e[idx] = b,ne[idx],ne[idx] = h[a],h[a] = idx++;
}
int bfs()
{
    //定义队头队尾
    int hh = 0,tt = 0;
    q[0] = 1;
    
    memset(d,-1,sizeof d);
    
    d[1] = 0;
    
    while(hh <= tt)
    {
        int t = q[hh ++];
        for(int i = h[t];i != -1;i = ne[i])
        {
            int j = e[i];
            if(d[j] == -1)
            {
                d[j] = d[t] + 1;
                q[++ tt] = j;
            }
        }
    }
    return d[n];
}

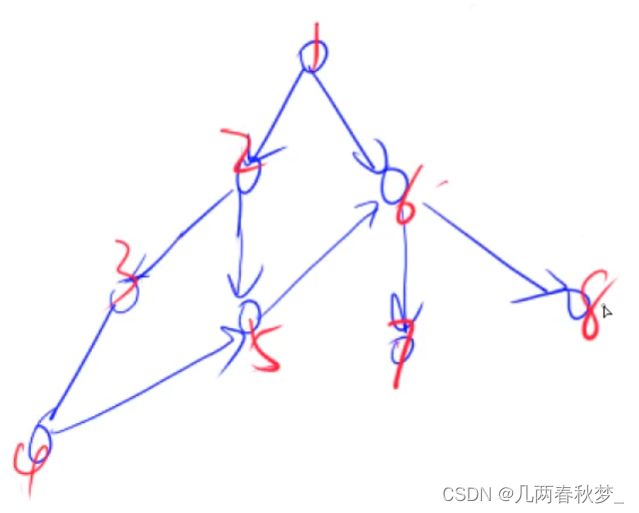
三、拓扑排序

适用于有向图

 

#include
#include
#include

using namespace std;

const int N = 100010;

int n,m;
int h[N],e[N],ne[N],idx;
//q为队列,d为存储的入度
int q[N],d[N];

void add(int a,int b)
{
    e[idx] = b,ne[idx] = h[a],h[a] = idx++;
}

bool topsort()
{
    int hh = 0,tt = -1;

    for(int i =1;i <= n;i++)
    {
        if(!d[i])
            q[++tt] = i;
    }
    while(hh <= tt)
    {
        int t = q[hh++];

        for(int i = h[t];i!=-1;i = ne[i])
        {
            int j = e[i];
            d[j]--;
            if(d[j] == 0) q[++tt] = j;
        }
    }
    return tt == n-1;
}
int main()
{
    cin>>n>>m;

    memset(h,-1,sizeof h);

    for(int  i = 0;i < m;i++)
    {
        int a,b;
        cin>>a>>b;
        add(a,b);
    }
    if(topsort())
    {
        for(int i =0;i < n;i++) printf("%d",q[i]);
        puts("");
    }
    else{
        puts("-1");
    }

    return 0;
}