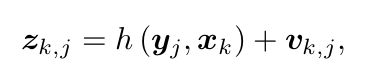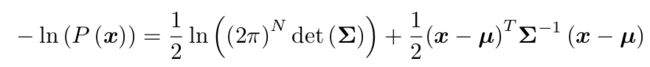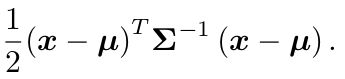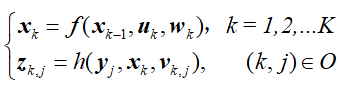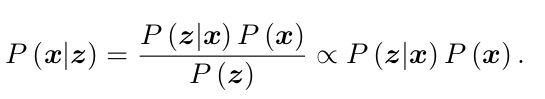视觉slam十四讲 学习笔记-4

目录

相机模型

单目相机

双目相机

状态估计问题

 实践：点云拼接

批量状态估计问题

非线性最小二乘 

实践

-----------作业------------

---

相机模型

单目相机

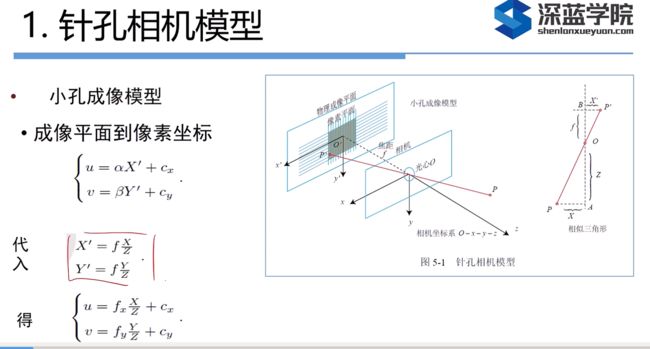
  下图中：u 轴向右与 x 轴平行，v轴向下与 y 轴平行，像素坐标系与成像平面之间,相差了一个缩放和一个原点的平移。我们设像素坐标在 u 轴上缩放了 α 倍,在 v 上缩放了 β 倍。同时,原点平移了 [c x , c y ] T 。式3中： 

 这四个参数称为相机的内参（即表示的是缩放和平移）一般来说是相近或者数值一样。

 上图中的矩阵形式乘开即为展开形式，其中矩阵即为内参矩阵K 

 上图中：中间的量组成的矩阵称为相机的内参数矩阵K，世界坐标记为Pw，中的括号就是先将世界坐标系转化为相机的坐标系，然后乘以K内参矩阵再进行一次转换。这里分别是齐次和非齐次的表示方式。

畸变：其中k和p为参数，属于相机的内参 。

我们知道平面上的任意一点 p 可以用笛卡尔坐标表示为 [x, y] T , 也可以把它写成极坐标的形式[r, θ] T ,其中 r 表示点 p 离坐标系原点的距离,θ 表示和水平轴的夹角。径向畸变可看成坐标点沿着长度方向发生了变化 δr, 也就是其距离原点的长度发生了变化。切向畸变可以看成坐标点沿着切线方向发生了变化,也就是水平夹角发生了变化 δθ。

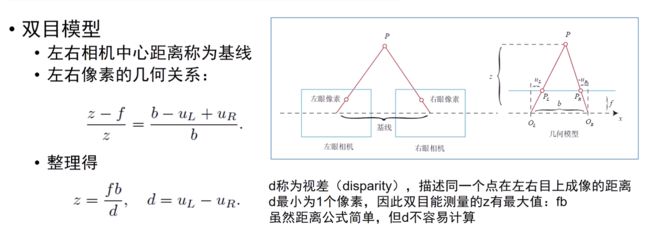
双目相机

非线性优化

牛顿法  ：

牛顿法，高斯-牛顿法_gauss newton method_Yemiekai的博客-CSDN博客

LM-Levenberg–Marquardt algorithm ：（1:16:20）【一起读书】视觉SLAM十四讲 第6讲（中）矩阵向量求导思路总结 非线性最小二乘若干解法原理推导分析 这讲准备了很久 希望对大家有帮助_哔哩哔哩_bilibili

最小二乘的引出： （书P123）

对于某一次观测的观测方程：

 

噪声项：，其中Q为一个3*3协方差矩阵。

由于噪声的存在当我们知道xy的值时候去推算出的z，z就满足正态分布（因为如果没有噪声，推出来的z肯定是一个准确的值，由于有一个满足高斯分布的噪声，那么推出来的值也是满足下面的高斯分布的）：

 

 上式中：P为条件概率，表示的是在条件xy下z所发生的概率，这里的z是一个变量，我们需要去求的，我们要去求得z取某个值的时候使得p最大（这样的含义就是在xy观测下，最有可能的位姿为z）。这个公式表示，在给定机器人位姿和地图特征的条件下，观测数据的条件概率服从（这里的等式理解为服从更好）以预测函数h为均值、以观测噪声协方差矩阵Q为协方差矩阵的高斯分布。（因为噪声是服从高斯分布的，h函数具体是一个值）

考虑一个任意的高维高斯分布 x ∼ N (μ, Σ)---μ为均值，Σ为协方差，它的概率密度函数展开形式为:

取对数

 因为我们要求x取什么值时P最大，前半部分和x无关，所以这里只看这一部分

所以要求P(x)最大，就是求这部分的最小值

 对于高斯分布，将其带入上式化简部分：

即要求这部分的最小值

 

 

-------------------------------------------------------------

首先回顾一下两个方程，第一个是运动方程，第二个是观测方程，参考：

x表示机器人（相机）的实际坐标；y表示某一个特征点的实际坐标；u表示内部传感器得出来的运动量（比如我们可以使用位移传感器和IMU测得 ）；z也表示传感器的感知的观测量（第j个特征点的坐标）；w、v表示噪声。

我们从这篇极大似然估计的博客可以得知：我们可以通过最大化似然函数来求出最接近实际的参数值。我们这里就是要通过u和v的值来尽可能估计出x和y的值。

我们将所有待估计的变量放在一个“状态变量”中（即将x和y放在一起作为x考虑）:

我们对机器人状态的估计,就是求已知输入数据 u 和观测数据 z 的条件下,计算上面的状态x的条件概率分布，记为P(x|z,u)

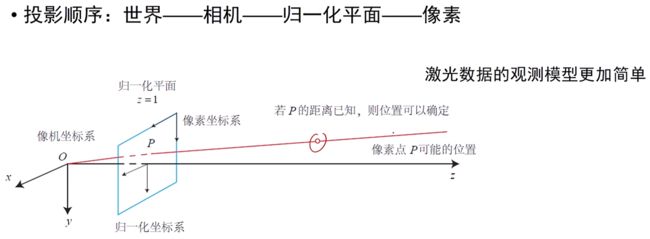
特别地，当我们没有测量运动的传感器，只有一张张的图像时，即只考虑观测方程带来的数据时，相当于估计 P (x|z) 的条件概率分布。

利用贝叶斯法则可以转化一下研究对象，最后是正比于P(z|x)P(x)的（因为分母部分与待估计的状态 x 无关，所以不考虑分母部分）：

 这时我们要求的使得P(x|z)最大化就变成了：最大化似然和先验的乘积。

如果此时在不清楚机器人具体的位姿的情况下，不知道P(x)，就只能尽可能考虑最大化P(z|x)。

最大化高斯分布：

考虑一个高斯分布：，他的概率密度函数为：

 这里我们对其进行取负对数从而方便求导（因为我们要找最大值）：

 因为对数是一个单调函数，所以并不会改变最值的位置，而这里我们取得是负对数，所以我们之前求最大就变成了求最小。

 实践：点云拼接

opencv的cmake配置：

cmake_minimum_required( VERSION 2.8 )
project( imageBasics )

# 添加c++ 11标准支持
set( CMAKE_CXX_FLAGS "-std=c++11" )

# 寻找OpenCV库
find_package( OpenCV 3 REQUIRED )
# 添加头文件
include_directories( ${OpenCV_INCLUDE_DIRS} )

add_executable( imageBasics imageBasics.cpp )
# 链接OpenCV库
target_link_libraries( imageBasics ${OpenCV_LIBS} )

程序中我们演示了： 图像读取、显示、像素遍历、拷贝、赋值等。

#include 
#include 
using namespace std;

#include 
#include 

int main ( int argc, char** argv )
{
    // 读取argv[1]指定的图像
    cv::Mat image;
    image = cv::imread ( argv[1] ); //cv::imread函数读取指定路径下的图像
    // 判断图像文件是否正确读取
    if ( image.data == nullptr ) //数据不存在,可能是文件不存在
    {
        cerr<<"文件"< ( y );  // row_ptr是第y行的头指针
        for ( size_t x=0; x time_used = chrono::duration_cast>( t2-t1 );
    cout<<"遍历图像用时："<

终端运行：

cd build
cmake ..
make
./imageBasics ../ubuntu.png 

安装点云：

sudo apt-get install libpcl-dev
sudo apt-get install pcl-tools 

运行：

cd joinMap
build/joinMap  #执行可执行程序，需要在pose.txt文件下执行这个命令
pcl_viewer map.pcd   #使用pcl显示点云

批量状态估计问题

这部分没太懂

非线性最小二乘 

实践：ceres和g2o

ceres安装：

Ubuntu18.04安装Ceres，图文详解_振华OPPO的博客-CSDN博客_ceres安装

使用ceres拟合曲线（求解最小二乘问题）

以下代码最重要的部分就是：struct代价函数和构建最小二乘问题

ceres的使用说明：

1. 定义 Cost Function 模型，代码中对应的是CURVE_FITTING_COST。方法是去书写一个类（这里用的struct结构体）,并在类中定义带模板参数的 () 运算符。

2. 调用 AddResidualBlock 将误差项添加到目标函数中。由于优化需要梯度,我们有若
干种选择:(1)使用 Ceres 的自动求导(Auto Diff);(2)使用数值求导(Numeric Diff);(3)自行推导解析的导数形式,提供给 Ceres。其中自动求导在编码上是最方便的,于是我们就使用自动求导

3. 自动求导需要指定误差项和优化变量的维度。这里的误差则是标量（ 误差为y-exp(ax^2+bx+c)  ），维度只有一维。优化的是 a, b, c 三个量,维度为 3。于是,在自动求导类的模板参数中设定变量维度为1，3对应代码

4. 设定好问题后,调用 solve 函数进行求解。你可以在 option 里配置(非常详细的)优
化选项。例如,我们可以选择使用 Line Search 还是 Trust Region,迭代次数,步长
等等。读者可以查看 Options 的定义,看看有哪些优化方法可选,当然默认的配置已
经可以用在很广泛的问题上了。

我这样理解：我们最终要求得是函数这个式子的最小值，其中y代表的是在x取值的情况下实际随机生成的点的y的值（生成y是有高斯噪声的，也就是有误差的），我们代码中生成的100数据中每个x都对应一个具有误差的y值。要对整个式子求最小，其中x,y是一系列已知的值，a,b,c是变量，所以对a,b,c进行求导，也就是待优化的值，所以维度为<1,3>。

代码思路：我们要通过ceres来拟合，即设置abc的值分别为1 2 1。我们再通过产生的100点产生的值加上随机产生高斯噪声生成100个y，从而生成了100对(x,y)，当然这些x,y都是在这个图像附近的（因为噪声的存在）。随后我们通过构建这100个点的值构建最小二乘：，从而来求出最接近1，2，1的abc的值。如果sigma噪声的值更小，那么拟合也会更加准确。

#include 
#include 
#include 
#include 

using namespace std;

// 代价函数的计算模型
struct CURVE_FITTING_COST
{
    CURVE_FITTING_COST ( double x, double y ) : _x ( x ), _y ( y ) {}
    // 残差的计算
    template 
    bool operator() (
        const T* const abc,     // 模型参数，有3维
        T* residual ) const     // 残差
    {
        residual[0] = T ( _y ) - ceres::exp ( abc[0]*T ( _x ) *T ( _x ) + abc[1]*T ( _x ) + abc[2] ); // y-exp(ax^2+bx+c)
        return true;
    }
    const double _x, _y;    // x,y数据
};

int main ( int argc, char** argv )
{
    double a=1.0, b=2.0, c=1.0;         // 真实参数值
    int N=100;                          // 数据点
    double w_sigma=1.0;                 // 噪声Sigma值
    cv::RNG rng;                        // OpenCV随机数产生器
    double abc[3] = {0,0,0};            // abc参数的估计值

    vector x_data, y_data;      // 数据

    cout<<"generating data: "< ( 
                new CURVE_FITTING_COST ( x_data[i], y_data[i] )
            ),
            nullptr,            // 核函数，这里不使用，为空
            abc                 // 待估计参数
        );
    }

    // 配置求解器
    ceres::Solver::Options options;     // 这里有很多配置项可以填，比如迭代次数、高斯牛顿、LM等，下面一行设置了linear_solver_type的类型
    options.linear_solver_type = ceres::DENSE_QR;  // 增量方程如何求解，这里使用的是QR方法，还有其他：cholesky、功能梯度法等等
    options.minimizer_progress_to_stdout = true;   // 输出到cout

    ceres::Solver::Summary summary;                // 优化信息
    chrono::steady_clock::time_point t1 = chrono::steady_clock::now();
    ceres::Solve ( options, &problem, &summary );  // 开始优化
    chrono::steady_clock::time_point t2 = chrono::steady_clock::now();
    chrono::duration time_used = chrono::duration_cast>( t2-t1 );
    cout<<"solve time cost = "<

g2o安装

首先对g2o进行编译安装：g2o安装_zdb呀的博客-CSDN博客_g2o安装

然后将slambook_master中的g2o_curve_fitting中的代码复制出来打开，记得cmake_modules一并复制，因为里面的.cmake文件需要寻找依赖。

-----------作业------------

1图像去畸变

cmake_minimum_required(VERSION 3.2)
project(ch4)

#注意opencv支持c++11以上
set(CMAKE_CXX_FLAGS "-std=c++11")

find_package(OpenCV 3.2 REQUIRED)
include_directories(${OPENCV_INCLUDE_DIRS})
add_executable(ch4 undistort_image.cpp)
target_link_libraries(ch4 ${OpenCV_LIBS})

//
// Created by 高翔 on 2017/12/15.
//

#include 
#include 
#include "cmath"
using namespace std;

string image_file = "/home/gzy/ROS/slam/ch4/test.png";   // 请确保路径正确

int main(int argc, char **argv) {

    // 本程序需要你自己实现去畸变部分的代码。尽管我们可以调用OpenCV的去畸变，但自己实现一遍有助于理解。
    // 畸变参数
    double k1 = -0.28340811, k2 = 0.07395907, p1 = 0.00019359, p2 = 1.76187114e-05;
    // 内参
    double fx = 458.654, fy = 457.296, cx = 367.215, cy = 248.375;

    cv::Mat image = cv::imread(image_file,0);   // 图像是灰度图，CV_8UC1
    int rows = image.rows, cols = image.cols;
    cv::Mat image_undistort = cv::Mat(rows, cols, CV_8UC1);   // 去畸变以后的图

    // 计算去畸变后图像的内容
    for (int v = 0; v < rows; v++)
        for (int u = 0; u < cols; u++) {

            double u_distorted = 0, v_distorted = 0;
            // TODO 按照公式，计算点(u,v)对应到畸变图像中的坐标(u_distorted, v_distorted) (~6 lines)
            // start your code here
            double x_rescale_one=(u-cx)/fx;
            double y_rescale_one=(v-cy)/fy;
            double r=sqrt(pow(x_rescale_one,2)+ pow(y_rescale_one,2));
            double x_distort=x_rescale_one*(1+k1*pow(r,2)+k2*pow(r,4))
                             +2*p1*x_rescale_one*y_rescale_one
                             +p2*(pow(r,2)+2*pow(x_rescale_one,2));
            double y_distort=y_rescale_one*(1+k1*pow(r,2)+k2*pow(r,4))
                             +p1*(pow(r,2)+2*pow(y_rescale_one,2))
                             +2*p2*x_rescale_one*y_rescale_one;
            u_distorted=fx*x_distort+cx;
            v_distorted=fy*y_distort+cy;


            // end your code here

            // 赋值 (最近邻插值)
            if (u_distorted >= 0 && v_distorted >= 0 && u_distorted < cols && v_distorted < rows) {
                image_undistort.at(v, u) = image.at((int) v_distorted, (int) u_distorted);
            } else {
                image_undistort.at(v, u) = 0;
            }
        }

    // 画图去畸变后图像
    cv::imshow("image undistorted", image_undistort);
    cv::waitKey();

    return 0;
}

2双目视差

这里也使用了vscode试了试：具体操作看第一节的笔记

cmake_minimum_required(VERSION 3.2)
project(ch4_2)

set(CMAKE_CXX_STANDARD 14)

#Eigen
include_directories(usr/include/Eigen)

#opencv
find_package(OpenCV 3 REQUIRED)
include_directories(${OPENCV_INCLUDE_DIRS})

#pangolin
find_package(Pangolin REQUIRED)
include_directories(${Pangolin_INCLUDE_DIRS})

add_executable(ch4_2 disparity.cpp)
target_link_libraries(ch4_2 ${OpenCV_LIBRARIES})
target_link_libraries(ch4_2 ${Pangolin_LIBRARIES})

 这部分代码中：书写部分在start  your code 到end your code

//
// Created by 高翔 on 2017/12/15.
//

#include 
#include 
#include 
#include 
#include 

using namespace std;
using namespace Eigen;

// 文件路径，如果不对，请调整
string left_file = "/home/gzy/ROS/slam/ch4-2-vs/left.png";
string right_file = "/home/gzy/ROS/slam/ch4-2-vs/right.png";
string disparity_file = "/home/gzy/ROS/slam/ch4-2-vs/disparity.png";

// 在panglin中画图，已写好，无需调整
void showPointCloud(const vector> &pointcloud);

int main(int argc, char **argv) {

    // 内参
    double fx = 718.856, fy = 718.856, cx = 607.1928, cy = 185.2157;
    // 间距
    double b = 0.573;

    // 读取图像
    cv::Mat left = cv::imread(left_file, 0);
    cv::Mat right = cv::imread(right_file, 0);
    cv::Mat disparity = cv::imread(disparity_file, 0); // disparty 为CV_8U,单位为像素

    // 生成点云
    vector> pointcloud;

    // TODO 根据双目模型计算点云
    // 如果你的机器慢，请把后面的v++和u++改成v+=2, u+=2
    for (int v = 0; v < left.rows; v++)
        for (int u = 0; u < left.cols; u++) {

            Vector4d point(0, 0, 0, left.at(v, u) / 255.0); // 前三维为xyz,第四维为颜色

            // start your code here (~6 lines)
            // 根据双目模型计算 point 的位置
            double x=(u-cx)/fx;
            double y=(v-cy)/fy;
            double dispar=disparity.at(v,u);  //读出来(v,u)这点的视差dispar
            double depth=fx*b/dispar;   //这里使用的是z=fb/d的这个公式，这里公式的z就对应着depth


            //还原真实坐标，只需将归一化坐标的xy乘以depth即可，z方向的就是depth
            point[0]=x*depth;
            point[1]=y*depth;
            point[2]=depth;
            pointcloud.push_back(point);


            // end your code here
        }

    // 画出点云
    showPointCloud(pointcloud);
    return 0;
}

void showPointCloud(const vector> &pointcloud) {

    if (pointcloud.empty()) {
        cerr << "Point cloud is empty!" << endl;
        return;
    }

    pangolin::CreateWindowAndBind("Point Cloud Viewer", 1024, 768);
    glEnable(GL_DEPTH_TEST);
    glEnable(GL_BLEND);
    glBlendFunc(GL_SRC_ALPHA, GL_ONE_MINUS_SRC_ALPHA);

    pangolin::OpenGlRenderState s_cam(
            pangolin::ProjectionMatrix(1024, 768, 500, 500, 512, 389, 0.1, 1000),
            pangolin::ModelViewLookAt(0, -0.1, -1.8, 0, 0, 0, 0.0, -1.0, 0.0)
    );

    pangolin::View &d_cam = pangolin::CreateDisplay()
            .SetBounds(0.0, 1.0, pangolin::Attach::Pix(175), 1.0, -1024.0f / 768.0f)
            .SetHandler(new pangolin::Handler3D(s_cam));

    while (pangolin::ShouldQuit() == false) {
        glClear(GL_COLOR_BUFFER_BIT | GL_DEPTH_BUFFER_BIT);

        d_cam.Activate(s_cam);
        glClearColor(1.0f, 1.0f, 1.0f, 1.0f);

        glPointSize(2);
        glBegin(GL_POINTS);
        for (auto &p: pointcloud) {
            glColor3f(p[3], p[3], p[3]);
            glVertex3d(p[0], p[1], p[2]);
        }
        glEnd();
        pangolin::FinishFrame();
        usleep(5000);   // sleep 5 ms
    }
    return;
}

4高斯牛顿法