【数据结构】链表(单链表实现+详解+原码)
目录
前言
链表
链表的概念及结构
链表的分类
1. 单向或者双向
2.带头或不带头
3.循环或非循环
单链表的实现
打印链表
申请结点
尾插
头插
尾删
头删
指定位置后面插入
指定位置删除
查找
销毁链表
完整代码
力扣链表OJ
顺序表和链表的区别
前言
上一章我们学到了顺序表，实现了顺序表的增删查改。
当然也发现了顺序表存在的一些优点与缺陷，我们再来回顾一下：
优点：
- 支持随机访问，可以通过下标来直接访问。
- 可以排序。
缺点：
- 中间/头部的插入删除，时间复杂度为O(N)
- 增容需要申请新空间，拷贝数据，释放旧空间。会有不小的消耗。
- 增容一般是呈2倍的增长，势必会有一定的空间浪费。
所以为了弥补这些缺点就有了链表，那么什么是链表呢？
链表
链表的概念及结构
概念：链表是一种物理存储结构上非连续、非顺序的存储结构，数据元素的逻辑顺序是通过链表中的指针链接次序实现的 。
只根据文字描述还是比较抽象的，直接上图来观察：
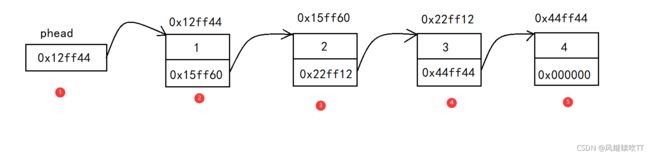
图中：2.3.4.5都是结构体，称之为结点，与顺序表不同的是，链表中的每个结点不是只单纯的存一个数据。而是一个结构体，结构体成员包括一个所存的数据，和下一个结点的地址。另外，顺序表中的地址是连续的，而链表中结点的地址是随机分配的。
那链表是怎样运行的呢？
图中的phead指针中存放的是第一个结点的地址，那么根据指着地址我们就可以找到这个结构体，又因为这个结构体中存放了下一个结构体的地址，所以又可以找到第二个结构体，循环往复就可以找到所有的结点，直到存放空地址的结构体。
注：图中的箭头实际上是不存在的，这里只是为了能够方便理解。
注意：
- 从图中可以看出，链式结构在逻辑上是连续的，但在物理上不一定连续。
- 现实中的结点一般都是从堆上申请出来的。
- 从堆上申请的空间，是按照一定的策略来分配的，两次申请的空间可能连续，也可能不连续。
链表的分类
实际中链表的结构非常多样，以下情况组合起来就有8种链表结构：
1. 单向或者双向
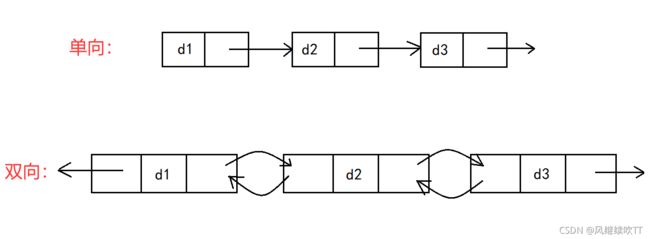
2.带头或不带头
3.循环或非循环
虽然有这么多的链表的结构，但是我们实际中最常用还是两种结构：
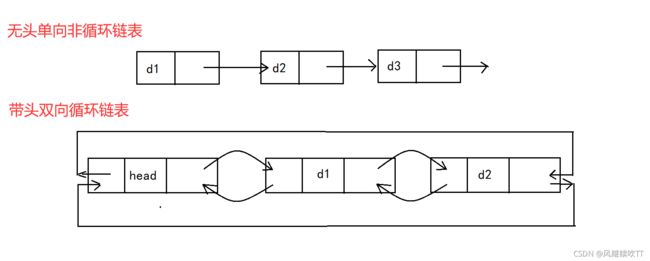1. 无头单向非循环链表：结构简单，一般不会单独用来存数据。实际中更多是作为其他数据结构的子结构，如哈希桶、图的邻接表等等。另外这种结构在笔试面试中出现很多。
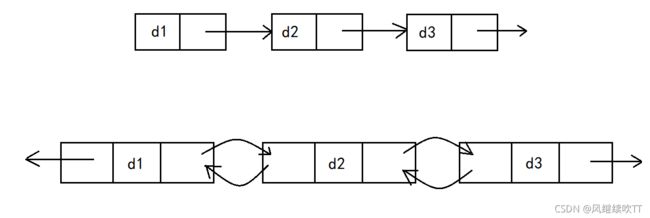
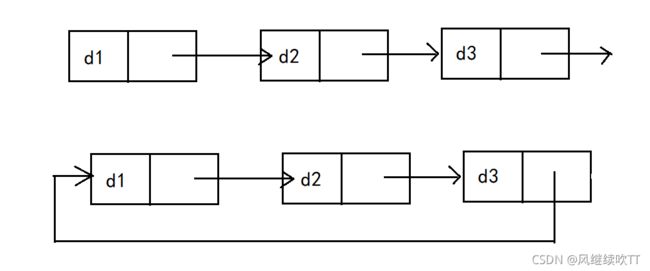
2. 带头双向循环链表：结构最复杂，一般用在单独存储数据。实际中使用的链表数据结构，都是带头双向循环链表。另外这个结构虽然结构复杂，但是使用代码实现以后会发现结构会带来很多优势，实现反而简单了，后面我们代码实现了就知道了。
单链表的实现
#pragma once
#include
#include
#include
typedef int SLTDataType;
typedef struct SListNode
{
SLTDataType data;
struct SListNode* next;//存放下一个结点的地址
}SListNode;
//打印链表
void SListPrint(SListNode* phead);
//申请结点
SListNode* SListBuyNode(SLTDataType x);
//因为我们是通过一个指针指向该链表的头结点，同时因为在进行插入删除操作时可能改变链表的头结点，所下面的参数需传二级指针
//尾插
void SListPushBack(SListNode** pphead, SLTDataType x);
//头插
void SListPushFront(SListNode** pphead, SLTDataType x);
//尾删
void SListPopBack(SListNode** pphead);
//头删
void SListPopFront(SListNode** pphead);
//查找
SListNode* SListFind(SListNode* phead, SLTDataType x);
//指定位置后面插入
void SListInsert(SListNode** pphead, SListNode* pos, SLTDataType x);
//指定位置后面删除
void SListErase(SListNode** pphead, SListNode* pos);
//销毁链表
void SListDestory(SListNode** pphead);
打印链表
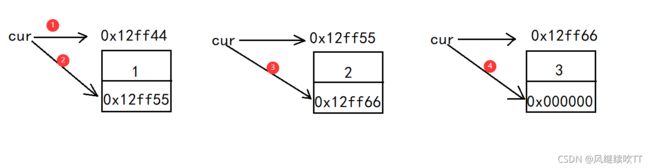
在顺序表中是通过下标来访问每个元素，链表与顺序表不同，在访问到本结点的数据之后，需通过该结点存放的地址找到下一个结点。
//打印链表
void SListPrint(SListNode* phead)
{
SListNode* cur = phead;//一般不直接移动头指针，而是创建一个指针变量来移动
while (cur)//当指针为空时结束循环
{
printf("%d->", cur->data);//打印该结点的数据
cur = cur->next;//将指针指向下一个结点
}
printf("NULL\n");
}
申请结点
链表的每一个结点都是动态开辟(malloc)出来的，每一个结点的大小为该结构体的大小。
开辟成功后，要将结点存放的数据置为需要存放的值，结点存放的地址置为NULL。
//申请结点
SListNode* SListBuyNode(SLTDataType x)
{
SListNode* newnode = (SListNode*)malloc(sizeof(SListNode));
if (newnode == NULL)//判断结点是否开辟成功
{
perror("malloc:");
exit(-1);
}
newnode->data = x;
newnode->next = NULL;
return newnode;//返回结点地址
}尾插
因为不能根据下标访问元素(即不能随机访问)，当然我们也不知到最后一个结点的位置，所在尾插时，需要遍历找到最后一个结点的位置。
同时这里分为两种情况：
- 如果链表为空，则直接插入即可。
- 如果链表不为空，则需要找到尾结点再插入。
//尾插
void SListPushBack(SListNode** pphead, SLTDataType x)
{
assert(pphead);
SListNode* newnode = SListBuyNode(x);//申请结点
if (*pphead == NULL)//1.链表为空
{
*pphead = newnode;//直接将头结点置为需要插入的结点
}
else
{
SListNode* cur = *pphead;
while (cur->next)//找尾结点
{
cur = cur->next;
}
cur->next = newnode;//将尾结点中存放的地址置为插入结点的地址即可
}
}头插
头插相对来说比较简单，直接将申请结点的next置为头结点，然后将头结点改成申请结点即可
注：这里不需要考虑链表是否为空。
//头插
void SListPushFront(SListNode** pphead, SLTDataType x)
{
assert(pphead);
SListNode* newnode = SListBuyNode(x);
newnode->next = *pphead;//将申请结点中保存的地址置为头结点的地址
*pphead = newnode;//再将头结点向右移动
}尾删
同尾插一样，我们也不知道尾结点的地址，所以需要先找到尾结点。
同时这里需要考虑三种情况：
- 链表为空。
- 链表中只有一个结点。
- 链表中有一个以上结点。
//尾删
void SListPopBack(SListNode** pphead)
{
//1.链表为空不能删除结点,且该指针不能为空
assert(*pphead && phead);
//2.链表中只有一个结点，直接释放该结点，然后将结点置为NULL
if ((*pphead)->next == NULL)
{
free(*pphead);
*pphead = NULL;
return;
}
//3.链表中有一个以上结点，先找尾结点，释放掉尾结点,置为NULL
// 但这样还不够，因为倒数第二个结点还存有尾结点的地址，所以需要将他置为NULL
SListNode* cur = *pphead;//用来标记倒数第二个结点
SListNode* next = (*pphead)->next;//标记尾结点
while (next->next)
{
next = next->next;
cur = cur->next;
}
cur->next = NULL;//将倒数第二个结点中存的地址置为NULL
free(next);//释放尾结点
next = NULL;
}头删
头删也比较简单，相当于将头指针移动到第二个结点上。
这里分为两种情况：
- 链表为空。
- 链表不为空。
//头删
void SListPopFront(SListNode** pphead)
{
assert(*pphead && phead);//链表为空不能删除
SListNode* next = (*pphead)->next;//记录第二个结点的地址
free(*pphead);//释放头结点
*pphead = next;//将指针指向第二个结点
}
指定位置后面插入
这里在指定位置后面插入而不在前面插入是因为，在前面插入时需要找到插入位置前面的地址，而这样又会遍历一次链表，时间复杂度为O(N)，而在后面插入则直接插入即可，时间复杂度为O(1)。
//指定位置后面插入
void SListInsert(SListNode** pphead, SListNode* pos, SLTDataType x)
{
assert(pphead && pos);
SListNode* newnode = SListBuyNode(x);//申请结点
SListNode* next = pos->next;//找到插入位置的下一个结点的地址
pos->next = newnode;//插入结点
newnode->next = next;//连接到后面的链表
}// 在pos位置之前去插入一个节点
void SListInsert(SLTNode** pphead, ListNode* pos, SLTDateType x)
{
assert(pphead);
assert(pos);
ListNode* newnode = BuyListNode(x);
if (*pphead == pos)
{
newnode->next = *pphead;
*pphead = newnode;
}
else
{
// 找到pos的前一个位置
ListNode* posPrev = *pphead;
while (posPrev->next != pos)
{
posPrev = posPrev->next;
}
posPrev->next = newnode;
newnode->next = pos;
}
}
指定位置删除
这里在指定位置删除，而不在前面删除或者后面删除，是因为在头删和尾删时会遇到一些麻烦。
//指定位置删除
void SListErase(SListNode** pphead, SListNode* pos)
{
assert(pphead && pos);
if (*pphead == pos)//如果头结点是要删除的结点
{
*pphead = (*pphead)->next;
free(pos);
pos = NULL;
}
else
{
SListNode* cur = *pphead;
while (cur->next != pos)//找到要删除的结点
{
cur = cur->next;
}
cur->next = pos->next;//将需要删除的结点的上一个结点的next指向需要删除的下一个结点
free(pos);
pos = NULL;
}
}查找
根据提供的数据，在链表中遍历每个结点，若某个结点中的数据与之相同则返回该结点的地址；若没有找到则返回NULL。
//查找
SListNode* SListFind(SListNode* phead, SLTDataType x)
{
while (phead)
{
if (phead->data == x)
{
return phead;
}
phead = phead->next;
}
return NULL;
}销毁链表
保存下一个结点的地址，释放当前结点，再将指针指向下一个结点，释放下一个结点，直到链表为空。
//销毁链表
void SListDestory(SListNode** pphead)
{
assert(pphead);
while (*pphead)
{
SListNode* next = (*pphead)->next;
free(*pphead);
*pphead = next;
}
}完整代码
//打印链表
void SListPrint(SListNode* phead)
{
SListNode* cur = phead;
while (cur)
{
printf("%d->", cur->data);
cur = cur->next;
}
printf("NULL\n");
}
//申请结点
SListNode* SListBuyNode(SLTDataType x)
{
SListNode* newnode = (SListNode*)malloc(sizeof(SListNode));
if (newnode == NULL)
{
perror("malloc:");
exit(-1);
}
newnode->data = x;
newnode->next = NULL;
return newnode;
}
//销毁链表
void SListDestory(SListNode** pphead)
{
assert(pphead);
SListNode* cur = *pphead;
while (cur)
{
SListNode* next = cur->next;
free(cur);
cur = next;
}
*pphead = NULL;
}
//尾插
void SListPushBack(SListNode** pphead, SLTDataType x)
{
assert(pphead);
SListNode* newnode = SListBuyNode(x);
if (*pphead == NULL)
{
*pphead = newnode;
}
else
{
SListNode* cur = *pphead;
while (cur->next)
{
cur = cur->next;
}
cur->next = newnode;
}
}
//头插
void SListPushFront(SListNode** pphead, SLTDataType x)
{
assert(pphead);
SListNode* newnode = SListBuyNode(x);
newnode->next = *pphead;
*pphead = newnode;
}
//尾删
void SListPopBack(SListNode** pphead)
{
assert(*pphead && pphead);
if ((*pphead)->next == NULL)
{
free(*pphead);
*pphead = NULL;
return;
}
SListNode* cur = *pphead;
SListNode* next = (*pphead)->next;
while (next->next)
{
next = next->next;
cur = cur->next;
}
cur->next = NULL;
free(next);
next = NULL;
}
//头删
void SListPopFront(SListNode** pphead)
{
assert(*pphead && pphead);
SListNode* next = (*pphead)->next;
free(*pphead);
*pphead = next;
}
//查找
SListNode* SListFind(SListNode* phead, SLTDataType x)
{
while (phead)
{
if (phead->data == x)
{
return phead;
}
phead = phead->next;
}
return NULL;
}
//指定位置后面插入
void SListInsert(SListNode** pphead, SListNode* pos, SLTDataType x)
{
assert(pphead && pos);
SListNode* newnode = SListBuyNode(x);
SListNode* next = pos->next;
pos->next = newnode;
newnode->next = next;
}
//指定位置删除
void SListErase(SListNode** pphead, SListNode* pos)
{
assert(pphead && pos);
if (*pphead == pos)
{
*pphead = (*pphead)->next;
free(pos);
pos = NULL;
}
else
{
SListNode* cur = *pphead;
while (cur->next != pos)
{
cur = cur->next;
}
cur->next = pos->next;
free(pos);
pos = NULL;
}
}注：代码中的assert(*pphead)和assert(pphead)含义不相同！！！
assert(*pphead)表示的是链表不为空。
assert(pphead)表示的是参数二级指针不能为空，因为空指针不能解引用！
力扣链表OJ
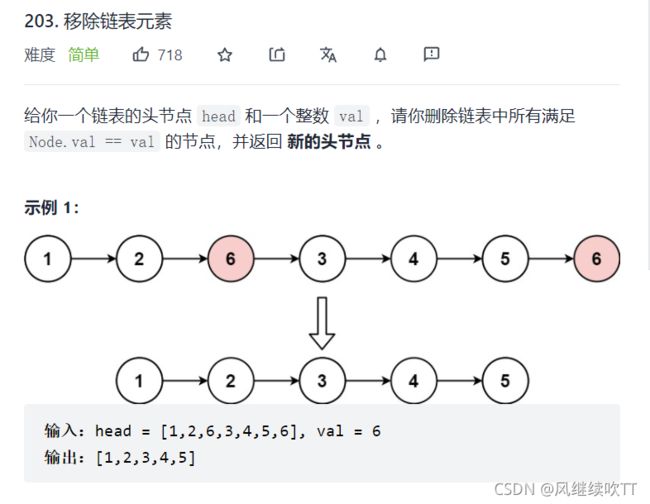
力扣---移除链表元素
思路：
与单链表的尾删类似，先找到需要删除的元素，将上一个结点的next指向该删除结点的next，
然后free掉当前结点。
当然这里也分为三种情况：
- 链表为空，返回NULL。
- 需要删除的结点为头结点，直接将头结点释放，将下一个结点作为头结点。
- 需要删除的结点在中，则使用常规方法。
代码如下：
typedef struct ListNode ListNode;//重命名，方便处理
struct ListNode* removeElements(struct ListNode* head, int val){
//1.链表为空，直接返回NULL
if(head == NULL)
{
return NULL;
}
//链表不为空
ListNode*cur =head;//标记需要删除结点
ListNode*prev = NULL;//标记需要删除结点的前一个结点
while(cur)
{
//找到需要删除的结点
if(cur->val==val)
{
//2.如果需要删除的结点为头结点
if(cur == head)
{
//将头指针指向第二个结点
head = head->next;
//释放头结点
free(cur);
cur = head;
}
//3.需要删除的结点在中间
else
{
//将前一个结点的next指向删除结点的next
prev->next = cur->next;
free(cur);
cur = prev->next;
}
}
//不是需要删除结点就向后移动
else
{
prev = cur;
cur = cur->next;
}
}
return head;
}顺序表和链表的区别
| 不同点 | 顺序表 | 链表 |
| 存储空间上 | 物理上一定连续 | 逻辑上连续，但物理上不一定连 续 |
| 随机访问 | 支持O(1) | 不支持：O(N) |
| 任意位置插入或者删除元 素 |
可能需要搬移元素，效率低O(N) | 只需修改指针指向 |
| 插入 | 动态顺序表，空间不够时需要扩 容 |
没有容量的概念 |
| 应用场景 | 元素高效存储+频繁访问 | 任意位置插入和删除频繁 |
| 缓存利用率 | 高 | 低 |