数据结构-第五章 树与二叉树-笔记
目录
关于几种常见二叉树的定义
构造二叉树的代码
二叉树的遍历方式汇总
线索二叉树
中序线索二叉树的构造
后序线索二叉树的构造:
先序线索二叉树的构造
在中序线索二叉树中寻找中序后继、中序线索二叉树的遍历
在中序线索二叉树中寻找中序前驱、中序线索二叉树的逆向遍历
在先序线索二叉树中寻找先序前驱和先序后继
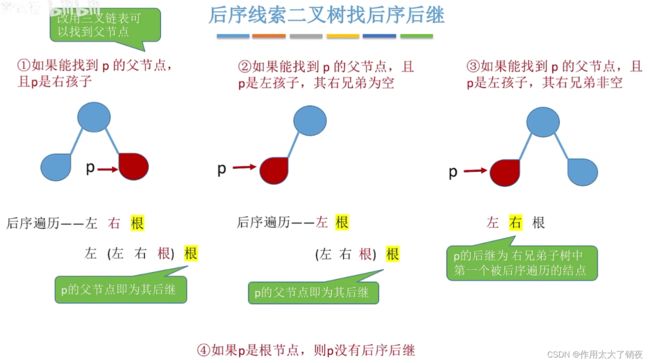
在后序线索二叉树中寻找后序前驱和后序后继
5.3.4 课后习题
19、计算二叉树的带权路径长度(WPL)
20、将表达式树转换为中缀表达式
二叉排序树的构造和插入
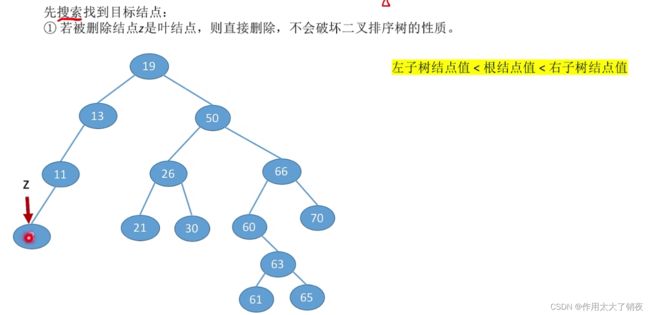
二叉排序树的删除
情况一:
情况二:
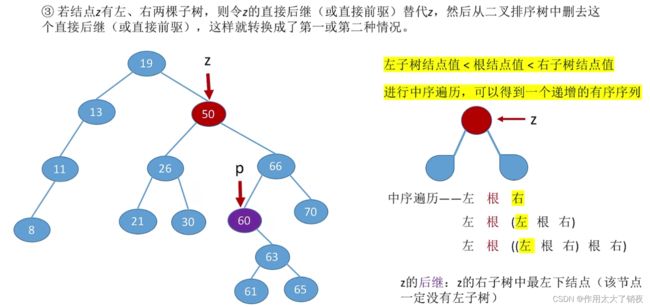
情况三(较为复杂):
实现代码
二叉排序树的查找
查找成功长度计算示例:
查找失败长度计算示例:
查找效率分析:
平衡二叉树的插入与删除
画图
将二叉搜索树变平衡-代码
并查集
哈夫曼树的构造
深度(广度)优先生成树(森林)
习题-最近公共祖先
习题-判断一棵树是否为完全二叉树
习题-从前序与中序遍历构造二叉树
习题-从中序和后序遍历构造二叉树
习题-根据前序和后序遍历构造二叉树
习题-判断无向图G是否为一棵树
关于几种常见二叉树的定义
满二叉树:除最后一层无任何子节点外,每一层上的所有结点都有两个子结点的二叉树。
完全二叉树:一棵深度为k的有n个结点的二叉树,对树中的结点按从上至下、从左到右的顺序进行编号,如果编号为i(1≤i≤n)的结点与满二叉树中编号为i的结点在二叉树中的位置相同,则这棵二叉树称为完全二叉树。
二叉查找树/二叉排序树/二叉搜索树:首先它是二叉树,并且 左子树上所有结点的值 小于 它根结点的值,右子树上所有结点的值 大于 它根结点的值。
二叉平衡树/平衡二叉树:是 "平衡二叉搜索树" 的简称。首先它是 "二叉搜索树",其次,它是平衡的,即是它的每一个结点的左子树的高度和右子树的高度差至多为 1。
二叉判定树:二分查找所对应的判定树,既是二叉查找树,又是二叉平衡树。
【注】树不能为空,但二叉树可以为空,也就是说上面几种二叉树都可以为空。
构造二叉树的代码
平时写个关于二叉树的代码时,一般都难以找到例子验证,还得自己花费时间去构造一棵二叉树,于是我索性从力扣上扒了个构造二叉树的代码以供使用。
struct TreeNode {
int val;
TreeNode *left;
TreeNode *right;
TreeNode() : val(0), left(nullptr), right(nullptr) {}
TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
};
/*在此处编写函数*/
//输入示例:[1,null,2,3],其中null表示空节点
class Solution {
public:
void func(TreeNode* cur) {
if (cur == nullptr) return;
cout << cur->val;
func(cur->left);
func(cur->right);
}
};
void trimLeftTrailingSpaces(string& input) {
input.erase(input.begin(), find_if(input.begin(), input.end(), [](int ch) {
return !isspace(ch);
}));
}
void trimRightTrailingSpaces(string& input) {
input.erase(find_if(input.rbegin(), input.rend(), [](int ch) {
return !isspace(ch);
}).base(), input.end());
}
TreeNode* stringToTreeNode(string input) {
trimLeftTrailingSpaces(input);
trimRightTrailingSpaces(input);
input = input.substr(1, input.length() - 2);
if (!input.size()) {
return nullptr;
}
string item;
stringstream ss;
ss.str(input);
getline(ss, item, ',');
TreeNode* root = new TreeNode(stoi(item));
queue nodeQueue;
nodeQueue.push(root);
while (true) {
TreeNode* node = nodeQueue.front();
nodeQueue.pop();
if (!getline(ss, item, ',')) {
break;
}
trimLeftTrailingSpaces(item);
if (item != "null") {
int leftNumber = stoi(item);
node->left = new TreeNode(leftNumber);
nodeQueue.push(node->left);
}
if (!getline(ss, item, ',')) {
break;
}
trimLeftTrailingSpaces(item);
if (item != "null") {
int rightNumber = stoi(item);
node->right = new TreeNode(rightNumber);
nodeQueue.push(node->right);
}
}
return root;
}
int main() {
string line;
while (getline(cin, line)) {
TreeNode* root = stringToTreeNode(line);
/*在此处调用函数*/
Solution().func(root);
cout << endl;
}
return 0;
} 二叉树的遍历方式汇总
之前有总结过,详情查看此处:
(4条消息) 2021.9.27 二叉树的递归与非递归遍历方式汇总_作用太大了销夜的博客-CSDN博客
线索二叉树
中序线索二叉树的构造
struct TreeNode {
int val;
TreeNode *left;
TreeNode *right;
int ltag = 0;//ltag为0时表示指向的是左孩子,为1时表示结点的前驱
int rtag = 0;//rtag为0时表示指向的是右孩子,为1时表示结点的后继
};
TreeNode* pre = nullptr; //全局变量pre,指向结点cur的前驱
//访问结点cur,并建立前驱和后继
void visit(TreeNode* cur)
{
//如果cur的左指针为空,就建立前驱线索,将其指向pre
//当cur是中序的第一个结点时,pre刚好是nullptr
if (cur->left == nullptr)
{
cur->left = pre;
cur->ltag = 1;
}
//如果pre的右指针为空,就建立后继线索,将其指向cur
if (pre != nullptr && pre->right == nullptr)
{
pre->right = cur;
pre->rtag = 1;
}
pre = cur; //每次访问完当前结点之后,pre都更新,指向了当前结点
}
//中序线索化二叉树,本质上是对二叉树做一次中序遍历
void InThread(TreeNode* cur)
{
if (cur == nullptr) return;
InThread(cur->left);
visit(cur);
InThread(cur->right);
}
//建立线索二叉树的主函数
void CreatInThread(TreeNode* root)
{
pre = nullptr; //pre初始化为空
if (root != nullptr) //若二叉树不为空,就将其线索化
{
InThread(root); //中序线索化二叉树
//由于当遍历到cur为最后一个结点时就退出循环了,因此最后一个结点的后继需要特殊处理
//根据pre = cur这条语句,最终pre指向的是二叉树的最后一个结点
pre->right = nullptr;
pre->rtag = 1;
}
}后序线索二叉树的构造:
struct TreeNode {
int val;
TreeNode *left;
TreeNode *right;
int ltag = 0;//ltag为0时表示指向的是左孩子,为1时表示结点的前驱
int rtag = 0;//rtag为0时表示指向的是右孩子,为1时表示结点的后继
};
TreeNode* pre = nullptr; //全局变量pre,指向结点cur的前驱
//访问结点cur,并建立前驱和后继
void visit(TreeNode* cur)
{
//如果cur的左指针为空,就建立前驱线索,将其指向pre
//当cur是后序的第一个结点时,pre刚好是nullptr
if (cur->left == nullptr)
{
cur->left = pre;
cur->ltag = 1;
}
//如果pre的右指针为空,就建立后继线索,将其指向cur
if (pre != nullptr && pre->right == nullptr)
{
pre->right = cur;
pre->rtag = 1;
}
pre = cur; //每次访问完当前结点之后,pre都更新,指向了当前结点
}
//后序线索化二叉树,本质上是对二叉树做一次后序遍历
void PostThread(TreeNode* cur)
{
if (cur == nullptr) return;
PostThread(cur->left);
PostThread(cur->right);
visit(cur);
}
//建立线索二叉树的主函数
void CreatPreThread(TreeNode* root)
{
pre = nullptr; //pre初始化为空
if (root != nullptr) //若二叉树不为空,就将其线索化
{
PostThread(root); //后序线索化二叉树
//由于当遍历到cur为最后一个结点时就退出循环了,因此最后一个结点的后继需要特殊处理
//根据pre = cur这条语句,最终pre指向的是二叉树的最后一个结点
if (pre->right == nullptr)
{
pre->rtag = 1;
}
}
}先序线索二叉树的构造
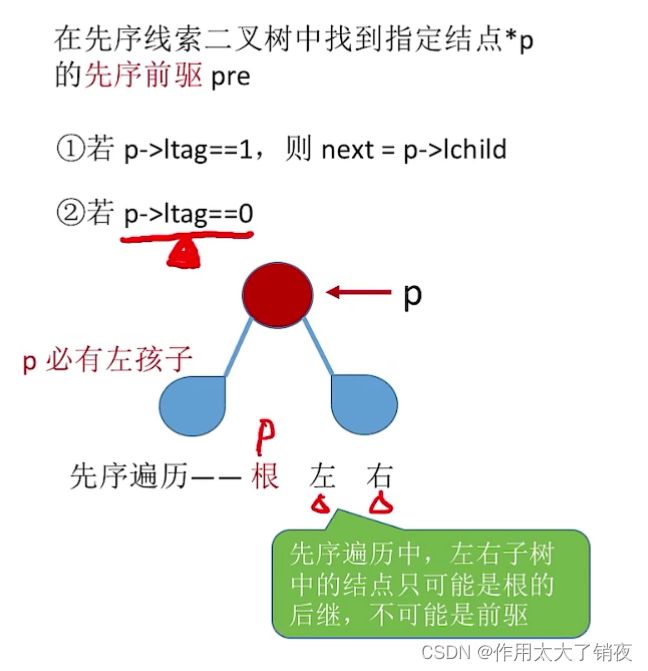
先序线索二叉树的构造大致与中序、后序相同,但是需要注意一点特殊情况,例如下图,在visit()函数访问完结点D之后,结点D的左指针指向了D的前驱B,但是后续的先序递归中,会再次进入结点D的左指针指向的结点B,导致无限循环。因此需要加一个特殊判断,当左指针不是线索时才能进入递归函数。
但是为什么只有先序线索二叉树的构造中会出现这种情况呢?因为“前驱线索的建立与当前节点cur有关,而后继线索的建立与先前节点pre有关”,在先序中,由于是先通过visit()函数建立了cur的前驱线索,因此在继续递归访问cur的左指针时可能会导致无限循环的问题;在中序中,由于是先访问了cur的左指针,再使用visit()函数建立cur的前驱线索和pre的后继线索,最后访问cur的右指针,因此不会出现循环的问题;在后序中是先访问了cur的左指针与右指针,后使用visit()函数建立cur的前驱线索和pre的后继线索,同样不会出现循环的问题。
struct TreeNode {
int val;
TreeNode *left;
TreeNode *right;
int ltag = 0;//ltag为0时表示指向的是左孩子,为1时表示结点的前驱
int rtag = 0;//rtag为0时表示指向的是右孩子,为1时表示结点的后继
};
TreeNode* pre = nullptr; //全局变量pre,指向结点cur的前驱
//访问结点cur,并建立前驱和后继
void visit(TreeNode* cur)
{
//如果cur的左指针为空,就建立前驱线索,将其指向pre
//当cur是先序的第一个结点时,pre刚好是nullptr
if (cur->left == nullptr)
{
cur->left = pre;
cur->ltag = 1;
}
//如果pre的右指针为空,就建立后继线索,将其指向cur
if (pre != nullptr && pre->right == nullptr)
{
pre->right = cur;
pre->rtag = 1;
}
pre = cur; //每次访问完当前结点之后,pre都更新,指向了当前结点
}
//先序线索化二叉树,本质上是对二叉树做一次先序遍历
void PreThread(TreeNode* cur)
{
if (cur == nullptr) return;
visit(cur);
if (cur->ltag == 0) //只有当左指针不是前驱线索时才递归左指针
{
PreThread(cur->left);
}
PreThread(cur->right);
}
//建立线索二叉树的主函数
void CreatPreThread(TreeNode* root)
{
pre = nullptr; //pre初始化为空
if (root != nullptr) //若二叉树不为空,就将其线索化
{
PreThread(root); //先序线索化二叉树
//由于当遍历到cur为最后一个结点时就退出循环了,因此最后一个结点的后继需要特殊处理
//根据根据pre = cur这条语句,最终pre指向的是二叉树的最后一个结点
if (pre->right == nullptr)
{
pre->rtag = 1;
}
}
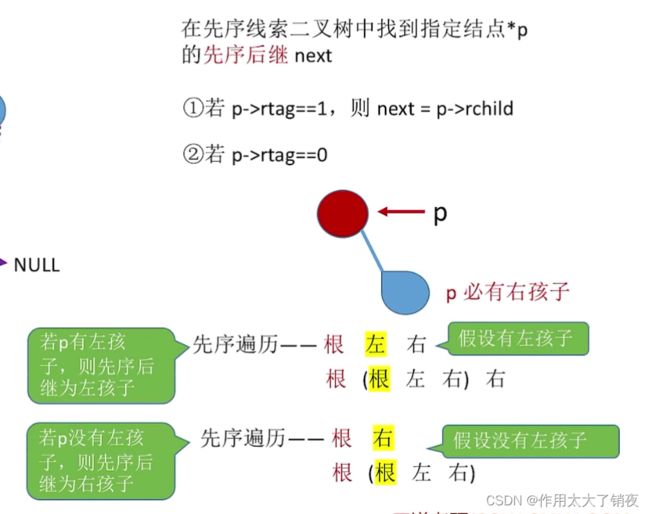
}在中序线索二叉树中寻找中序后继、中序线索二叉树的遍历
分析思路(注意这种逐层画图法只能将左子树、右子树展开,不能展开根):
//在以结点root为根节点的子树中,找到中序遍历时第一个被访问的结点,即子树的最左下结点(不一定是叶结点)
TreeNode* InThread_Firstnode(TreeNode* root)
{
//当左指针指向孩子节点时就不断寻找,由于只有线索才有可能指向nullptr,因此不用担心root = nullptr的问题
//我原本在想,既然要找中序遍历的第一个结点,那为什么不沿着ltag == 1递归呢?这是因为既然指针指向了孩子,那就不是线索指针
while (root->ltag == 0) root = root->left;
return root;
}
//在中序线索二叉树中找到结点cur的后继结点
TreeNode* InThread_Nextnode(TreeNode* cur)
{
//如果右指针指向孩子的话,就返回右子树的最左下结点(不一定是叶结点)
if (cur->rtag == 0) return InThread_Firstnode(cur->right);
//如果右指针是线索的话,直接返回即可
else return cur->right;
}
//对中序线索二叉树进行中序遍历
void InThread_order(TreeNode* root)
{
//注意it的初值不是root,而是中序遍历的第一个结点,即这颗树的最左下结点
for (TreeNode* it = InThread_Firstnode(root); it != nullptr; it = InThread_Nextnode(it))
{
cout << it->val << endl;
}
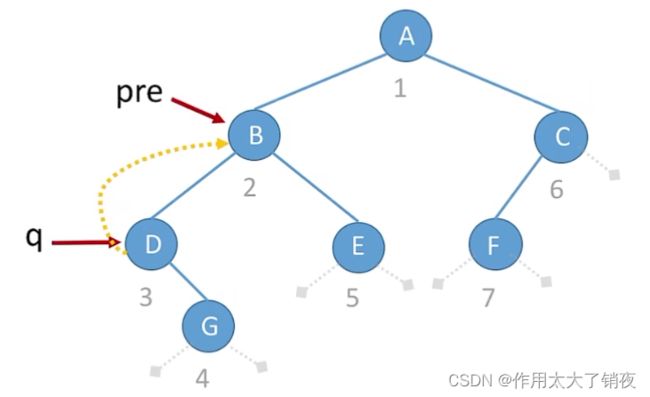
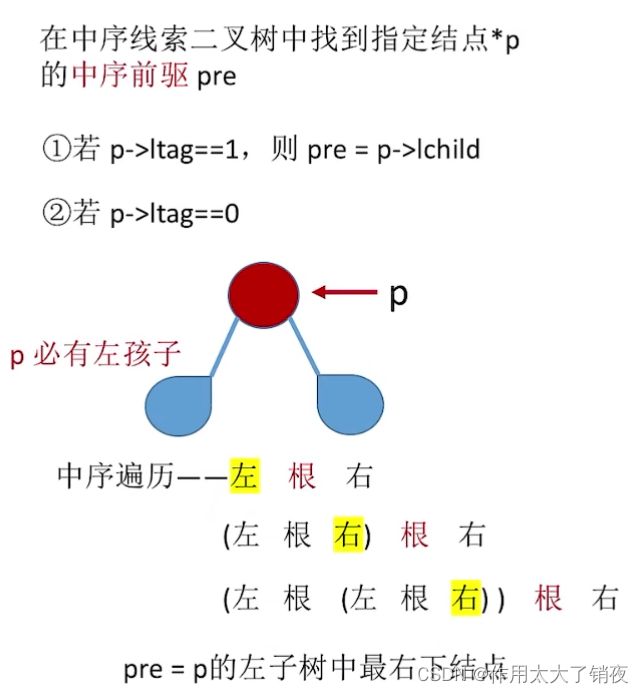
}在中序线索二叉树中寻找中序前驱、中序线索二叉树的逆向遍历
跟上述情况相反即可,分析思路(注意这种逐层画图法只能将左子树、右子树展开,不能展开根):
//在以结点root为根节点的子树中,找到中序遍历时最后一个被访问的结点,即子树的最右下结点
TreeNode* InThread_Lastnode(TreeNode* root)
{
//当右指针指向孩子节点时就不断寻找,由于只有线索才有可能指向nullptr,因此不用担心root = nullptr的问题
while (root->rtag == 0) root = root->right;
return root;
}
//在中序线索二叉树中找到结点cur的前驱结点
TreeNode* InThread_Prenode(TreeNode* cur)
{
//如果左指针指向孩子的话,就返回左子树的最右下结点
if (cur->ltag == 0) return InThread_Lastnode(cur->left);
//如果左指针是线索的话,直接返回即可
else return cur->left;
}
//对中序线索二叉树进行逆向中序遍历
void InThread_Revorder(TreeNode* root)
{
//注意it的初值不是root,而是中序遍历的最后一个结点,即这颗树的最右下结点
for (TreeNode* it = InThread_Lastnode(root); it != nullptr; it = InThread_Prenode(it))
{
cout << it->val << endl;
}
}
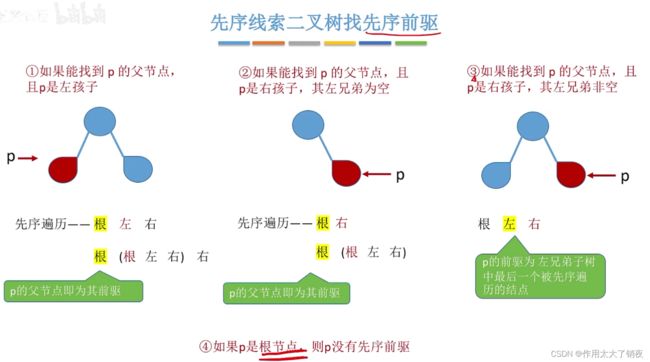
在先序线索二叉树中寻找先序前驱和先序后继
分析思路(注意这种逐层画图法只能将左子树、右子树展开,不能展开根):
但是只有左右指针的先序线索二叉树,是无法找到某个结点的先序前驱的:
如果先序线索二叉树在结点中有指向父节点的指针,那么有以下几种情况:
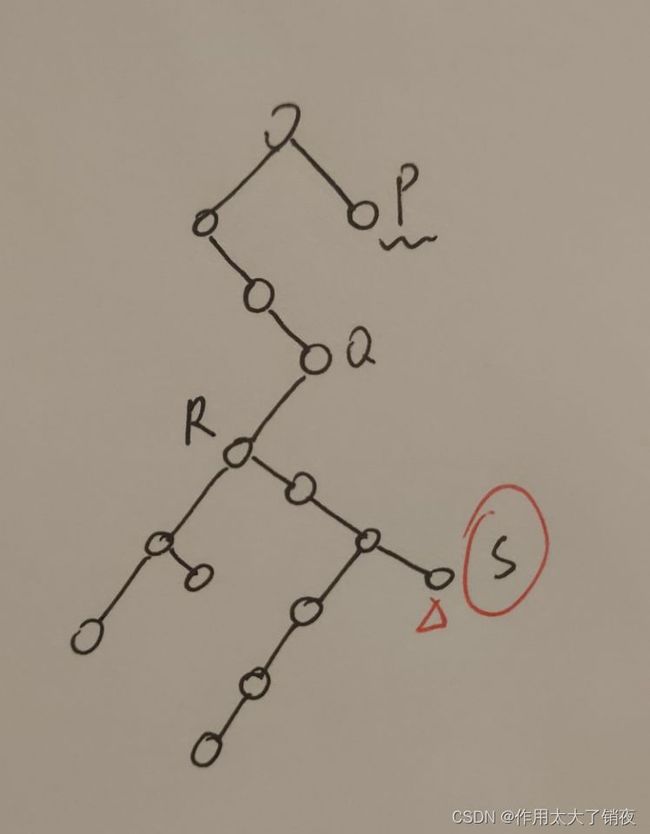
前两种用逐层画图法挺好理解的,第三种有点绕,结点P的前驱结点就是左兄弟子树中最后一个被先序遍历访问的结点,反正就是对左兄弟子树使用一遍先序遍历,然后找到最后一个结点,如下图:
P的先序前驱就是结点S。
代码实现逻辑为:在P的左兄弟子树中先向右下找到最后一个没有右孩子的结点Q,但是发现Q还有左孩子,按照先序遍历的规则目标结点应该在Q的左子树中,于是向Q的左子树中向左下找到第一个有右孩子的结点R(如果都没有右孩子,那就是找到最左下的结点即可),按照先序遍历的规则,目标结点应该存在R的右子树中,因此可以不用进入R的左子树,直接在R的右子树中找到最后一个没有右孩子的结点S,由于S没有左孩子,因此搜寻到此结束,S就是P的先序前驱结点。
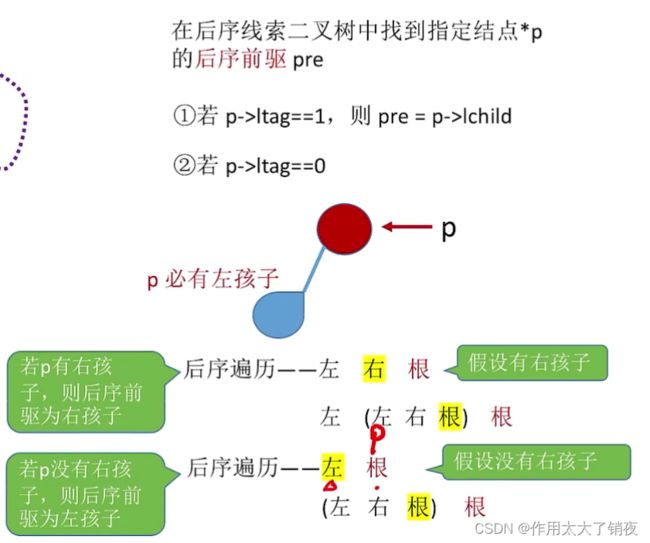
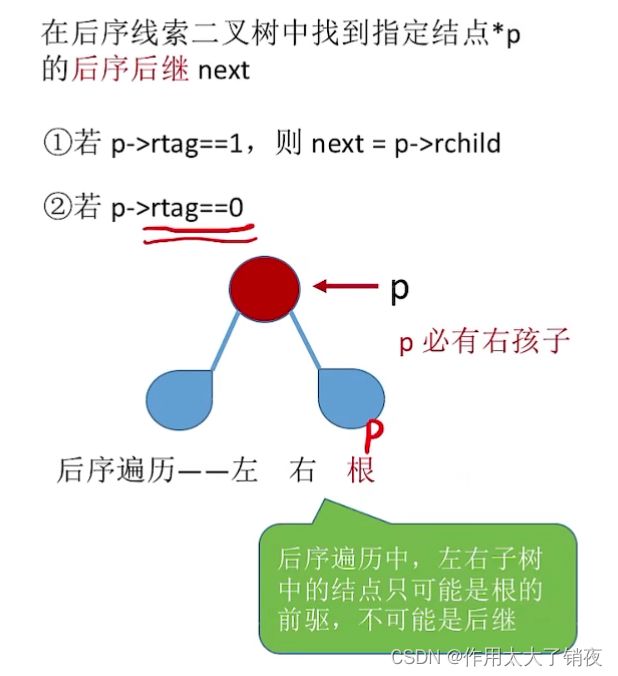
在后序线索二叉树中寻找后序前驱和后序后继
分析思路(注意这种逐层画图法只能将左子树、右子树展开,不能展开根):
同样,只有左右指针的后序线索二叉树,是无法找到某个结点的后序后继的:
如果有指向父节点的指针的话,就是以下情况:
情况分析都与上述寻找先序线索二叉树的先序前驱是一样的,第三种情况中,结点P的后继结点就是右兄弟子树中第一个被后序遍历访问的结点,反正就是对右兄弟子树使用一遍后序遍历,然后找到第一个结点,例子如下:
结点P的后序后继就是结点S。
代码实现逻辑为:在结点P的右兄弟结点子树中不断向左下找到第一个没有左孩子的结点Q,但是发现结点Q还有右孩子,根据后序遍历的规则,目标结点应该位于结点Q的右子树中,因此再向Q的右子树中不断向右下找到第一个有左孩子的结点R(如果都没有左孩子,就直接找到最右下的结点即可),根据后续遍历的规则,目标结点应该位于结点R的左子树中,因此不用理会R的右子树,直接在R的左子树中向左下找到第一个没有左孩子的结点S,由于S没有右孩子,因此搜寻到此结束,结点S就是P的后序后继结点。
5.3.4 课后习题
19、计算二叉树的带权路径长度(WPL)
一开始没搞懂带权路径长度的意思,是这样的:
struct TreeNode {
int weight;
TreeNode* left = nullptr;
TreeNode* right = nullptr;
TreeNode(int v)
{
weight = v;
}
};
int tree_wpl = 0;
void caculatewpl(TreeNode* root, int depth)
{
if (root == nullptr) return;
if (root->left == nullptr && root->right == nullptr)
{
tree_wpl += root->weight * depth;
}
caculatewpl(root->left, depth + 1);
caculatewpl(root->right, depth + 1);
}20、将表达式树转换为中缀表达式
我想复杂了。。想着判断是不是操作符、专门用一个全局变量来记录所得的表达式,但写的有点乱。实际上这题不用那么复杂,表达式的中序列加上必要的序号即为等价的中缀表达,并且非叶结点肯定是操作符,叶结点肯定是操作数,因此在二叉树的中序遍历上修改即可。
void turnmid(BTree* root, int depth)
{
if (root == nullptr) return;
//若为叶结点,说明是操作数,直接输出即可
if (root->left == nullptr && root->right == nullptr)
{
cout << root->data;
}
//非叶结点,说明是操作符
else
{
//整个表达式的最外圈不用加括号,只有每个子树的表达式外面需要加括号,当深度depth大于1时就说明是子树
if (depth > 1) cout << "(";
turnmid(root->left, depth + 1);
cout << root->data; //输出操作符
turnmid(root->right, depth + 1);
if (depth > 1) cout << ")";
}
}二叉排序树的构造和插入
王道的写法中,树的节点是以引用的形式作为参数传入函数,对引用类型的参数修改就相当于对原来的变量的修改。
而我这里是将节点以指针的形式作为参数传入函数,因此每次递归都需要返回一个节点,否则在递归中节点所产生的变化不会作用在原树上。
typedef struct TreeNode
{
int val;
TreeNode* left, * right;
}TreeNode;
//二叉排序树的插入
TreeNode* BST_insert(TreeNode* cur, int v)
{
if (cur == NULL) //如果cur为空,就在这里建立一个新树,新插入的v作为根节点
{
cur = (TreeNode*)malloc(sizeof(TreeNode));
cur->val = v;
cur->left = NULL;
cur->right = NULL;
}
else if (v < cur->val) //如果v小于cur的值,就插入到cur的左子树中
{
cur->left = BST_insert(cur->left, v);
}
else if (v > cur->val) //如果v大于cur的值,就插入到cur的右子树中
{
cur->right = BST_insert(cur->right, v);
}
//如果v等于cur的值,插入失败(这里不做任何动作)
return cur; //操作完毕后返回当前节点cur
}
//中序遍历
void midprint(TreeNode* cur)
{
if (cur == NULL) return;
midprint(cur->left);
printf("%d ", cur->val);
midprint(cur->right);
}
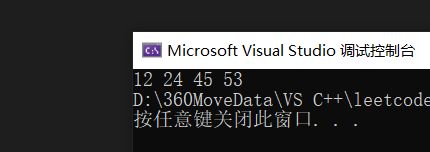
int main()
{
int a[10] = { 45, 24, 53, 45, 12, 24 };
//二叉排序树的构造
TreeNode* root = NULL; //根节点一定要初始化为NULL,不然在BST_insert()函数中没法构造新树
for (int i = 0; i < 6; i++)
{
root = BST_insert(root, a[i]); //每次插入都要用根节点接收返回的新树
}
midprint(root);
return 0;
}
建立之后的二叉排序树的中序遍历:
二叉排序树的删除
情况一:
情况二:
例如上图中删除60这个结点时,由于60只有右子树,没有左子树,所以可以直接让60的右子树代替60成为66的左子树
情况三(较为复杂):
①利用直接后继结点
例如删除图中的结点Z,可以用Z的直接后继结点,即右子树中的最左下结点P,来替代Z的位置,同时由于P是右子树中的最左下结点,所以其肯定没有左子树,因此在移动结点P后可以参照情况二将P的右子树直接替代P的位置。
②利用直接前驱结点
例如删除图中的结点Z,可以用Z的直接前驱结点,即左子树中的最右下结点30,来替代Z的位置,同时由于30是左子树中的最左下结点,所以其肯定没有右子树,因此在移动30后可以参照情况二将30的左子树直接替代P的位置(当然,该图中30没有左子树)
实现代码
之前实现,一直以为挺简单的,动手写了下发现确实有点难
题目链接:
450. 删除二叉搜索树中的节点 - 力扣(LeetCode)
官方的题解:
代码:
class Solution {
public:
TreeNode* deleteNode(TreeNode* root, int key) {
if (root == nullptr) return nullptr;
//如果root的值大于key,说明p位于root的左子树中,对左子树进行修改
if (root->val > key)
{
root->left = deleteNode(root->left, key);
return root;
}
//如果root的值小于key,说明p位于root的右子树中,对右子树进行修改
if (root->val < key)
{
root->right = deleteNode(root->right, key);
return root;
}
//如果root就是要删除的结点p,则判断几种不同的删除情况
if (root->val == key)
{
//如果root是叶结点,则直接删除即可
if (!root->left && !root->right)
{
return nullptr;
}
//如果root只有左子树,直接删除root,返回左子树
if (root->left && !root->right)
{
return root->left;
}
//如果root只有右子树,直接删除root,返回右子树
if (!root->left && root->right)
{
return root->right;
}
//如果root同时存在左子树和右子树
if (root->left && root->right)
{
//找到root的后继节点post
TreeNode* post = root->right;
while (post->left)
{
post = post->left;
}
//先在右子树中删除post(当然不是实际上的删除,毕竟post待会还要用)
root->right = deleteNode(root->right, post->val);
//用post代替root,返回post
post->left = root->left;
post->right = root->right;
return post;
}
}
return root;
}
};二叉排序树的查找
查找成功长度计算示例:
查找失败长度计算示例:
在计算前可以先画出这些代表查找失败的矩形,注意对于一个结点来说查找失败分为小于和大于两种情况
查找效率分析:
由于一棵高度为h的树,查找到最下一层结点需要比较h次,因此查找成功的效率不会超过树的高度h,因此:
平衡二叉树的插入与删除
画图
(18条消息) 平衡二叉树插入操作的详细过程图解_土豆西瓜大芝麻的博客-CSDN博客_平衡二叉树插入
(18条消息) 平衡二叉树的删除_poixao的博客-CSDN博客_平衡二叉树的删除
将二叉搜索树变平衡-代码
题目链接:1382. 将二叉搜索树变平衡 - 力扣(LeetCode)
直接用旋转的方法手撕AV树的话非常麻烦,这里算是特解了,先得到二叉搜索树的中根遍历序列,然后再根据这个中根遍历序列构造一棵平衡的二叉树。
这种方法只适用于二叉搜索树,与其说是调整,不如说是直接重构成一棵平衡树。
class Solution {
public:
vector Inorder;
void get_Inorder(TreeNode* cur)
{
if (cur == nullptr) return;
get_Inorder(cur->left);
Inorder.push_back(cur->val);
get_Inorder(cur->right);
}
TreeNode* build(int left, int right)
{
if (left > right) return nullptr;
int mid = (left + right) / 2;
TreeNode* cur = new TreeNode(Inorder[mid]);
cur->left = build(left, mid - 1);
cur->right = build(mid + 1, right);
return cur;
}
TreeNode* balanceBST(TreeNode* root) {
get_Inorder(root);
root = build(0, Inorder.size() - 1);
return root;
}
}; 并查集
查看此处:(14条消息) 2021.11.21 力扣-省份数量-并查集练习_作用太大了销夜的博客-CSDN博客
哈夫曼树的构造
原以为构造哈夫曼树还得用到并查集,没想到不用,只要一开始将各个节点按照权值升序排好就方便操作了,这里假设一开始已经排序。
/*
b 1
a 3
c 4
d 10
f 12
g 13
e 15
*/
typedef struct TreeNode
{
char info; //节点信息
int weight; //节点权值
char code[10]; //编码
TreeNode* left, * right;
}TreeNode;
//对各个字符进行编码
void encode(TreeNode* cur, char curcode[])
{
if (cur == NULL) return;
if (cur->left == NULL && cur->right == NULL) //遇到叶子节点,就确定其编码
{
strcpy(cur->code, curcode);
return;
}
char sl[10], sr[10];
strcpy(sl, curcode);
strcat(sl, "0"); //转入左子树,编码就加"0"
encode(cur->left, sl);
strcpy(sr, curcode);
strcat(sr, "1"); //转入右子树,编码就加"1"
encode(cur->right, sr);
}
//先序遍历,输出各个字符的编码
void printcode(TreeNode* cur)
{
if (cur == NULL) return;
if (cur->left == NULL && cur->right == NULL) printf("%c:%s ", cur->info, cur->code);
printcode(cur->left);
printcode(cur->right);
}
int main()
{
TreeNode* a[7];
//先假设原来的各个节点都已经升序排好
for (int i = 0; i < 7; i++)
{
TreeNode* tmp = (TreeNode*)malloc(sizeof(TreeNode));
scanf("%c %d",&tmp->info, &tmp->weight);
getchar(); //清除一个回车符,防止回车符被下一个info读入
tmp->left = NULL;
tmp->right = NULL;
a[i] = tmp;
}
//将权值最小的两棵树a[i]和a[i+1]合并后,再按升序添加回数组中,最终数组的最后一个节点就是根节点
for (int i = 0; i < 6; i++)
{
TreeNode* lchild = a[i];
TreeNode* rchild = a[i + 1];
TreeNode* tmp = (TreeNode*)malloc(sizeof(TreeNode));
tmp->weight = lchild->weight + rchild->weight;
tmp->left = lchild;
tmp->right = rchild;
int j;
//这么插入排序,排在第一个的不一定就是最小的元素,但前两个一定是最小的两个元素
for (j = i; j < 6 && a[j]->weight < tmp->weight; j++)
{
a[j] = a[j + 1];
}
a[j] = tmp;
}
char curcode[] = "";
encode(a[6], curcode); //对各个字符进行编码
printf("\n编码结果:\n");
printcode(a[6]); //先序遍历,输出各个字符的编码
return 0;
}以下图为例:
输出结果为:
深度(广度)优先生成树(森林)
(20条消息) 深度优先生成树和广度优先生成树_数据结构教程的博客-CSDN博客_深度优先生成树
习题-最近公共祖先
(19条消息) 2021.10.9 力扣-二叉树的最近公共祖先_作用太大了销夜的博客-CSDN博客
习题-判断一棵树是否为完全二叉树
上图中所说的“两个非空结点之间不可能有一个空结点”的意思是在任意两个非空结点之间(就算是不同层的非空结点也行)不可能有一个空结点。
代码如下:
#define n 100
bool func(TreeNode* root)
{
if (root == NULL) return true; //空树也是完全二叉树
TreeNode* que[n];
int front = 0, rear = 0;
que[rear++] = root;
rear %= n;
while (front != rear)
{
TreeNode* cur = que[front++];
front %= n;
if (cur != NULL) //如果结点非空,直接将其左孩子和右孩子入队
{
que[rear++] = cur->left; rear %= n;
que[rear++] = cur->right; rear %= n;
}
else //遇到空结点就退出
{
break;
}
}
while (front != rear) //查看队中剩余的元素是否还有非空结点
{
TreeNode* cur = que[front++];
front %= n;
if (cur != NULL) return false; //如果剩余元素中有非空结点,就说明不是完全二叉树
}
return true;
}
习题-从前序与中序遍历构造二叉树
(18条消息) 2021.10.6 力扣-从前序与中序遍历序列构造二叉树_作用太大了销夜的博客-CSDN博客
习题-从中序和后序遍历构造二叉树
(18条消息) 2021.10.5 力扣-从中序和后序遍历序列构造二叉树_作用太大了销夜的博客-CSDN博客
习题-根据前序和后序遍历构造二叉树
(18条消息) 2021.10.7 力扣-根据前序和后序遍历构造二叉树_作用太大了销夜的博客-CSDN博客
习题-判断无向图G是否为一棵树
思路如下:
#define maxsize 100
void dfs(int graph[][10], int n, int visited[], int cur, int* nodenum, int* edgenum)
{
visited[cur] = 1;
(*nodenum)++; //每遍历到一个点,点数+1
for (int i = 1; i <= n; i++)
{
if (graph[cur][i] == 1)
{
//我原本想着为什么不先遍历一遍图,找出图中的边数是否为2 * (n - 1)
//后来发现其实这一操作直接在dfs的过程中就可以完成
(*edgenum)++; //每遇到一条边,边数+1
if (!visited[i])
{
dfs(graph, n, visited, i, nodenum, edgenum);
}
}
}
}
void istree(int graph[][10], int n)
{
int visited[10] = { 0 };
int nodenum = 0, edgenum = 0; //点数和边数
dfs(graph, n, visited, 1, &nodenum, &edgenum);
printf("nodenum: %d edgenum: %d\n\n", nodenum, edgenum);
if (nodenum == n && edgenum == 2 * (n - 1))
{
printf("YES\n");
}
else
{
printf("NO\n");
}
}
int main()
{
int graph[10][10] = { 0 };
int n = 5;
graph[1][2] = 1; graph[2][1] = 1;
graph[1][3] = 1; graph[3][1] = 1;
graph[2][4] = 1; graph[4][2] = 1;
graph[4][5] = 1; graph[5][4] = 1;
//graph[1][4] = 1; graph[4][1] = 1;
printf("n: %d\n\n", n);
istree(graph, n);
return 0;
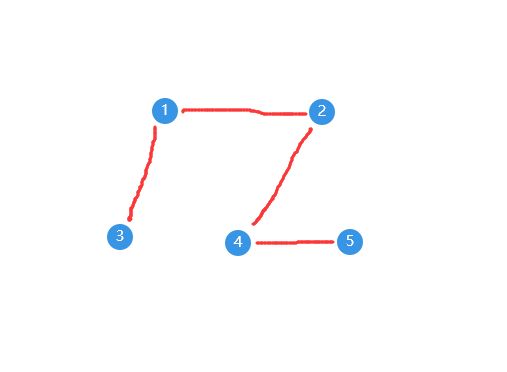
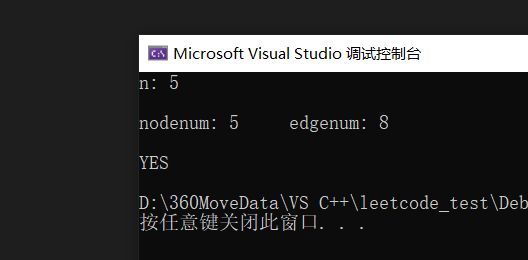
}例如对于下图来说:
代码的结果为:
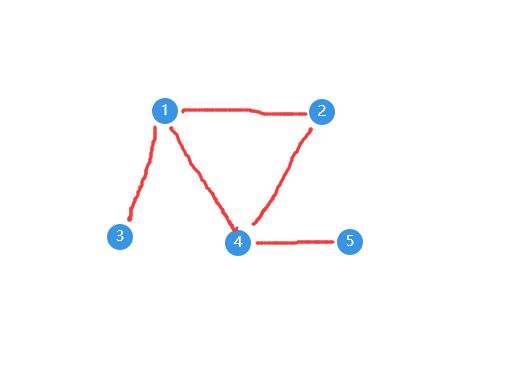
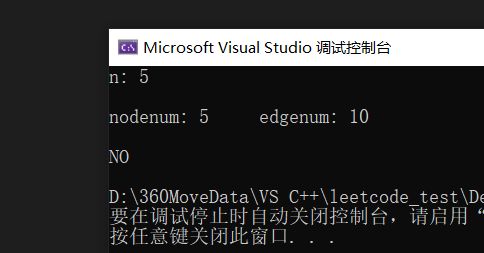
对于下图来说:
代码结果为: