【夜深人静学习数据结构与算法 | 第十二篇】动态规划——背包问题
目录
前言:
01背包问题:
二维数组思路:
一维数组思路:
总结:
前言:
在前面我们学习动态规划理论知识的时候,我就讲过要介绍一下背包问题,那么今天我们就来讲解一下背包问题。
在这里我们只介绍01背包,至于分组背包和混合背包这种的已经属于竞赛级别的了,难度过高,我们在这里就不学习了。
【夜深人静学数据结构与算法 | 第十篇】动态规划_我是一盘牛肉的博客-CSDN博客
01背包问题:
该问题的背景是一个背包和一组物品,每个物品都有自己的价值和重量。目标是选择一些物品放入背包中,使得放入的物品总重量不超过背包的容量,且总价值最大化。
具体来说,给定 n 个物品,其重量分别为 w1, w2, …, wn,价值分别为 v1, v2, …, vn,以及一个背包的容量 W。如何在不超过背包容量的情况下拿到的物品可以实现价值最大?
我们还是严格按照动态规划五步走来确定解题思路:
二维数组思路:
1.dp数组的含义以及下标的含义:dp[i][j]的含义为把[0,i]的物品放到容量为j的背包里 的最大价值。
- 如果不放当前第 i 个物品,那么此时的最大价值就是 dp[ i-1] [ j ]
- 如果放当前第 i 个物品,那么此时的最大价值就是 dp [ i-1 ][ j-weight[i]] + value[i]
2.递推公式的推导:dp[i][j]= max(dp[ i-1] [ j ],dp [ i-1 ][ j-weight[i]] + value[i])
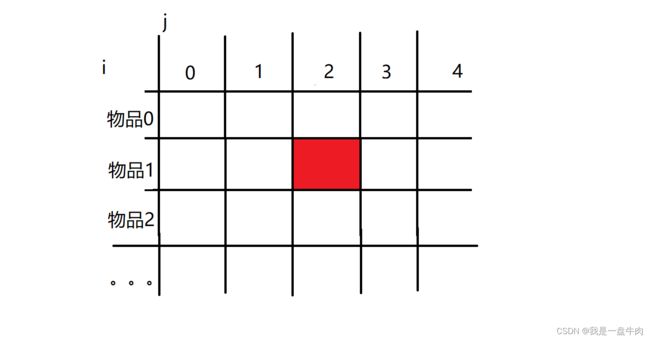
3.dp数组的初始化:对于dp数组应该如何初始化,我们可以用画图的方式来表示一下dp数组
如果此时我们动态规划到红色的这块区域,由dp数组的公式 dp[i][j]= max(dp[ i-1] [ j ],dp [ i-1 ][ j-weight[i]] + value[i])我们可以知道,这块红色的区域的值一定是由整个数组的左上角区域慢慢推过来的。因此在开始我们就要把左上角的全部初始化,防止出现减不了的情况:
而具体的初始化值,我们简单想一想就可以知道,当背包容量为0的时候,就装不了东西,那么最大价值就是0,那么我们就把竖行的值初始化为0,也就是dp[i][0]初始化为0,横行就是始终装物品0,那么只要背包的容量大于物品0的容量,最大的价值就是dp[0][j]=value.(物品0)。
4.dp数组遍历顺序:对于二维数组的这两个for循环,无论是先便利背包还是物品都是可以的。
那么用一个例子来实现一下动态规划:
#include
#include
using namespace std;
// 定义物品结构体,包含重量和价值
struct Item {
int weight;
int value;
};
int knapsack(int W, vector- & items) {
int size = items.size();
vector
> dp(n + 1, vector(W + 1, 0));
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= W; j++) {
// 当前物品重量大于背包容量,无法放入背包
if (items[i - 1].weight > j) {
dp[i][j] = dp[i - 1][j];
}
else {
// 考虑放入或不放入当前物品的两种情况,取最大值
dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - items[i - 1].weight] + items[i - 1].value);
}
}
}
return dp[n][W]; // 返回最优解
}
int main() {
int W = 10; // 背包容量
vector- items = { {2, 6}, {2, 10}, {3, 12} }; // 物品列表
int maxValue = knapsack(W, items); // 求解最优解
cout << "最大总价值为: " << maxValue << endl;
return 0;
}
一维数组思路:
在一维数组优化中,我们只需要创建一个长度为背包容量+1的一维数组,用于记录在不超过当前背包容量下的最优解。具体优化过程如下:
原始的二维dp数组定义为dp[n + 1][W + 1],其中dp[i][j]表示在前i个物品中选择不超过重量j的物品时的最优解。
将二维dp数组优化为一维数组dp[W + 1],其中dp[j]表示在不超过背包容量j的情况下的最优解。
优化后的代码示例:
#include
#include
using namespace std;
// 定义物品结构体,包含重量和价值
struct Item {
int weight;
int value;
};
int knapsack(int W, vector- & items) {
int n = items.size();
// 创建一维dp数组并初始化为0
vector
dp(W + 1, 0);
for (int i = 0; i < n; i++) {
for (int j = W; j >= items[i].weight; j--) {
// 考虑放入或不放入当前物品的两种情况,取最大值
dp[j] = max(dp[j], dp[j - items[i].weight] + items[i].value);
}
}
return dp[W]; // 返回最优解
}
int main() {
int W = 10; // 背包容量
vector- items = { {2, 6}, {2, 10}, {3, 12} }; // 物品列表
int maxValue = knapsack(W, items); // 求解最优解
cout << "最大总价值为: " << maxValue << endl;
return 0;
}
在上述代码中,我们使用一个长度为背包容量+1的一维数组dp[W + 1]来记录在不超过当前背包容量下的最优解。在计算时,我们从后往前遍历物品,并从后往前更新一维dp数组。这样可以确保在更新dp[j]时,所需的dp[j - items[i].weight]已经是前一轮的值,并且不会影响当前轮的计算结果。通过这种方式,可以实现将二维dp数组优化为一维数组的目的,并得到正确的最优解。
总结:
本文我们学习了01背包,其实我们可以发现动态规划题目还是有比较强的套路性的,我们把动态规划拆分成为了五部,我们只要按照这五步进行,实际上解决动态规划题目还是很简单的。
如果我的内容对你有帮助,请点赞,评论,收藏。创作不易,大家的支持就是我坚持下去的动力!
![]()