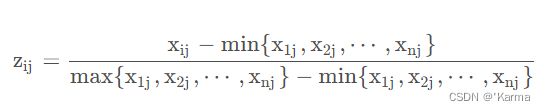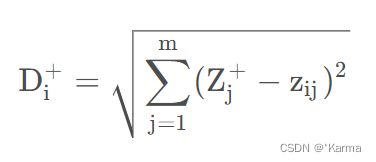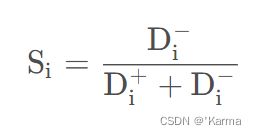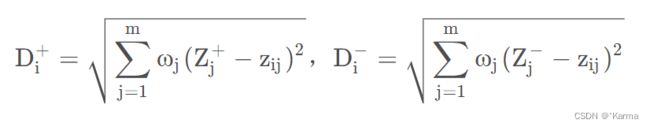Topsis 模型
评价方法大体上可分为两类,其主要区别在确定权重的方法上。一类是主观赋权法,多数采取综合咨询评分确定权重,如综合指数法、模糊综合评判法层次分析法、功效系数法等。另一类是客观赋权,根据各指标间相关关系或各指标值变异程度来确定权数,如主成分分析法、因子分析法、理想解排序法 (也称TOPSIS法,也称优劣解距离法)等。
一、理论步骤
1. 将原始矩阵正向化
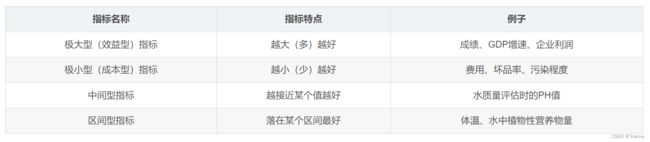
在生活中,常见的指标有四种:
在 TOPSIS 方法中,就是要将所有指标进行统一正向化,即统一转化为极大型指标。
① 极小型指标→极大型指标
直接用最大值max减去x;如果所有的元素均为正数,那么也可以使用:1/x
② 中间型指标→极大型指标
指标值既不要太大也不要太小,取某特定值最好(如水质量评估 PH 值):
以上都为线性变换。
③ 区间型指标→极大型指标
指标值落在某个区间内最好,例如人的体温在36°~37°这个区间比较好。
其中最佳区间为[a,b]
2. 正向化矩阵标准化
标准化的目的就是消除不同量纲的影响。
假设有n个要评价的对象,m个评价指标(已经正向化了)构成的正向化矩阵为X,那么对其标准化后的矩阵记为Z,Z的每一个元素:
如果zij中有负数,则需要这么处理:
matlab中标准化处理的函数:zscore(X)
3. 计算得分
定义最大值:
![]() 定义第i(i = 1,2,…,n)个评价对象与最大值的距离:
定义第i(i = 1,2,…,n)个评价对象与最大值的距离:
定义第i(i = 1,2,…,n)个评价对象与最小值的距离 :
那么,我们可以计算得出第 i( i = 1,2,…,n) 个评价对象未归一化的得分,得分越高越好:
二、代码
Topsis算法基本思想:基于归一化后的原始数据矩阵,采用余弦法找出有限方案中的最优方案和最劣方案(分别用最优向量和最劣向量表示),
然后分别计算各评价对象与最优方案和最劣方案间的距离,获得各评价对象与最优方案的相对接近程度,以此作为评价优劣的依据。
案例代码:x是需要评价的对象矩阵
clc,clear;
x=[
21584 76.7 7.3 1.01 78.3 97.5 2.0
24372 86.3 7.4 0.80 91.1 98.0 2.0
22041 81.8 7.3 0.62 91.1 97.3 3.2
21115 84.5 6.9 0.60 90.2 97.7 2.9
24633 90.3 6.9 0.25 95.5 97.9 3.6];%矩阵
[n,m]=size(x);
%将3,4,7的低优指标去倒数转化为高优指标并且把所有指标换成接近的大小
x(:,1)=x(:,1)/100;
x(:,3)=(1./x(:,3))*100;
x(:,4)=(1./x(:,4))*100;
x(:,7)=(1./x(:,7))*100; %主要是要将其转化为极大型指标
zh=zeros(1,m);
d1=zeros(1,n); %最小值矩阵
d2=zeros(1,n); %最大值矩阵
c=zeros(1,n); %接近程度
%标准化
for i=1:m
for j=1:n
zh(i)=zh(i)+x(j,i)^2;
end
end
for i=1:m
for j=1:n
x(j,i)=x(j,i)/sqrt( zh(i));
end
end
%计算距离
xx=min(x);
dd=max(x);
for i=1:n
for j=1:m
d1(i)=d1(i)+(x(i,j)-xx(j))^2;
end
d1(i)=sqrt(d1(i));
end
for i=1:n
for j=1:m
d2(i)=d2(i)+(x(i,j)-dd(j))^2;
end
d2(i)=sqrt(d2(i));
end
%计算接近程度
for i=1:n
c(i)=d1(i)/(d2(i)+d1(i));
end
[sf,ind]=sort(c,'descend'); %按降序排序
c,indind最后结果为5 2 1 4 3意思是最好的是第五个,其次是第二个……
三、模型优化
本道题目中默认了各项指标的权重相同,但在实际的评价中指标都是有各自的权重,因此应该用权重对公式进行修正,修正后的公式如下,ω 代表权重。
ω 可以由偏主观的层次分析法得出,也可由偏客观的熵权法得出,但是我建议使用综合主观与客观的权重,因为其更具有才更具说服力!