【数学】1、导论、数学归纳法与递归、分治

学习目标：

• 实用主义：为了解决工作日常的问题，而不是为了艰涩的数学理论，用多少学多少
• 思考本质：公式的推导并不重要，而思想、场景最重要，才能融会贯通。把握数学的工具属性，学习具体方法时先溯因再求果，勤于思考解决相同问题的不同方法，与解决不同问题的相同方法之间的联系与区别。
  • 特征向量计算的是系统的不动点，在数据降维中有举足轻重的作用，但如果熟悉电子通信的话你就会知道，对线性时不变系统的分析（也就是各种变换）都是基于特征向量展开的；
  • 在给定隐马尔可夫模型的观测序列时，可以利用维特比算法求解后验概率最大的状态序列，将这一方法应用在信道编码中，就是最经典的卷积码译码算法；
  • 在分类问题中，以类间方差最大化为标准可以推导出线性判别分析和决策树等模型，应用在图像处理中，类间方差最大化原理给出的就是图像分割中的 Otsu 方法。

学习方法：因为数学太难了，不建议直接啃书，先通过系统的课程（Coursera、公开课、专栏）提升广度，再在日常找机会应用得到正反馈、再了解数学的原理提升深度（可通过Coding The Matrix这本书学原理并编程实现）。

一、数学归纳法与递归

数学归纳法（Mathematical Induction）的结论是严格的，用来证明任意情形都是正确的，即第一个、第二个、第三个、知道所有情形。其步骤如下：

• 证明基本情况（通常是 n = 1 的时候）是否成立
• 假设 n = k−1 成立，再证明 n = k 也是成立的（k 为任意大于 1 的自然数）

1.1 数学归纳法的过程

举例场景如下：传说中的给64个格子的棋盘放麦粒，规则是第一格放一粒，第二格放两粒，以此类推，每一小格内都比前一小格多一倍的麦子，直至放满 64 个格子。求最终会放多少个麦粒。

通常我们可以试几个例子找规律，如下图，根据观察可大胆假设，前 n 个格子的麦粒总数是 $2^n-1$ 个：

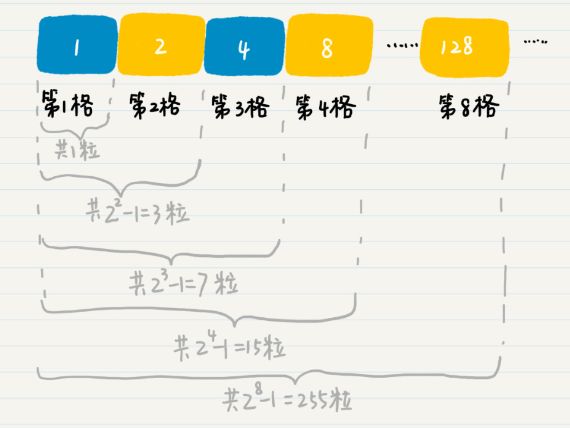
为了演示数学归纳法的推导过程，我们做两个猜想，并分别证明：

• 猜想1：第 n 个棋格放的麦粒数为 $2^{n-1}$，其证明如下：
  • 基本情况：已证明 n = 1 时，第一格麦粒数为 1，和 $2^1-1$ 相等。所以 k = 1 时猜想成立。
  • 假设第 k-1 格的麦粒数为 $2^{k-2}$，则因为第 k 格的麦粒数是 第 k-1 格的 2 倍，即 $2^{k-2}\ast 2=2^{k-1}$，所以猜想在 k = n-1 时成立。所以在 k = n 时也成立。
  • 所以猜想1成立
• 猜想2：前 n 个棋格放的麦粒数总和为 $2^n-1$，其证明如下（在猜想1已证明的前提下）：
  • 基本情况：已证明 n = 1 时，第一格麦粒数为 1，总麦粒数为1，和 $2^1-1$ 相等。所以 k = 1 时猜想成立。
  • 假设前 k-1 格麦粒总数为 $2^{k-1}-1$，根据已证实的猜想1得出第 k 格的麦粒数为 $2^{k-1}$，所以前 k 格的麦粒总数为 $(2^{k-1}-1)+(2^{k-1})=2\ast 2^{k-1}-1=2^k-1$。所以猜想在 k = n-1 时成立。所以在 k = n 时也成立。
  • 所以猜想2成立

数学归纳法中的“归纳”是指的从第一步正确，第二步正确，第三步正确，一直推导到最后一步是正确的。这就像多米诺骨牌，只要确保第一张牌倒下，而每张牌的倒下又能导致下一张牌的倒下，那么所有的骨牌都会倒下。

数学归纳法的特点：先找规律，再证明规律，不需要逐步的推演，节省了时间和资源。可以形象的理解：

• 递归：把计算交给计算机，是拿计算机的计算成本换人的时间
• 归纳：把计算交给人，是拿人的时间换计算机的计算成本

public static void main(String[] args) {
	int grid = 63;
	long start, end = 0;
	start = System.currentTimeMillis();
	System.out.println(String.format(" 舍罕王给了这么多粒：%d", Lesson3_1.getNumberOfWheat(grid)));
	end = System.currentTimeMillis();
	System.out.println(String.format(" 耗时 %d 毫秒 ", (end - start)));
	
	start = System.currentTimeMillis();
	System.out.println(String.format(" 舍罕王给了这么多粒：%d", (long)(Math.pow(2, grid)) - 1));
	end = System.currentTimeMillis();
	System.out.println(String.format(" 耗时 %d 毫秒 ", (end - start)));
}

// 这段代码运行的结果是：
// 舍罕王给了 9223372036854775807 粒，耗时 4 毫秒，用迭代消耗了计算机的 CPU 资源
// 舍罕王给了 9223372036854775806 粒，耗时 0 毫秒，因为已经得到了公式，所以没有用迭代消耗计算机的 CPU 资源，直接秒出结果

1.2 递归

1.2.1 本质就是数学归纳

如果把上例的数学归纳证明过程，转换成代码实现，则为如下：

• 第一步，如果 n 为 1，则判断麦粒总数是否为 $2^1-1=1$。同时，返回当前棋格的麦粒数，以及从第 1 格到当前棋格的麦粒总数。
• 第二步，如果 n 为 k−1 时成立，则判断 n 为 k 时是否也成立。此时的判断依赖于【前一格 k−1 的麦粒数】、第 1 格到 k−1 格的麦粒总数。即上一步所返回的两个值。

你应该看出来了，这两步分别对应了数学归纳法的两种情况。

• 在数学归纳法的第二种情况下，只能假设 n=k−1 时命题成立。
• 但在代码实现中，可将伪代码的第二步转为 函数的递归（嵌套）调用，在此递归中逐步返回【被调用的函数在 k−1 时命题是否成立】，直到被调用的函数回退到 n=1 的情况。

具体实现代码如下：

class Result {
    public long wheatNum = 0;  // 当前格的麦粒数
    public long wheatTotalNum = 0;  // 目前为止麦粒的总数
}

public class Lesson4_2 {
    public static void main(String[] args) {
        int grid = 63;
        Result result = new Result();
        System.out.println(Lesson4_2.prove(grid, result));
    }

    // @Description: 使用函数的递归（嵌套）调用，进行数学归纳法证明
    // @param k- 放到第几格，result- 保存当前格子的麦粒数和麦粒总数
    // @return boolean- 放到第 k 格时是否成立
    public static boolean prove(int k, Result result) {
        // 证明 n = 1 时，命题是否成立
        if (k == 1) {
            if ((Math.pow(2, 1) - 1) == 1) {
                result.wheatNum = 1;
                result.wheatTotalNum = 1;
                return true;
            } else return false;
        }
        // 如果 n = (k-1) 时命题成立，证明 n = k 时命题是否成立
        else {
            boolean proveOfPreviousOne = prove(k - 1, result);
            result.wheatNum *= 2;
            result.wheatTotalNum += result.wheatNum;
            boolean proveOfCurrentOne = false;
            if (result.wheatTotalNum == (Math.pow(2, k) - 1)) proveOfCurrentOne = true;

            return proveOfPreviousOne && proveOfCurrentOne
        }
    }
}

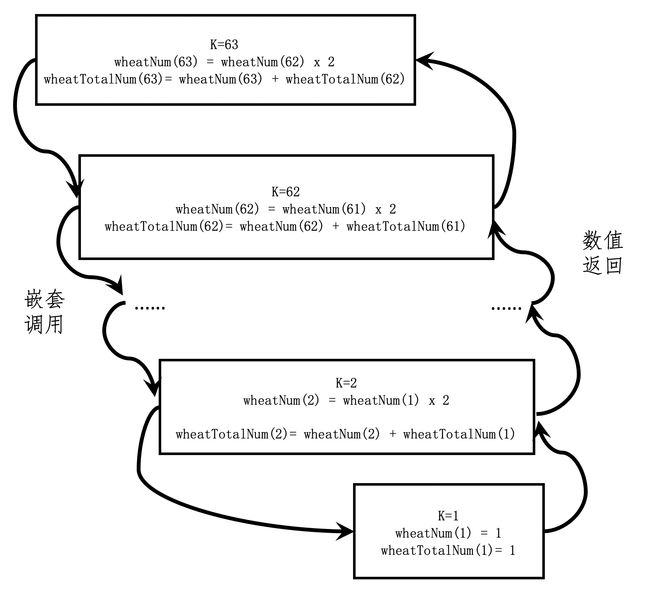
上述代码的调用链如下图所示：函数从 k=63 开始调用，然后调用 k−1，也就是 62，一直到 k=1 的时候，嵌套调用结束，k=1 的函数体开始返回值给 k=2 的函数体，一直到 k=63 的函数体。从 k=63,62,…,2,1 的嵌套调用过程，其实就是体现了数学归纳法的核心思想，我把它称为逆向递推。而从 k=1,2,…,62,63 的值返回过程，和上一篇中基于循环的迭代是一致的，我把它称为正向递推。

所以，递归代码和数学归纳法的逻辑是一致的。实操时只需保证用数学归纳法的两个证明步骤写出递归代码，则递归的逻辑就在宏观上一定是对的，而不需要纠结微观的递归函数是如何嵌套和返回的。

编程时注意：递归需要用变量将 k-1 的状态传递到 k，可通过传参+返回值或类内的公共变量实现。

1.2.2 递归的场景

既然递归的函数值返回过程和基于循环的迭代法一致，我们直接用迭代法不就好了，为什么还要用递归的数学思想和编程方法呢？这是因为，在某些场景下，递归的解法比基于循环的迭代法更容易实现。原因如下两点？

• 第一，递归的核心思想和数学归纳法类似，并更具有广泛性。这两者的类似之处体现在：将当前的问题化解为两部分：一个当前所采取的步骤和另一个更简单的问题。
  • 一个当前所采取的步骤：这种步骤可能是进行一次运算（例如每个棋格里的麦粒数是前一格的两倍），或者做一个选择（例如选择不同面额的纸币），或者是不同类型操作的结合（例如今天讲的赏金的案例）等等。
  • 另一个更简单的问题：经过上述步骤之后，问题就会变得更加简单一点。这里“简单一点”，指运算的结果离目标值更近（例如赏金的总额），或者是完成了更多的选择（例如纸币的选择）。而“更简单的问题”，又可以通过嵌套调用，进一步简化和求解，直至达到结束条件。
  • 我们只需要保证递归编程能够体现这种将复杂问题逐步简化的思想，那么它就能帮助我们解决很多类似的问题。
• 第二，递归会使用计算机的函数嵌套调用。而函数的调用本身，就可以保存很多中间状态和变量值，因此极大的方便了编程的处理。
  • 正是如此，递归在计算机编程领域中有着广泛的应用，而不仅仅局限在求和等运算操作上。

我们继续来看舍罕王赏麦的故事：如何在限定总和的情况下，求所有可能的加和方式？

舍罕王和他的宰相西萨·班·达依尔现在来到了当代。这次国王学乖了，他对宰相说：“这次我不用麦子奖赏你了，我直接给你货币。另外，我也不用棋盘了，我直接给你一个固定数额的奖赏。”

宰相思考了一下，回答道：“没问题，陛下，就按照您的意愿。不过，我有个小小的要求。那就是您能否列出所有可能的奖赏方式，让我自己来选呢？假设有四种面额的钱币，1 元、2 元、5 元和 10 元，而您一共给我 10 元，那您可以奖赏我 1 张 10 元，或者 10 张 1 元，或者 5 张 1 元外加 1 张 5 元等等。如果考虑每次奖赏的金额和先后顺序，那么最终一共有多少种不同的奖赏方式呢？”

让我们再次帮国王想想，如何解决这个难题吧。这个问题和之前的棋盘上放麦粒有所不同，它并不是要求你给出最终的总数，而是在限定总和的情况下，求所有可能的加和方式。你可能会想，虽然问题不一样，但是求和的重复性操作仍然是一样的，因此是否可以使用迭代法？好，让我们用迭代法来试一下。

我还是使用迭代法中的术语，考虑 k=1,2,3,…,n 的情况。在第一步，也就是当 n=1 的时候，我们可以取四种面额中的任何一种，那么当前的奖赏就是 1 元、2 元、5 元和 10 元。当 n=2 的时候，奖赏的总和就有很多可能性了。如果第一次奖赏了 1 元，那么第二次有可能取 1、2、5 元三种面额（如果取 10，总数超过了 10 元，因此不可能）。

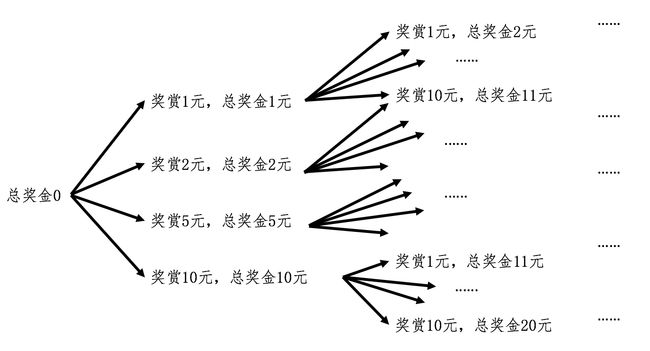
所以，在第一次奖赏 1 元，第二次奖赏 1 元后，总和为 2 元；第一次奖赏 1 元，第二次奖赏 2 元后，总和为 3 元；第一次奖赏 1 元，第二次奖赏 5 元后，总和为 6 元。好吧，这还没有考虑第一次奖赏 2 元和 5 元的情况。我来画个图，从图中你就能发现这种可能的情况在快速地“膨胀”。

你应该能看到，虽然迭代法的思想是可行的，但是如果用循环来实现，恐怕要保存好多中间状态及其对应的变量。说到这里，你是不是很容易就想到计算编程常用的函数递归？

在递归中，每次嵌套调用都会让函数体生成自己的局部变量，正好可以用来保存不同状态下的数值，为我们省去了大量中间变量的操作，极大地方便了设计和编程。

不过，这里又有新的问题了。之前用递归模拟数学归纳法还是非常直观的。可是，这里不是要计算一个最终的数值，而是要列举出所有的可能性。那应该如何使用递归来解决呢？上一节，我只是用递归编程体现了数学归纳法的思想，但是如果我们把这个思想泛化一下，那么递归就会有更多、更广阔的应用场景。

1.2.2.1 编程实现数学归纳

首先，我们来看，如何将数学归纳法的思想泛化成更一般的情况？数学归纳法考虑了两种情况：

• 初始状态，也就是 n=1 的时候，命题是否成立；
• 如果 n=k-1 的时候，命题成立。那么只要证明 n=k 的时候，命题也成立。其中 k 为大于 1 的自然数。

将上述两点顺序更换一下，再抽象化一下，我写出了这样的递推关系：

• 假设 n=k-1 的时候，问题已经解决（或者已经找到解）。那么只要求解 n=k 的时候，问题如何解决（或者解是多少）；
• 初始状态，就是 n=1 的时候，问题如何解决（或者解是多少）。

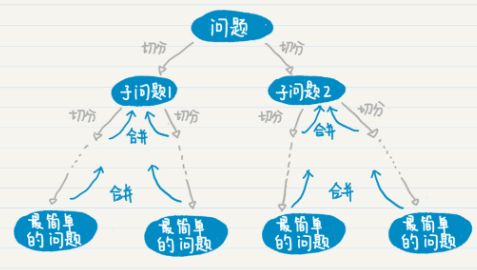
这种思想就是将复杂的问题，每次都解决一点点，并将剩下的任务转化成为更简单的问题等待下次求解，如此反复，直到最简单的形式。回到开头的例子，我们再将这种思想具体化。

• 假设 n=k-1 的时候，我们已经知道如何去求所有奖赏的组合。那么只要求解 n=k 的时候，会有哪些金额的选择，以及每种选择后还剩下多少奖金需要支付就可以了。
• 初始状态，就是 n=1 的时候，会有多少种奖赏。

import java.util.ArrayList;
public class Main {
	public static long[] rewards = {1, 2, 5, 10};	// 四种面额的纸币
	public static void main(String[] args) {
		int totalReward = 10;
		get(totalReward, new ArrayList<Long>());
	}
	/**
	 * @Description:	使用函数的递归（嵌套）调用，找出所有可能的奖赏组合
	 * @param totalReward- 奖赏总金额，result- 保存当前的解
	 * @return void
	 */
	public static void get(long totalReward, ArrayList<Long> result) {
		// 当 totalReward = 0 时，证明它是满足条件的解，结束嵌套调用，输出解
		if (totalReward == 0) {
			System.out.println(result);
			return;
		}
		// 当 totalReward < 0 时，证明它不是满足条件的解，不输出
		else if (totalReward < 0) {
			return;
		} else {
			for (int i = 0; i < rewards.length; i++) {
				ArrayList<Long> newResult = (ArrayList<Long>)(result.clone());	// 由于有 4 种情况，需要 clone 当前的解并传入被调用的函数
				newResult.add(rewards[i]);						// 记录当前的选择，解决一点问题
				get(totalReward - rewards[i], newResult);		// 剩下的问题，留给嵌套调用去解决
			}
		}
	}
}

// 输出如下: 共129种可能
[1, 1, 1, 1, 1, 1, 1, 1, 1, 1] // 分 10 次奖赏，每次 1 元
[1, 1, 1, 1, 1, 1, 1, 1, 2] // 分 9 次奖赏，最后一次是 2 元
[1, 1, 1, 1, 1, 1, 1, 2, 1]
[1, 1, 1, 1, 1, 1, 2, 1, 1]
[1, 1, 1, 1, 1, 1, 2, 2]
...
[5, 5]
[10]

// 代码有如下注意：
// 1. 由于一共只有 4 种金额的纸币，所以无论是 n=1 的时候还是 n=k 的时候，我们只需要关心这 4 种金额对组合产生的影响，而中间状态和变量的记录和跟踪这些繁琐的事情都由函数的递归调用负责。
// 2. 这个案例的限制条件不再是 64 个棋格，而是奖赏的总金额，因此判断嵌套调用是否结束的条件其实不是次数 k，而是总金额。这个金额确保了递归不会陷入死循环。
// 3. 我这里从奖赏的总金额开始，每次嵌套调用的时候减去一张纸币的金额，直到所剩的金额为 0 或者少于 0，然后结束嵌套调用，开始返回结果值。当然，你也可以反向操作，从金额 0 开始，每次嵌套调用的时候增加一张纸币的金额，直到累计的金额达到或超过总金额。

练习：一个整数可以被分解为多个整数的乘积，例如，6 可以分解为 2x3。请使用递归编程的方法，为给定的整数 n，找到所有可能的分解（1 在解中最多只能出现 1 次）。例如，输入 8，输出是可以是 1x8, 8x1, 2x4, 4x2, 1x2x2x2, 1x2x4, ……

package main
import "fmt"

func main() {
	f(6, []int{})
}

func f(total int, ans []int) {
	if total == 1 { // 递归终止条件
		if !has(ans, 1) {ans = append(ans, 1)}
		fmt.Print(ans) // 递归结束, 打印最终结果数组
		return
	}
	for i := 1; i <= total; i++ {
		if i == 1 && has(ans, 1) {continue} // 防止向ans中重复写入1
		if total%i == 0 {
			f(total/i, append(ans, i)) // 注意递归时需防止不同分支的写操作互相干扰。而此题因为是串行的, 故此处没有用copy()拷贝原ans数组
		}
	}
}

func has(arr []int, v int) bool {
	for _, a := range arr {
		if a == v {return true}
	}
	return false
}

// code result:
[1 2 3][1 3 2][1 6][2 1 3][2 3 1][3 1 2][3 2 1][6 1]

1.2.2.2 归并排序的分治思想

归并排序算法的核心就是“归并”，也就是把两个有序的数列合并起来，形成一个更大的有序数列。

假设我们需要按照从小到大的顺序，合并两个有序数列 A 和 B。这里我们需要开辟一个新的存储空间 C，用于保存合并后的结果。

我们首先比较两个数列的第一个数，如果 A 数列的第一个数小于 B 数列的第一个数，那么就先取出 A 数列的第一个数放入 C，并把这个数从 A 数列里删除。如果是 B 的第一个数更小，那么就先取出 B 数列的第一个数放入 C，并把它从 B 数列里删除。

以此类推，直到 A 和 B 里所有的数都被取出来并放入 C。如果到某一步，A 或 B 数列为空，那直接将另一个数列的数据依次取出放入 C 就可以了。这种操作，可以保证两个有序的数列 A 和 B 合并到 C 之后，C 数列仍然是有序的。

例如下图为合并有序数组{1, 2, 5, 8}和{3, 4, 6}的过程：

为了保证得到有序的 C 数列，我们必须保证参与合并的 A 和 B 也是有序的。可是，等待排序的数组一开始都是乱序的，如果无法保证这点，那归并又有什么意义呢？

还记得上一篇说的递归吗？这里我们就可以利用递归的思想，把问题不断简化，也就是把数列不断简化，一直简化到只剩 1 个数。1 个数本身就是有序的，对吧？

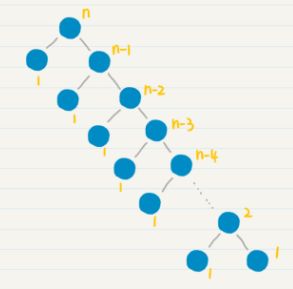
好了，现在剩下的疑惑就是，每一次如何简化问题呢？最简单的想法是，我们把将长度为 n 的数列，每次简化为长度为 n-1 的数列，直至长度为 1。不过，这样的处理没有并行性，要进行 n-1 次的归并操作，效率就会很低。

所以，我们可以在归并排序中引入了【分而治之（Divide and Conquer）】的思想。分而治之，我们通常简称为分治。它的思想是，将一个复杂的问题，分解成两个甚至多个规模相同或类似的子问题，然后对这些子问题再进一步细分，直到最后的子问题变得很简单，很容易就能被求解出来，这样这个复杂的问题就求解出来了。

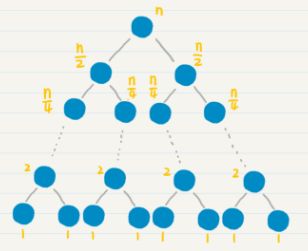
归并排序通过分治的思想，把长度为 n 的数列，每次简化为两个长度为 n/2 的数列。这更有利于计算机的并行处理，只需要 $lo{g}_{2}n$ 次归并。

我们把归并和分治的思想结合起来，这其实就是归并排序算法。这种算法每次把数列进行二等分，直到唯一的数字，也就是最基本的有序数列。然后从这些最基本的有序数列开始，两两合并有序的数列，直到所有的数字都参与了归并排序。

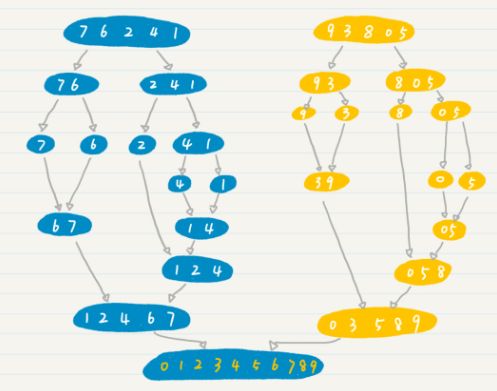
我用一个包含 0～9 这 10 个数字的数组，给你详细讲解一下归并排序的过程。
假设初始的数组为{7, 6, 2, 4, 1, 9, 3, 8, 0, 5}，我们要对它进行从小到大的排序。
第一次分解后，变成两个数组{7, 6, 2, 4, 1}和{9, 3, 8, 0, 5}。
然后，我们将{7, 6, 2, 4, 1}分解为{7, 6}和{2, 4, 1}，将{9, 3, 8, 0, 5}分解为{9, 3}和{8, 0, 5}。
如果细分后的组仍然多于一个数字，我们就重复上述分解的步骤，直到每个组只包含一个数字。到这里，这些其实都是递归的嵌套调用过程。
然后，我们要开始进行合并了。我们可以将{4, 1}分解为{4}和{1}。现在无法再细分了，我们开始【合并】。在合并的过程中进行【排序】，所以合并的结果为{1,4}。合并后的结果将【返回】当前函数的调用者，这就是函数返回的过程。
重复上述合并的过程，直到完成整个数组的排序，得到{0, 1, 2, 3, 4, 5, 6, 7, 8, 9}。

如下图所示：

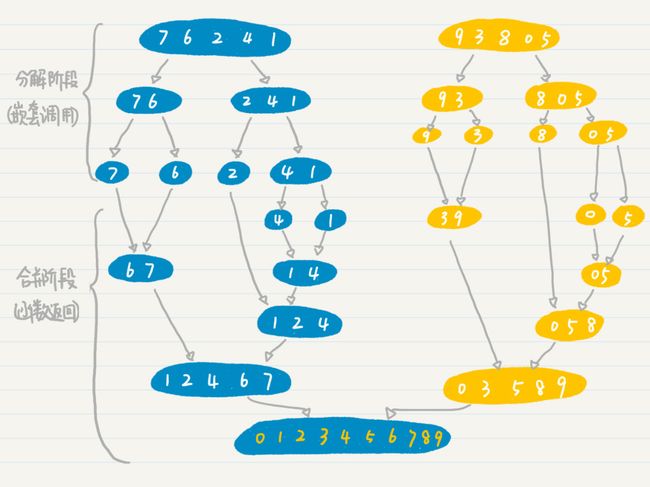
归并排序算法用分治的思想把数列不断地简化，直到每个数列仅剩下一个单独的数，然后再使用归并逐步合并有序的数列，从而达到将整个数列进行排序的目的。而这个归并排序，正好可以使用递归的方式来实现。为什么这么说？首先，我们看下图，分治的过程是不是和递归的过程一致呢？

分治的过程可以通过递归来表达，因此，归并排序最直观的实现方式就是递归。所以，我们从递归的步骤出发，来看归并排序如何实现。

我们假设 n=k-1 的时候，我们已经对较小的两组数进行了排序。那我们只要在 n=k 的时候，将这两组数合并起来，并且保证合并后的数组仍然是有序的就行了。

所以，在递归的每次嵌套调用中，代码都将一组数分解成更小的两组，然后将这两个小组的排序交给下一次的嵌套调用。而本次调用只需要关心，如何将排好序的两个小组进行合并。

在初始状态，也就是 n=1 的时候，对于排序的案例而言，只包含单个数字的分组。由于分组里只有一个数字，所以它已经是排好序的了，之后就可以开始递归调用的返回阶段。如下图：

代码实现如下：

import java.util.Arrays;
public class Lesson6_1 {
    // @Description:	使用函数的递归（嵌套）调用，实现归并排序（从小到大）
    // @param to_sort- 等待排序的数组
    // @return int[]- 排序后的数组
	public static int[] merge_sort(int[] to_sort) {
		if (to_sort == null) return new int[0];
		
		// 如果分解到只剩一个数，返回该数
		if (to_sort.length == 1) return to_sort;
		
		// 将数组分解成左右两半
		int mid = to_sort.length / 2;
		int[] left = Arrays.copyOfRange(to_sort, 0, mid);
		int[] right = Arrays.copyOfRange(to_sort, mid, to_sort.length);
		
		// 嵌套调用，对两半分别进行排序
		left = merge_sort(left);
		right = merge_sort(right);
		
		// 合并排序后的两半
		int[] merged = merge(left, right);
		return merged;
	}
}

其中合并过程代码如下：

public static int[]merge(int[]a, int[]b){
    if(a==null) a=new int[0];
    if(b==null) b=new int[0];

    int[]merged_one=new int[a.length+b.length];

    int mi=0, ai=0, bi=0;

    // 轮流从两个数组中取出较小的值，放入合并后的数组中
    while(ai < a.length && bi < b.length){
        if (a[ai] <= b[bi]){
            merged_one[mi] = a[ai];
            ai++;
        } else {
            merged_one[mi] = b[bi];
            bi++;
        }
        mi++;
    }

    // 将某个数组内剩余的数字放入合并后的数组中
    if (ai < a.length){
        for(int i = ai;i < a.length;i++){
            merged_one[mi] = a[i];
            mi++;
        }
    } else {
        for(int i = bi; i < b.length; i++){
            merged_one[mi] = b[i];
            mi++;
        }
    }
    return merged_one;
}

调用过程如下：

public static void main(String[] args) {
  int[] to_sort = {3434, 3356, 67, 12334, 878667, 387};
  int[] sorted = Lesson6_1.merge_sort(to_sort);
  
  for (int i = 0; i < sorted.length; i++) {
  	System.out.println(sorted[i]);
  }
}

1.2.2.3 分布式系统的分治思想

当需要排序的数组很大（比如达到 1024GB 的时候），我们没法把这些数据都塞入一台普通机器的内存里。该怎么办呢？有一个办法，我们可以把这个超级大的数据集，分解为多个更小的数据集（比如 16GB 或者更小），然后分配到多台机器，让它们并行地处理。

等所有机器处理完后，中央服务器再进行结果的合并。由于多个小任务间不会相互干扰，可以同时处理，这样会大大增加处理的速度，减少等待时间。

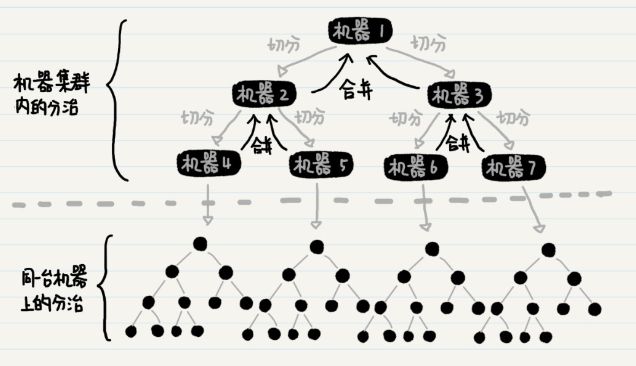
在单台机器上实现归并排序的时候，我们只需要在递归函数内，实现数据分组以及合并就行了。而在多个机器之间分配数据的时候，递归函数内除了分组及合并，还要负责把数据分发到某台机器上。

上图中的父结点，例如机器 1、2、3，它们都没有被分配排序的工作，只是在子结点的排序完成后进行有序数组的合并，因此集群的性能没有得到充分利用。那么，另一种可能的数据切分方式是，每台机器拿出一半的数据给另一台机器处理，而自己来完成剩下一半的数据。

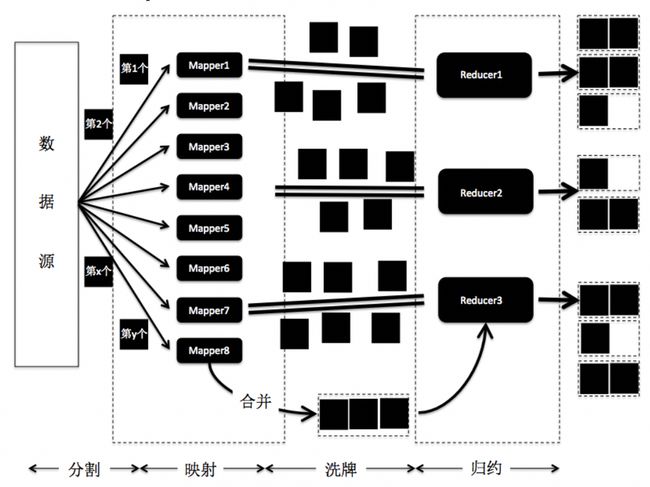
如果分治的时候，只进行一次问题切分，那么上述层级型的分布式架构就可以转化为类似 MapReduce 的架构。我画出了 MapReduce 的主要步骤，其如下步骤体现分治思想：

1. 数据分割和映射：分割是指将数据源进行切分，并将分片发送到 Mapper 上。映射是指 Mapper 根据应用的需求，将内容按照键 - 值的匹配，存储到哈希结构中。这两个步骤将大的数据集合切分为更小的数据集，降低了每台机器节点的负载，因此和分治中的问题分解类似。不过，MapReduce 采用了哈希映射来分配数据，而普通的分治或递归不一定需要。
2. 归约：归约是指接受到的一组键值配对，如果是键内容相同的配对，就将它们的值归并。这和本机的递归调用后返回结果的过程类似。不过，由于哈希映射的关系，MapReduce 还需要洗牌的步骤，也就是将键 - 值的配对不断地发给对应的 Reducer 进行归约。普通的分治或递归不一定需要洗牌的步骤。
3. 合并：为了提升洗牌阶段的效率，可以选择减少发送到归约阶段的键 - 值配对。具体做法是在数据映射和洗牌之间，加入合并的过程，在每个 Mapper 节点上先进行一次本地的归约。然后只将合并的结果发送到洗牌和归约阶段。这和本机的递归调用后返回结果的过程类似。
   

上述介绍的是最经典的2路归并排序算法，时间复杂度是O(NlogN)。如果将数组分解成更多组（假设分成K组），是K路归并排序算法，当然是可以的，比如K=3时，是3路归并排序，依次类推。3路归并排序是经典的归并排序（路归并排序）的变体，通过递归树方法计算等式T(n)= 3T(n/3)+ O(n)可以得到3路归并排序的时间复杂度为O(NlogN)，其中logN以3为底（不方便打出，只能这样描述）。