【计算机视觉】关于图像处理的一些基本操作
目录
-
- 图像平滑滤波处理
-
- 均值滤波
-
- 计算过程
- python实现
- 高斯滤波
-
- 计算过程
- python实现
- 中值滤波
-
- 计算过程
- python实现
- 图像的边缘检测
-
- Robert算子
-
- 计算过程
- python实现
- 图像处理
-
- 腐蚀算子
-
- 计算过程
- python实现
- Hog(梯度方向直方图)特征
-
- 计算流程:
- Hog的特征维度计算公式
- python实现
- 普通卷积/池化的输出尺寸与感受野计算公式
-
- 普通卷积的输出尺寸
- 池化操作的输出尺寸
- 卷积的感受野
- 不同卷积的计算量与参数量
-
- 常规卷积的计算量与参数量
- 分组卷积
- 深度可分解卷积的计算量与参数量
- Batchnorm层的操作
-
- Batchnorm层中可学习的参数
图像平滑滤波处理
图像平滑是指受传感器和大气等因素的影响,遥感图像上会出现某些亮度变化过大的区域,或出现一些亮点(也称噪声)。这种为了抑制噪声,使图像亮度趋于平缓的处理方法就是图像平滑。图像平滑实际上是低通滤波,平滑过程会导致图像边缘模糊化。
均值滤波
线性滤波,针对整个图像矩阵操作。
- 特点:窗口大小越大,去噪效果越好,当然花费的计算时间也会越长,同时让图像失真越严重。在实际处理中,要在失真和去噪效果之间取得平衡,选取合适大小的窗口大小。
- 【优点】算法简单,不需要复杂的图像处理技术,也不需要花费大量的时间和空间。而且它可以有效地消除噪声,改善图像质量。
- 【缺点】均值滤波本身存在着固有的缺陷,即它不能很好地保护图像细节,在图像去噪的同时也破坏了图像的细节部分,从而使图像变得模糊,不能很好地去除噪声点。
- 【适用范围】椒盐噪声
- 【不适合范围】低照度、强噪声图像
计算过程
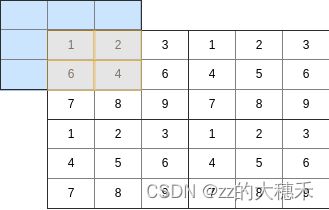
对于一个给定的窗口大小,计算窗口内的数值的平均值,然后使用中间值作为窗口中心值。例如输入3,表示用一个 3 × 3 3 \times 3 3×3的窗口去重新计算给出图像矩阵的像素值。【注意:在边缘的那些像素(不能成为 3 × 3 3 \times 3 3×3的窗口的中心点)则计算部分有效的像素】
如下图所示,对于第一行第一列的像素点1,依然以它为中心,取橙色区域的均值作为它的新值。
python实现
import cv2
import numpy as np
x = np.array([[1, 3, 2, 4, 6, 5, 7]])
# 对图像进行均值滤波,指定核大小为5x5
result1 = cv2.blur(x, (3, 3))
print(result1)
高斯滤波
线性滤波,针对整个图像矩阵操作。
- 【特点】
- 在高斯滤波中,核的宽度和高度可以不相同,但是它们都必须是奇数。
- 对应均值滤波来说,其邻域内每个像素的权重是相等的。而在高斯滤波中,会将中心点的权重值加大,远离中心点的权重值减小,在此基础上计算邻域内各个像素值不同权重的和。
- 高斯核可看作卷积核,同样为二维滤波器矩阵,不同的是高斯核在普通卷积核的基础上进行了加权处理(权重矩阵由高斯函数计算得到)。
- 【优点】去除图像中噪音和细节信息的同时,保留图像的主要特点(例如图像的轮廓和边缘);可以通过调整高斯核的大小和标准差控制高斯滤波器的模糊程度。
- 【缺点】计算复杂度高,因为高斯滤波器需要进行卷积运算。
- 【适用范围】消除高斯噪声
计算过程
高斯滤波通常有两种方法实现,一种是离散化窗口滑窗卷积;第二种是通过傅里叶变换。以下是用离散化窗口滑窗卷积实现的高斯滤波。
常用的高斯模板如下: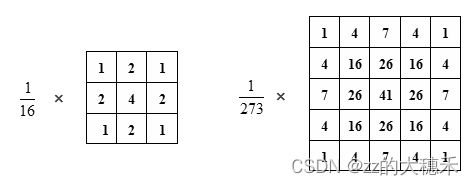 以上参数是通过高斯函数计算得到,参照关于高斯滤波的一些理解。
以上参数是通过高斯函数计算得到,参照关于高斯滤波的一些理解。
具体操作是:用一个模板(或称卷积、掩模)扫描图像中的每一个像素,用模板确定的邻域内像素的加权平均灰度值去替代模板中心像素点的值。
具体参考高斯滤波(Gauss filtering)
python实现
import numpy as np
import cv2
x = np.array([[1, 3, 2, 4, 6, 5, 7]])
# (3,3)为滤波器的大小;1.3为滤波器的标准差,如果标准差这个参数设置为0,则程序会根据滤波器大小自动计算得到标准差。
pic = cv2.GaussianBlur(x, (1, 3), 1.3, 1.3)
print(pic)
中值滤波
非线性滤波,针对图像矩阵中成为窗口中间点的像素点。
- 【优点】它在平滑脉冲噪声方面非常有效,同时它可以保护图像尖锐的边缘,选择适当的点来替代污染点的值,所以处理效果好。
- 【缺点】容易导致图像的不连续性;相比与均值滤波,处理大尺寸图像速度慢,因为有排序操作。
- 【适用范围】消除椒盐噪声、加性高斯噪音等随机噪声
- 【不适合范围】不适合于连续性噪声。
计算过程
对于一个给定的窗口大小,将窗口内的数值排序,然后使用中间值作为窗口中心值。 例如输入3,表示用一个 3 × 3 3 \times 3 3×3的窗口去重新计算给出图像矩阵的像素值。【注意:参与滤波的像素是窗口的中心点,在边缘的那些像素(不能成为 3 × 3 3 \times 3 3×3的窗口的中心点)是不会进行计算的。】
下图为对 6 × 6 6\times 6 6×6图像矩阵进行中值滤波,蓝色是滑动的窗口,红色的值是滤波后的值。如图所示,边缘像素不会参与计算,真正参与计算的像素值是窗口的中心点。

python实现
import scipy.signal as ss
x = [1, 3, 2, 4, 6, 5, 7]
pic = ss.medfilt(x, 3)
print(pic)
图像的边缘检测
图像边缘一般指图像的灰度变化率最大的位置。成因主要如下:
-
图像灰度在表面法向变化不连续;
-
图像中物体在空间上的深度不一致;
-
在光滑的表面上颜色不一致;
-
图像中物体的光影
边缘检测指的是从图像中检测边缘点和边缘段,并且描述边缘方向的过程。
Robert算子
一阶微分算子,是一种斜向偏差分的梯度计算方法,梯度的大小代表边缘的强度,梯度的方向与边缘的走向垂直(正交)。
- 【优点】计算简单,边缘定位准确。
- 【缺点】对噪声及其敏感
- 【适用范围】擅长处理具有陡峭(边缘明显)的低噪声的图像
- -【不适用范围】噪声多的图像
计算过程
x方向的Robert算子梯度窗口:
G x = [ 1 0 0 − 1 ] G_x=\begin{bmatrix}1 &0\\ 0&-1 \end{bmatrix} Gx=[100−1]
y方向的Robert算子梯度窗口:
G x = [ 0 1 − 1 0 ] G_x=\begin{bmatrix}0 &1\\ -1&0 \end{bmatrix} Gx=[0−110]
图片矩阵中像素点的梯度和(可以是两者绝对值最大值或平方根):
G = ∣ G x ∣ + ∣ G y ∣ G=|G_x|+|G_y| G=∣Gx∣+∣Gy∣
得到以上两个梯度窗口及其加法方式后,应用于图像矩阵中,注意,图像矩阵最后一行和最后第一列不参与计算,直接置为0。因为以上的计算思想相当于计算 ( x 1 2 , y 1 2 ) (x_\frac{1}{2},y_\frac{1}{2}) (x21,y21)的梯度。
python实现
import numpy as np
def Roberts(img_arr,r_x, r_y):
w, h = img_arr.shape
res = np.zeros((w, h)) # 取一个和原图一样大小的图片,并在里面填充0
for x in range(w-2):
for y in range(h-2):
sub = img_arr[x:x + 2, y:y + 2]
roberts_x = np.array(r_x)
roberts_y = np.array(r_y)
var_x =sum(sum(sub * roberts_x))#矩阵相乘,查看公式,我们要得到是一个值,所以对它进行两次相加
var_y = sum(sum(sub * roberts_y))
var = abs(var_x) + abs(var_y)
res[x][y] = var#把var值放在x行y列位置上
return res
pic_arr = np.array([[0, 0, 0, 0], [0, 10, 10, 0], [0, 10, 10, 0], [0, 0, 0, 0]])
r_x = [[1, 0], [0, -1]]
r_y = [[1, 1], [-1, 0]]
pic = Roberts(pic_arr, r_x, r_y)
print(pic)
图像处理
腐蚀算子
针对图像矩阵的每一个像素计算。
- 特点:图像的腐蚀是相较于高亮部分而言,对应的二值化图像就是对白色区域而言,腐蚀通俗来讲就是对将白色部分在原来的形状上缩小,对黑色部分扩大,腐蚀和膨胀操作相反。
- 【适用范围】
-
消除噪声
-
分割图像和连接图像
-
求局部最大值和局部最小值(对图像进行数学卷积运算)
-
求图像的梯度
-
计算过程
输入一个图片矩阵(0/1矩阵),和一个模板矩阵(也称为卷积核,0/1取值)。将该模板矩阵中以标记为“中心”的像素点为基准在图片矩阵中逐像素平移。针对【模板矩阵中值为1的像素点】与【图片矩阵中对应大小像素点】取“与”,将结果的最小值赋值给当前的像素。只有当图片矩阵中1的形状与模板矩阵中取值为1的形状相同的部分才会保留下来。
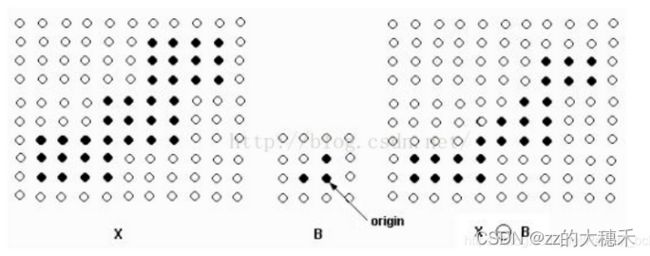
例如下图:B为模板矩阵(B中‘origin’表示中心点),X为图片矩阵,X-B表示腐蚀后的结果。该结果可以视为,B中黑色部分在X中的黑色部分取“与”操作。
python实现
Hog(梯度方向直方图)特征
计算流程:
-
图像预处理:将图像转换为灰度图像,并对像素值进行归一化。如果图像中出现了强反射等亮度不稳定的情况,需要进行光照归一化等处理。
-
计算梯度和方向直方图:对图像进行卷积操作,得到梯度大小和方向,然后将图像分成若干个小块(例如 8 × 8 8\times8 8×8 的小块),对每个小块内的梯度方向进行统计,得到该小块内的梯度方向直方图。
-
归一化:对每个小块内的梯度方向直方图进行归一化,以避免光照和阴影等因素的影响。
-
拼接:将所有小块的归一化直方图拼接成一个大向量,称为 HOG 特征向量。
Hog的特征维度计算公式
例子:
给定分辨率 H × W = 100 × 100 H\times W = 100 \times 100 H×W=100×100的图像,已知cell包含像素大小是 c e l l s i z e = 8 × 8 cell_{size}=8\times8 cellsize=8×8,每个cell的直方图数 b i n s = 9 bins=9 bins=9,每 4 × 4 4\times4 4×4个cell组成一个 b l o c k block block,扫描步长为 8 8 8像素。
则对于该图的Hog特征的维度计算如下:
- b l o c k s i z e = ( 4 × 8 ) × ( 4 × 8 ) = 32 × 32 block_{size}= (4 \times 8)\times(4 \times 8)=32\times32 blocksize=(4×8)×(4×8)=32×32
- 默认 b l o c k s t r i d e = c e l l s i z e = 8 block_{stride} =cell_{size}=8 blockstride=cellsize=8,
- b l o c k H / W = ( H ( W ) − b l o c k s i z e ) b l o c k s t r i d e + 1 = 9 block_{H/W}=\frac{(H(W)-block_{size})}{block_{stride}}+1=9 blockH/W=blockstride(H(W)−blocksize)+1=9
- b l o c k n u m = 9 × 9 = 81 block_{num} =9\times9=81 blocknum=9×9=81
- 特征维度= b i n s × b l o c k n u m × 每个 b l o c k 包含 c e l l 数 = 9 × 81 × 16 = 11664 bins\times block_{num}\times 每个block包含cell数=9\times 81\times 16=11664 bins×blocknum×每个block包含cell数=9×81×16=11664
根据上述计算方式,可以得到一个 N N N 维的 HOG 特征向量。
python实现
import cv2
import numpy as np
gray_pic = np.ones(shape=(32, 64), dtype=np.uint8)
# 为HOG描述符指定参数
# 像素大小(以像素为单位)(宽度,高度)。 它必须小于检测窗口的大小,
# 并且必须进行选择,以使生成的块大小小于检测窗口的大小。
cell_size = (4, 4)
# 每个方向(x,y)上每个块的单元数。 必须选择为使结果
# 块大小小于检测窗口
num_cells_per_block = (2, 2)
# 块大小(以像素为单位)(宽度,高度)。必须是“单元格大小”的整数倍。
# 块大小必须小于检测窗口。
block_size = (num_cells_per_block[0] * cell_size[0],
num_cells_per_block[1] * cell_size[1])
# 计算在x和y方向上适合我们图像的像素数
x_cells = gray_pic.shape[1] // cell_size[0]
y_cells = gray_pic.shape[0] // cell_size[1]
# 块之间的水平距离,以像元大小为单位。 必须为整数,并且必须
# 将其设置为(x_cells-num_cells_per_block [0])/ h_stride =整数。
h_stride = 1
# 块之间的垂直距离,以像元大小为单位。 必须为整数,并且必须
# 将其设置为 (y_cells - num_cells_per_block[1]) / v_stride = integer.
v_stride = 1
# 块跨距(以像素为单位)(水平,垂直)。 必须是像素大小的整数倍。
block_stride = (cell_size[0] * h_stride, cell_size[1] * v_stride)
# 梯度定向箱的数量
num_bins = 9
# 指定检测窗口(感兴趣区域)的大小,以像素(宽度,高度)为单位。
# 它必须是“单元格大小”的整数倍,并且必须覆盖整个图像。
# 由于检测窗口必须是像元大小的整数倍,具体取决于您像元的大小,
# 因此生成的检测窗可能会比图像小一些。
# 完全可行
win_size = (x_cells * cell_size[0], y_cells * cell_size[1])
# 输出灰度图像的形状以供参考
print('\nThe gray scale image has shape: ', gray_pic.shape)
print()
# 输出HOG描述符的参数
print('HOG Descriptor Parameters:\n')
print('Window Size:', win_size)
print('Cell Size:', cell_size)
print('Block Size:', block_size)
print('Block Stride:', block_stride)
print('Number of Bins:', num_bins)
print()
# 使用上面定义的变量设置HOG描述符的参数
hog = cv2.HOGDescriptor(win_size, block_size, block_stride, cell_size, num_bins)
# 计算灰度图像的HOG描述符
hog_descriptor = hog.compute(gray_pic)
print(hog_descriptor.shape)
普通卷积/池化的输出尺寸与感受野计算公式
普通卷积的输出尺寸
设输入尺寸为 W × H W \times H W×H, 卷积核尺寸为 k × k k \times k k×k 步长为 S S S padding为 P P P
输出尺寸——H= H − k + 2 P S + 1 \frac{H-k+2P}{S}+1 SH−k+2P+1
输出尺寸——W= W − k + 2 P S + 1 \frac{W-k+2P}{S}+1 SW−k+2P+1
池化操作的输出尺寸
设输入尺寸为 W × H W \times H W×H, 池化核尺寸为 k × k k \times k k×k 步长为 S S S
输出尺寸——H= H − k S + 1 \frac{H-k}{S}+1 SH−k+1
输出尺寸——W= W − k S + 1 \frac{W-k}{S}+1 SW−k+1
卷积的感受野
这是一个自深到浅的过程,已知经过两层卷积(k=3,s=2,p=1)得到了一个 128 × 128 128\times128 128×128的特征图,请问这个特征图的感受野,则反向计算感受野:
R F N − 1 = f ( R F N , k e r n e l , s t r i d e ) = ( R F N − 1 ) × s t r i d e + k e r n e l RF_{N-1}=f(RF_N,kernel,stride)=(RF_N-1)\times stride + kernel RFN−1=f(RFN,kernel,stride)=(RFN−1)×stride+kernel
上述实例中即:(((1-1)*2+3)-1)*2+3=7
不同卷积的计算量与参数量
设输入特征图的shape为 H 1 × W 1 × C i n H_1\times W_1\times C_{in} H1×W1×Cin,卷积核大小为 k × k × C c i n k\times k \times C_{cin} k×k×Ccin,输出特征图的shape为 H 2 × W 2 × C o u t H_2\times W_2 \times C_{out} H2×W2×Cout。
常规卷积的计算量与参数量
计算量= k × k × C i n × H 2 × W 2 × C o u t k\times k\times C_{in}\times H_{2}\times W_{2} \times C_{out} k×k×Cin×H2×W2×Cout
参数量= k × k × C i n × C o u t k\times k\times C_{in}\times C_{out} k×k×Cin×Cout
分组卷积
计算量= k × k × C i n × H 2 × W 2 × C o u t × 1 g k\times k\times C_{in}\times H_{2}\times W_{2} \times C_{out}\times \frac{1}{g} k×k×Cin×H2×W2×Cout×g1
参数量= k × k × C i n × C o u t × 1 g k\times k\times C_{in}\times C_{out} \times \frac{1}{g} k×k×Cin×Cout×g1
深度可分解卷积的计算量与参数量
计算量= k × k × H 2 × W 2 × C i n + H 2 × W 2 × C o u t × C i n k\times k\times H_2\times W_2\times C_{in}+H_{2}\times W_{2} \times C_{out}\times C_{in} k×k×H2×W2×Cin+H2×W2×Cout×Cin
参数量= k × k × C i n + C i n × C o u t k\times k\times C_{in} +C_{in} \times C_{out} k×k×Cin+Cin×Cout
深度可分解卷积的计算量 常规卷积的计算量 = 1 C o u t + 1 k 2 \frac{深度可分解卷积的计算量}{常规卷积的计算量}=\frac{1}{C_{out}}+\frac{1}{k^2} 常规卷积的计算量深度可分解卷积的计算量=Cout1+k21
Batchnorm层的操作
输入: x = [ x ( 1 ) , x ( 2 ) , . . . , x ( m ) ] x= [x^{(1)},x^{(2)},...,x^{(m)}] x=[x(1),x(2),...,x(m)],其中 x ( i ) ∈ R n x^{(i)} \in R^{n} x(i)∈Rn 表示输入的第 i i i 个样本。
计算均值: μ = 1 m ∑ i = 1 m x ( i ) \mu = \frac{1}{m}\sum_{i=1}^{m} x^{(i)} μ=m1∑i=1mx(i)
计算方差: σ 2 = 1 m ∑ i = 1 m ( x ( i ) − μ ) 2 \sigma^{2} = \frac{1}{m}\sum_{i=1}^{m}(x^{(i)} - \mu)^{2} σ2=m1∑i=1m(x(i)−μ)2
归一化: x ^ ( i ) = x ( i ) − μ σ 2 + ϵ \hat{x}^{(i)} = \frac{x^{(i)} - \mu}{\sqrt{\sigma^{2} + \epsilon}} x^(i)=σ2+ϵx(i)−μ
其中 ϵ \epsilon ϵ 是一个非常小的数,避免分母为 0 0 0。
缩放和偏移: y ( i ) = γ x ^ ( i ) + β y^{(i)} = \gamma\hat{x}^{(i)} + \beta y(i)=γx^(i)+β
其中 γ \gamma γ 和 β \beta β 是可学习的参数,用于缩放和偏移归一化后的结果。
在训练过程中,每个 mini-batch 的均值和方差被计算,并用于归一化输入数据。在测试过程中,使用所有训练样本的均值和方差进行归一化。
Batchnorm层中可学习的参数
-
γ \gamma γ:缩放参数,用于对归一化后的特征进行缩放,增加网络的表达能力。
-
β \beta β:偏移参数,用于对归一化后的特征进行偏移,增加网络的表达能力。
这两个参数是通过反向传播算法进行训练得到的。在推理阶段,这些参数的值保持不变,因为它们用于对特征进行缩放和偏移,而这些特征是固定的。