Unity下平面反射实现
平面反射通常指的是在镜子或者光滑地面的反射效果上,如下图所示,

上图是一个光滑的平面,平面上的物体在平面上有对称的投影。
一、平面反射的原理
对于光照射到物体表面然后发生完美镜面反射的示意图,如下所示,

对于平面反射,假设平面上任意一点都会发生完美的镜面反射。因此,眼睛看到物体的一点的反射信息是从反射向量处得到的,这个可以用下图来表示,
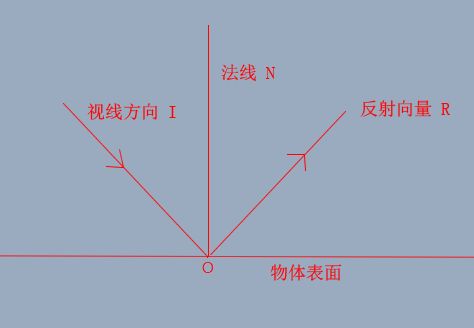
这个实际上相当于,眼睛从平面的下面看向反射向量,如下图所示,
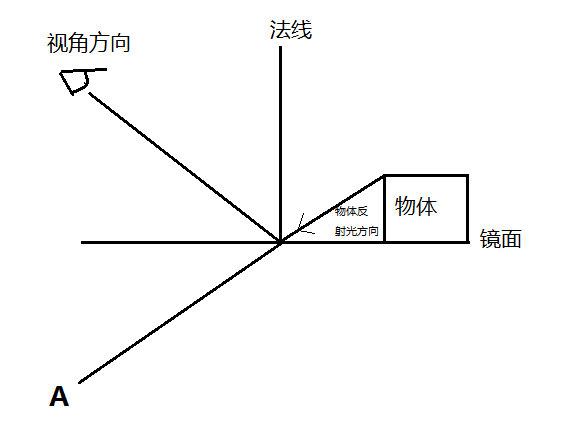
因此,如上图所示,我们可以把摄像机根据平面对称变换到A点所示的位置,然后再渲染一遍场景到RenderTexture中。当我们渲染点O的反射信息时候,就可以到这张RT中去采样了。那么如何去采样反射信息了?使用点O的屏幕空间坐标。因为,RT是从A点看到的场景,视线和平面的交点O是当前渲染的像素点,因此用O的屏幕空间坐标去采样RT就可以得到其反射信息。
1.1 平面反射矩阵
1.1.1 平面方程的计算
我们现在来推导一下把摄像机关于平面对称的反射矩阵。
我们知道一个平面可以表示为 P ∗ N + d = 0 P*N+d=0 P∗N+d=0。P是平面上任意一点,N是平面的法向量,d是一个常数。我们首先需要求出平面方程。对于平面,其世界空间的法向量就是N。用平面的世界空间位置带入P即可求出d的值。
plane = new Vector4(planeNormal.x, planeNormal.y, planeNormal.z, -Vector3.Dot(planeNormal, planePosition) - Offset);
我们可以用以上的一个Vector4表示一个平面,前三个分量表示normal,第四个分量表示d。
1.1.2 平面反射矩阵的计算

如上图所示,我们需要计算点A关于平面的对称点A’。关键在于计算出点A到平面的距离AO的大小。那么 A ′ = A − 2 ∗ n ∗ ∣ A O ∣ A'=A-2*n*|AO| A′=A−2∗n∗∣AO∣,负号是因为方向和法线相反。所以,关键是求出|AO|。因为AO实际上是AP在法线相反方向的投影向量,那么 ∣ A O ∣ = d o t ( A P , n ) = d o t ( A − P , n ) = d o t ( A , n ) − d o t ( P , n ) |AO|=dot(AP,n)=dot(A-P,n)=dot(A,n)-dot(P,n) ∣AO∣=dot(AP,n)=dot(A−P,n)=dot(A,n)−dot(P,n)。由于P满足平面方程,因此 d o t ( P , n ) = d dot(P,n)=d dot(P,n)=d,因此 ∣ A O ∣ = d o t ( A , n ) + d |AO|=dot(A,n)+d ∣AO∣=dot(A,n)+d,因此 A ′ = A − 2 ∗ n ∗ ( d o t ( A , n ) + d ) A'=A-2*n*(dot(A,n)+d) A′=A−2∗n∗(dot(A,n)+d)。
假设n为(nx,ny,nz),已知d的值,A是(x,y,z)点作为我们要变换的点,A’为(x’,y’,z‘),那么我们可以得到:
x ’ = x − 2 ( x ∗ n x + y ∗ n y + z ∗ n z + d ) ∗ n x = ( 1 − 2 n x ∗ n x ) x + ( − 2 n x ∗ n y ) y + ( − 2 n x ∗ n z ) z + ( − 2 d n x ) x’ = x - 2(x * nx + y * ny + z * nz + d)* nx = (1 - 2nx * nx)x +(-2nx * ny)y + (-2nx * nz)z + (-2dnx) x’=x−2(x∗nx+y∗ny+z∗nz+d)∗nx=(1−2nx∗nx)x+(−2nx∗ny)y+(−2nx∗nz)z+(−2dnx),
y ’ = y − 2 ( x ∗ n x + y ∗ n y + z ∗ n z + d ) ∗ n y = ( − 2 n x ∗ n y ) x + ( 1 − 2 n y ∗ n y ) y + ( − 2 n y ∗ n z ) z + ( − 2 d n y ) y’ = y - 2(x * nx + y * ny + z * nz + d)* ny = (-2nx * ny)x + (1 - 2ny * ny)y + (-2ny * nz)z + (-2dny) y’=y−2(x∗nx+y∗ny+z∗nz+d)∗ny=(−2nx∗ny)x+(1−2ny∗ny)y+(−2ny∗nz)z+(−2dny),
z ’ = z − 2 ( x ∗ n x + y ∗ n y + z ∗ n z + d ) ∗ n z = ( − 2 n x ∗ n z ) x + ( − 2 n y ∗ n z ) y + ( 1 − 2 n z ∗ n z ) z + ( − 2 d n z ) z’ = z - 2(x * nx + y * ny + z * nz + d)* nz = (-2nx * nz)x + (-2ny * nz)y + (1 - 2nz * nz)z + (-2dnz) z’=z−2(x∗nx+y∗ny+z∗nz+d)∗nz=(−2nx∗nz)x+(−2ny∗nz)y+(1−2nz∗nz)z+(−2dnz),
改写成矩阵形式可以得到平面反射的矩阵为:
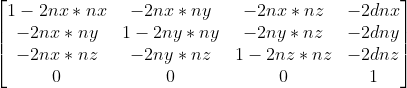
1.2 斜裁剪矩阵
上面我们已经推导出平面反射矩阵,不过还有一种特殊情况需要处理。
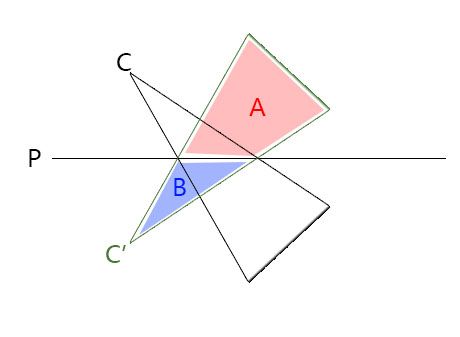
如上图所示,我们的平面是P,将摄像机从C点对称到C’点。从C’可以看到的区域包括A和B,但是B是在平面P的下部,我们从C是无法看到的。因此,从C’点渲染场景RT的时候必须排除B区域,也就是需要将平面P作为裁剪平面,裁剪掉区域B。
这个东西叫做斜裁剪矩阵,我们可以推导出具体的斜裁剪矩阵或者使用Unity提供的接口直接计算出来。
计算斜裁剪矩阵需要两个步骤,第一步是计算出摄像机空间下的平面表示,第二步是用摄像机空间下的平面和原投影矩阵一起计算斜投影矩阵。
具体推导可以参考文章,【图形与渲染】相机平面镜反射与斜裁剪矩阵(上)-镜像矩阵。
第二步也可以使用Unity的camera中的接口CalculateObliqueMatrix来计算,参数就是第一步得到的平面。
二、平面反射的实现
2.1 平面反射的脚本
这里的脚本指的是生成RenderTexture需要的脚本,脚本继承自MonoBehaviour。
2.1.1 默认管线下的实现
默认管线下需要在函数OnWillRenderObject中,基本步骤是先计算反射平面,然后计算反射矩阵和斜投影矩阵,设置反射相机的斜投影矩阵,然后将反射相机变换到平面对面,调用相机的Render函数渲染RT。需要注意的是,渲染的时候需要修改物体正反旋向,即GL.invertCulling设置为true。
2.1.2 Urp管线下的实现
Urp管线下,需要绑定 RenderPipelineManager.beginCameraRendering的回调,然后在回调中实现。回调中会接收到当前渲染的相机,反射相机就是该相机关于平面的镜像。同时,渲染RT的函数需要改成UniversalRenderPipeline.RenderSingleCamera,传入context和反射相机。其余步骤,跟默认管线的区别不大。
2.2 平面反射的Shader
平面反射的shader可以使用普通的场景shader做修改。关键在于如何采样平面反射信息和平面反射强度以及模糊等。
2.2.1 平面反射信息的采样
这个之前已经解释过用屏幕空间坐标来采样RT。
2.2.1 平面反射强度
这个可以用菲涅尔效应计算,不过关键点在于强度必须是NdotV的函数,最简单的方式是计算出NdotV,对NdotV取反或者1-NdotV,因为入射角越大反射光越强,同时提供一个最大最小值来限制强度范围。
2.2.1 模糊和Mipmap
可以采样周围多个像素然后做平均模糊或者高斯模糊。不过,最简单的方式是对RT强制生成Mipmap,采样RT的时候指定Mipmap级别。那么,mipmap级别如何计算了。我们可以根据shader的粗糙度来转行为mipmap级别,这个参考unity的urp内置shader函数PerceptualRoughnessToMipmapLevel的实现。
三、平面反射的优化
平面反射由于需要对场景镜像渲染一遍, DrawCall会翻倍,而且由于原理限制,没有有效的优化手段,因此平面反射通常是应用在特定的场合下。
优化的手段,主要是降低生成反射RT的消耗。
3.1 控制反射层级
我们可以在反射脚本中增加层级控制,然后设置反射相机的cullingMask,指定层级的物体才会被渲染到RT中。
3.2 控制反射RT的尺寸
可以根据反射平面的大小来调整RT的尺寸,同样我们可以在脚本中开放这个尺寸设置来方便美术来调整RT大小。
3.3 降低RT的shader复杂度
我们可以使用Unity的shader replacement将生成RT的shader都替换为一个简单的shader,然后再渲染生成RT,这样可以大幅度降低shader计算复杂度。不过,DrawCall是无法降低的。
参考资料
Unity Shader-反射效果(CubeMap,Reflection Probe,Planar Reflection,Screen Space Reflection)
图形与渲染】相机平面镜反射与斜裁剪矩阵(下)-斜裁剪矩阵
