数字图像处理 --- 相机的内参与外参（CV学习笔记）
Pinhole Camera Model（针孔相机模型）
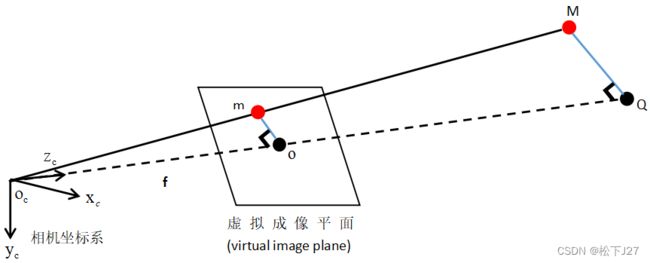
针孔相机是一种没有镜头、只有一个小光圈的简单相机。 光线穿过光圈并在相机的另一侧呈现倒立的图像。为了建模方便，我们可以把物理成像平面(image plane)上的图像移到实际场景(3D object)和焦点(focal point)之间，把他想象成一个和物理成像平面等大小的虚拟图像平面(Virtual image plane)，这样一来就不再是倒立的图像，而是直立图像。
有了相机后，上图中的蓝色盒子就变成了相机，上图中的物理成像平面Image plane也被数字化到由一个个pixel组成的sensor上，并保存下来。因此，对于相机而言，上图中的焦点就是相机的镜头，而上图中的物理成像平面，需要被转换成像素平面(pixel plane)，物理成像平面(image plane)与像素平面(pixel plane)大小相同，计量单位不同。物理成像平面的单位是一个物理单位，例如mm,，而像素平面实际上就是一个二维图像，他的单位实际上是某某pixel在图像中的第几行第几列。
为了后续的描述方便我们这里先定义四个坐标系：
1，二维像平面(焦平面)坐标系Image plane，原点为
，坐标轴用
,
表示。
2，二维图像坐标系pixel plane，原点为
，坐标轴用u,v表示。
3，三维相机坐标系pinhole plane/camera，原点为
，坐标轴用
，
，
表示。
4，三维世界坐标系world，原点为
，坐标轴用
，
，
表示。
将3D世界场景映射成2D图像(像素平面pixel plane)总共分两步，第一步是把定义在世界坐标系中的实际3D物体映射到3D相机极坐标系中。相当于是把实际世界中的物体分别通过两个不同的坐标系来表示，然后通过找到这两个不同坐标系之间的差异，建立这两个坐标系之间的联系。这一转换关系就是下图中到的转换。
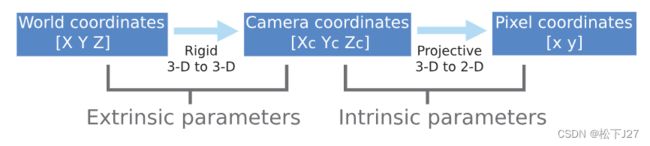
从3D世界坐标系(world coordinates)到3D相机坐标系(camera coordinates)，需要用到外参(extrinsic parameters)或外参矩阵(extrinsic matrix)--->[R t]。
其次，从3D相机坐标系(camera coordinates)到2D像素坐标系(pixel plane)需要用到内参(intrinsic parameters)或内参矩阵(intrinsic matrix)--->K。同样是把成像后的图像，用两个不同的坐标系来表示，然后再建立这两个坐标系(物理成像坐标系与二维图像坐标系)之间的联系，使两者可以相互转换。
extrinsic parameters外参：
对于世界坐标系中的某一点M而言，他本身是存在了，并不会因为我们有没有建立坐标系而受影响。但当我们人为的建立坐标系以后，这个点在我们所定义的坐标系下就有坐标值了。首先，对于点M而言，他在世界坐标系下可表示为M=[
]，而在相机坐标系中M=[
]，这是同一个点，只不过在不同的坐标系所对应的坐标值不同。(其中：
中的上角标“M”表示点M,下角标"w"表示世界坐标系worl，以此类推，关于下角标的定义可参照我上面定义的四个坐标系。)
相机坐标系相对于世界坐标系而言，我们不能保证两个坐标系的原点完全重合，因此，对于x-y-z都存在一定的位移，由一个3x1矩阵t(translation)表示，其中每个元素分别对应了x-y-z方向上的位移:
此外，我们也不能保证相机在拍照时没有任何角度的偏差，因此，这两个坐标系的坐标轴存在一个整体的旋转。由一个3x3矩阵R(rotation)表示：
二者合并得到增广矩阵[R|t]，使得:
![M=[R|t]\begin{bmatrix} x_{w}\\ y_{w}\\ z_{w} \end{bmatrix}=\begin{bmatrix} x_{c}\\ y_{c}\\ z_{c} \end{bmatrix}](http://img.e-com-net.com/image/info8/d6f3c9499a6343ec9d9c27e551bdefb6.png)
其中：
![[R|t]=\begin{bmatrix} r_{11} &r_{12} &r_{13} & t_{x}\\ r_{21} & r_{22} &r_{23} & t_{y} \\ r_{31} &r_{32} &r_{33} & t_{z} \end{bmatrix}](http://img.e-com-net.com/image/info8/abfaf8d7b4a24f4d9fe10fecb13ff3d9.png)
这一数学表达式的意义是：一个在世界坐标系中定义的点，如果要用相机坐标系来表示，可以用矩阵[R|t]左乘该点的世界坐标系坐标实现。这样一来就完成了世界坐标系到相机坐标系的转化。
Intrinsic parameters内参:
通过前面的研究，我们找到了世界坐标系与相机坐标系的联系，相当于学会了用相机坐标系来表示世界的物体(3D Object)，现在，我们用相机坐标系来分别描述世界中的实际物体与“挪到前面来的”物理成像平面中物体的像，即，在相机坐标系中用不同的坐标值定义了世界中的实际物体大M点与虚拟成像平面上的像---小m点(图一)，并找到他们之间的联系。
(图一)
表示光心，也叫摄影中心。过光心做垂直于物理成像平面的直线叫主光轴(principal axis)，垂点叫主点(principal point)。光心与主点之间的距离为焦距f。
现在，在相机坐标系中，我们令世界中的某一点大M的坐标值为M=[]。在虚拟成像平面中所成的像为小m，且小m的坐标值为m=[
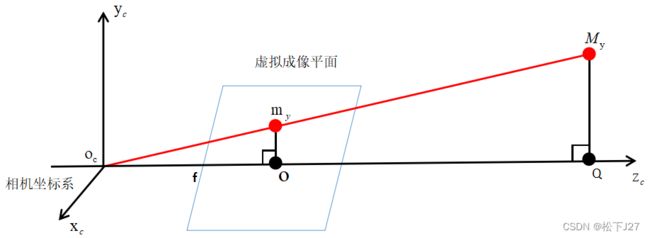
](注意：x-y-z的上角标，我用大写的M表示实际点大M所对应的坐标值，用小写的m表示虚拟成像平面中的点小m)。同时，我们令主光轴与相机坐标系中的轴重合，单看相机坐标系中由与轴组成的平面(图二)，我们令大M在这一平面上的投影为
，令小m在-平面上的投影为
。
(图二)
在三角形
中，线段
的长度为小m在轴方向的坐标值
，线段
的长度为小m在轴方向的坐标值
。在三角形
中，线段
的长度为
，线段
的长度为
。根据三角形与三角形相似，可以建立如下关系：
又因为小m点一定在物理成像平面上，则，在3D相机坐标系中，恒等于等于焦距f，代入上式后得出：
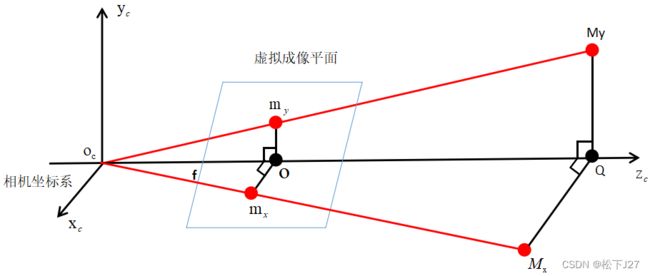
同样，如果单看相机坐标系中的与轴所组成的平面(见图三)，且用
表示大M在这一平面上的投影，用
表示小m在-平面上的投影：
根据相似相似三角形 
与三角形
，可以建立如下关系
这样一来，我们就建立了世界中的大M与虚拟成像平面上的对应点小m，在相机坐标系中的关系。
又因为，虚拟成像平面中的小m点，不仅在3D相机坐标系中，也在2D虚拟成像坐标系中。我们必须先找到两个坐标系的相对关系，继而找到小m点在虚拟成像坐标系中的坐标值。
已知相机坐标系中小m点的坐标值为m=[
，
，f]，在虚拟成像平面坐标系中点m的坐标值为m=[
，
]。对于这两个不同的坐标系，我们最先想到的是2D虚拟成像坐标系的中心=[
，
]可能不在主光轴上，即与相机坐标系下的光心O=[
，
]在2维平面中不是同一点，而是存在一定偏差，即：
这两个式子的意义是：偏离了主光轴的中心和光心加上一定的偏移量表示的是同一个点。
又因为，在相机内部，物理成像平面被sensor以pixel为单位采样了，因此，需要一个由mm为单位的相机坐标系(image plane)到以pixel为单位的图像坐标系(pixel plane)之间的转换。且，二维图像坐标系的起点往往是图像的左上角。因此，在这一转换中还需要加一个x,y方向的偏移量Offset。
假设图像传感器的物理尺寸，也就是物理成像平面的大小为mxn(单位mm)，传感器保存的图像尺寸为wxh(单位pixel)。要想把mxn的小图保存到wxh个pixel上，需要建立一个以mm为单位的物理成像平面与以pixel为单位的图像之间的对应关系，即：
表示每个pixel占多少mm。
这样一来由相机坐标系，，表示的实际3D场景，就转化为了物理成像平面上：
参考文献：
1，https://www.cnblogs.com/xiaohuidi/p/15711767.html
2，What Is Camera Calibration?- MATLAB & Simulink- MathWorks 中国
3，2.3 透视投影的相机模型_哔哩哔哩_bilibili
版权声明：文中的部分图片，文字或者其他素材，可能来自很多不同的网站和说明，在此没法一一列出，如有侵权，请告知，立即删除。欢迎大家转载，但是，如果有人引用或者COPY我的文章，必须在你的文章中注明你所使用的图片或者文字来自于我的文章，否则，侵权必究。 ----松下J27