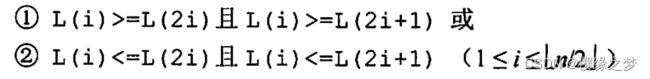数据结构——排序【仅用于考试】
1、简介
排序,是重新排列表中的元素,使表中的元素满足按关键字有序的过程
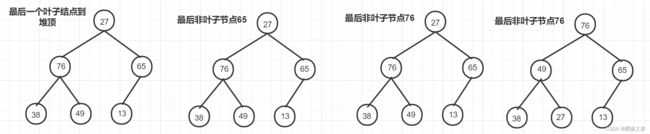
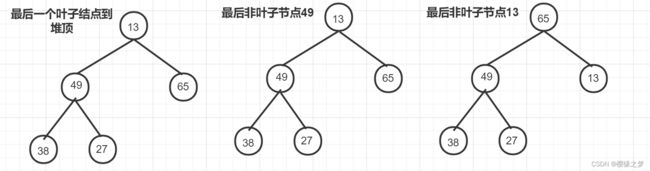
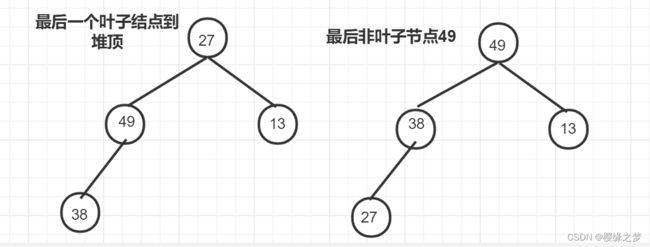
稳定性:选取两个元素Ri 不稳定的排序:【简单选择排序,快速排序,堆排序、希尔排序】 内部排序:指在排序期间元素都在内存中的排序, 外部排序:指在排序期间元素在内外存之间移动的排序,如:多路归并排序 希尔排序:平均o(n^1.3),最坏o(n^2),最好o(n) 2、各类排序算法 2.1 插入排序 基本思想:每次将一个待排序的记录按其关键字大小插入前面已经排好序的子序列,直到所有记录插入完成。 过程: 例子(49,38,65,97,76,13,27,49(1))【49和49(1)的值一样,为了区分标记】 选定[49]为排好序的子序列,按照上述算法进行排序: i=1(初始值):[49], 38 , 65 , 97 , 76 , 13 , 27 , 49(1) i=2: [38 ,49] , 65 , 97 , 76 , 13 , 27 , 49(1) i=3: [38 ,49, 65] , 97 , 76 , 13 , 27 , 49(1) i=4: [38 , 49, 65 , 97] , 76 , 13 , 27 , 49(1) i=5: [38 ,49 , 65 , 76 , 97] , 13 , 27 , 49(1) i=6: [ 13 ,38 ,49 , 65 , 76 , 97] , 27 , 49(1) i=7: [ 13 ,27 , 38 ,49 , 65 , 76 , 97], 49(1) i=8: [ 13 ,27 , 38 ,49 , 49(1) 65 , 76 , 97] 2.2 折半插入排序 折半插入算法仅减少了比较元素的次数,该比较次数与待排序表的初始状态无关,仅取决于表中的元素个数,而元素的移动次数未变,与待排序表的初始状态有关。 2.3 希尔排序 基本思想:先将待排序分割成若干子表,间隔为d,对各个子表进行直接插入排序,然后减少间隔d,直到d<1,然后再对全体记录记录进行一次直接插入排序。 过程:( 49,38,65,97,76,13,27,40,55,04),d=5,则子序列为 (49,13)[排序]--->(49,13),交换 (38,27)[排序]--->(38,27)不交换 (65,40)[排序]--->(65,40),交换 (97,55)[排序]--->(97,55),交换 (76,04)[排序]--->(76,04),交换 第一趟结果为:13,27,40, 55,04, 49,38,65,97,76 第二趟d=3: (13,55,38,76)->(13,3,8,55,76) (27,04,65)->(04,27,65) (40,49,97)->(40,49,97) 结果为:13,04,40,38,27,49,55,65,97,76 第三趟(d=1):04,13,27,38,40,49,55,65,76,97[直接插入排序] 应用场景:线性表为顺序存储的情况 2.4 冒泡排序 冒泡排序的基本思想是从前往后(从后往前)两两比较相邻元素的值,若为逆序,则交换,直到序列比较完成,这个叫第一趟冒泡排序,将最小的元素交换到待排序列的第一个位置。 过程: 2.5 快速排序 快速排序【递归工作栈】是基于分治法的,从当前参加排序的元素中任选一个元素(通常称之为分界元素)与当前参加排序的那些元素进行比较,凡是小于分界元素的元素都移到分界元素的前面,凡是大于分界元的元素都移到分界元素的后面,分界元素将当前参加排序的元素分成前后两部分,而分界元素处在排序的最终位置。然后,分别对这两部分中大小大于1的部分重复上述过程,直到排序结束。 采用递归方式进行快排,递归次数与每次划分后得到的分区处理顺序无关,递归次数与初始数据的排列次序有关,对分区的长短处理顺序,影响的是递归时对栈的使用内存 过程:(49,38,65,97,76,13,27)选取分界元素49,并定义low=0,high=n-1(6)指向序列头尾 第一趟[i=2,j=6]:49,38,65,97,76,13,27--->27,38,49,97,76,13,65(low找到65,high找到13,并进行交换) [i=3,j=5] 27,38,49,97,76,13,65---> 27,38,13,49,76,97,65 [第一趟结束,分割为两个序列,] 第二趟(左序列):{27,38,13},49,{65,97,76}--->13,27,38(选分界元素27,low找到38,high找到13,并进行交换) (右序列):{76,97,65}--->{65,76,97}(选分界元素76,low找到97,high找到65,并进行交换) 快排的运行时间和划分是否对称有关, 2.6 简单选择排序 简单选择排序是假设排序表为L,长度为n,第i趟排序就是从L[i...n]中选择关键字最小的元素与L[i]交换,每一趟排序可以确定一个元素的最终位置。 过程:(49,38,65,97,76,13,27)以49为基准 第一趟:13,38,65,97,76,49,27 ,以38为基准 第二趟:13,27,65,97,76,49,38 ,以65为基准 第三趟:13,27,38,97,76,49,65 ,以97为基准 第四趟:13,27,38,49,76,97,65 ,以76为基准 第五趟:13,27,65,97,65,97,76 ,以97为基准 第六趟:13,27,65,97,65,76,97 简单选择排序算法的元素移动次数较少,不会超过3(n-1),元素的比较次数与初始状态无关。 2.7 堆排序 n个关键字序列,且满足条件①为大根堆,满足条件②是小根堆,堆是一棵完全二叉树。 堆排序是将n个待排序元素建成初始化堆,由于堆本身的特点,堆顶元素为最值,输出堆顶元素之后,将堆底元素送入堆顶,再进行堆调整。 基本思想: 1、按照层次遍历将待排序元素初始化为一棵完全二叉树; 2、找到最后一个非叶子节点,进行非叶子节点和该结点的叶子结点进行比较,如果叶子结点大于非叶子节点,需要交换,没有就不交换 3、继续遍历其他非叶子节点,如果交换之后的子树存在不满足于堆的性质,也需要进行交换,直到遍历所有非叶子结点,找到最大值,将最大值取出,并将二叉树的最后一个叶子结点填充到堆顶,并继续进行交换过程,直到只剩一个结点,该序列就是排序之后的结果。 过程(大根堆): 例:(49,38,65,97,76,13,27) 列表输出[97] 列表输出[97,76] 列表输出[97,76,65,49] 最终列表输出[97,76,65,49,38,27,13] 2.8归并排序 归并排序是将两个或两个以上的有序表组合成一个新的有序表,以二路归并排序为例,假定待排序数组的长度为n,可将视为有n个有序子表,两两归并,得到 例:(49,38,65,97,76,13,27) 初始值:[49] ,[38] ,[65] ,[97] ,[76] ,[13] ,[27] 第一趟:[49,38] ,[65,97] ,[76 ,13] ,[27] --->[38,49] ,[65,97] ,[13 ,76] ,[27] 第二趟:[38,49,65,97] ,[13 ,76,27] --->[38,49,65,97] ,[13,27,76] 第三趟:[38,49,65,97] ,[13,27,76] --->[13,27,38,49,65,76,97] 空间:o(n) 时间:每趟归并的时间复杂度o(n),归并次数o(log2n),总时间复杂度o(nlog2n) 3、例题 3.1 选择题 3.2 简单题![]() 个长度为2或1的有序表,在两两归并,直到合并后为一个长度为n的有序表为止。
个长度为2或1的有序表,在两两归并,直到合并后为一个长度为n的有序表为止。
[n/2]+2位置上(分析堆是完全二叉树,假设有h层,前h-1层的节点数是2^(h-1)-1,那2^(h-1)<=n)