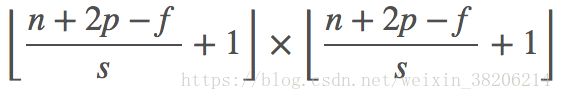神经网络基础-卷积神经网络

在深度学习的路上，从头开始了解一下各项技术。本人是DL小白，连续记录我自己看的一些东西，大家可以互相交流。

本文参考：本文参考吴恩达老师的Coursera深度学习课程，很棒的课，推荐 

本文默认你已经大致了解深度学习的简单概念，如果需要更简单的例子，可以参考吴恩达老师的入门课程：

http://study.163.com/courses-search?keyword=%E5%90%B4%E6%81%A9%E8%BE%BE#/?ot=5

转载请注明出处，其他的随你便咯

一、前言

卷积神经网络(Convolutional Neural Network, CNN)是一种深度前馈人工神经网络，已成功地应用于图像识别领域，同时在声纹识别领域，也取得了不小的成果。

二、卷积运算

卷积运算是卷积神经网络的基本组成部分，我们用边缘检测的例子来说明一下卷积运算的过程。

在下图中，我们通过垂直边缘检测和水平边缘检测，可以获得右边的图像：

即，仅保留图片中的垂直边缘或水平边缘。

垂直边缘检测：

假设一张图片的大小为 6×6(数字表示图片大小，具体为像素值)，和一个3×3的filter(卷积核)进行卷积运算，用“*”符号表示。图片和垂直边缘检测器分别如图中左1矩阵和左2矩阵：

卷积运算的过程，实际上是让filter从图片左上角开始不断移动，不断地和其大小相同的部分做对应元素的乘法运算并求和，最终得到的数字相当于新图片的一个像素值，如右矩阵所示，最终得到一个 4×4 大小的图片。这个过程即为卷积运算。

PS.给出卷积纬度计算公式：

图片为 n×n 大小，filter为 f×f 大小，结果为(n - f + 1)×(n - f + 1)

三、填充(Padding)

在卷积运算的过程中，我们发现了如下的问题：

• 每次卷积操作，会让图片缩小；
  • 如例子中，6×6的图片，经过 3×3 filter的卷积后，只剩下4×4 大小
• 角落和边缘位置的像素在卷积运算的过程中，参与的次数很少，最终结果中，可能会损失数据。

为了解决如上的两个问题，我们在进行卷积运算前，为图片加Padding，包围角落和边缘的像素，使得通过filter的卷积运算后，图片大小不变，也不会丢失角落和边缘的信息。Padding的过程如图所示：

用p来表示Padding的值，当输入为n×n大小的图片，最终得到的图片大小为(n + 2p − f + 1)×(n + 2p − f + 1)，为了让图片大小保持不变，需根据filter的大小f来调整p的值。根据是否使用Padding我们可以将卷积分为两种。

Valid / Same 卷积：

• Valid卷积：没有padding，输入n×n的图像，输出(n - f + 1)×(n - f + 1)的图像；
• Same卷积：有padding，输出与输入图片大小相同，p = (f - 1) / 2。

四、卷积步长(stride)

卷积的步长是构建CNN的一个基本的属性。在上述的例子里面，我们使用的步长 stride = 1，即每次filter移动一个像素。当stride = 2时，卷积运算如下：

即每次filter在计算完一个数值时，会移动两个像素的位移，继续计算下一个数值。

我们用s表示stride步长的大小，那么在进行卷积运算后，图片从n×n大小，变为如下大小：

五、立体卷积

在上面的例子和介绍中，我们的图像都是二维的。在应用于彩色图像时，我们用RGB三通道来表示一张图片。其中R红色，G绿色和B蓝色，该表示法是用三个三原色的数值，来组合成一个图片。当我们对彩色图片进行卷积的时候，此时的卷积核应为三维卷积核。

其实与二维的卷积类似，只是我们现在的filter与图片的维度保持一致，卷积核的第三个维度需要与图片保持一致，在计算之后求和的过程，是f × f × f个数字之和。

多卷积核

单个卷积核应用于图片时，可以提取特定的特征。我们也可以同时用多个卷积核来同时提取不同的特征：

在上图中，我们用了两个3×3×3的卷积核分别提取了图片的垂直边缘和水平边缘，最终得到了2通道的4×4的特征图片。

总结而言：

输入的图片表示为：n×n×nc(通道数)

卷积核为：f×f×nc(与图标通道数一致)

运算结果为：(n − f + 1)×(n − f + 1)×nc

六、简单卷积网络

卷积神经网络和普通的神经网络前向传播的过程类似。如下图所示：

CNN也是先由输入和权重做线性运算，然后将结果送进一个激活函数，得到最终的输出，不同点在于卷积神经网络中，权重是filter，输入是多维度的矩阵，二者进行卷积运算。

单层卷积的参数个数

在一个卷积层中，假设我们有10个3×3×3的卷积核，每个卷积核有1个偏置，那么对于一个卷积层的参数个数为：

(3×3×3+1) ×10 = 280

那么，无论图片的有多大，上例中的卷积层的参数是固定的280个，相对与普通的深度神经网络而言，卷积神经网络的参数少了很多。

标记总结：

如果 l 表示一个卷积层：

卷积网络示例：

一个卷积网络，通常由多个卷积层组合而成，下面我们给出一个例子，方便大家理解：

在上述例子中，除了卷积层，我们还加入了池化层(POOL)和全连接层(FC)。

七、池化层(POOL)

池化层是CNN中的一个重要概念，一般是在卷积层之后。池化层用来对输入进行降采样，降低维度并保留显著的参数。其特点是输出一个固定大小的矩阵，并且降低输出结果的维度。

最大池化(Max Pooling)

最大池化层是对前一层得到的特征图进行池化减小，仅由当前小区域内的最大值来代表赤化后的值。

如上图所示，我们将原有的矩阵划分为4个区域，每个区域仅取其最大值做代表。

在最大池化中，有一组超参数需要进行调整。其中，f表示池化的大小，s表示步长。

池化前：n×n ；

池化后：。

平均池化(Average Pooling)

平均池化与最大池化的唯一不同是其选取的是小区域内的均值来代表该区域内的值。

 

总结而言

池化层的超参数：

PS.池化层中一般不用Padding，并且池化层没有需要学习的参数。

八、基于Tensorflow的CNN实现

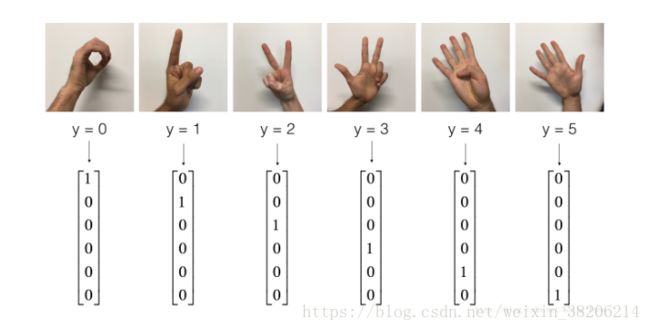
接下来，我们基于TensorFlow模型，来实现一个简单CNN。在这个例子中，我们将用一个CNN来识别0-5的图像：

上图为我们实现的数据集。

加载包

import math
import numpy as np
import h5py
import matplotlib.pyplot as plt
import scipy
from PIL import Image
from scipy import ndimage
import tensorflow as tf
from tensorflow.python.framework import ops
from cnn_utils import *

%matplotlib inline
np.random.seed(1)

# 下载数据集(signs)
X_train_orig, Y_train_orig, X_test_orig, Y_test_orig, classes = load_dataset()

数据集

接下来，我们可以看一下该数据集的形状：

X_train = X_train_orig/255.
X_test = X_test_orig/255.
Y_train = convert_to_one_hot(Y_train_orig, 6).T
Y_test = convert_to_one_hot(Y_test_orig, 6).T
print ("number of training examples = " + str(X_train.shape[0]))
print ("number of test examples = " + str(X_test.shape[0]))
print ("X_train shape: " + str(X_train.shape))
print ("Y_train shape: " + str(Y_train.shape))
print ("X_test shape: " + str(X_test.shape))
print ("Y_test shape: " + str(Y_test.shape))
conv_layers = {}

输出值为：

number of training examples = 1080
number of test examples = 120
X_train shape: (1080, 64, 64, 3)
Y_train shape: (1080, 6)
X_test shape: (120, 64, 64, 3)
Y_test shape: (120, 6)

可以看出X为(1080，64，64，3)，对应1080个样本，每个样本形状为64×64×3。

1、创建占位符placeholder

在TensorFlow模型中，我们需要为输入数据创建占位符，并在Session中传入模型中。

因为我们在训练、测试中，使用的数据量不同，所以我们可以将X，Y的维度设定为[None, n_h0, n_w0, n_c0]和[None, n_y]。

def create_placeholders(n_H0, n_W0, n_C0, n_y):
     """
    Creates the placeholders for the tensorflow session.

    Arguments:
    n_H0 -- scalar, height of an input image
    n_W0 -- scalar, width of an input image
    n_C0 -- scalar, number of channels of the input
    n_y -- scalar, number of classes

    Returns:
    X -- placeholder for the data input, of shape [None, n_H0, n_W0, n_C0] and dtype "float"
    Y -- placeholder for the input labels, of shape [None, n_y] and dtype "float"
    """
    
    X = tf.placeholder(tf.float32, shape = [None, n_H0, n_W0, n_C0])
    Y = tf.placeholder(tf.float32, shape = [None, n_y])

    return X, Y

2、初始化参数

我们需要初始化filter(卷积核)，在TensorFlow模型中，我们可以用

tf.contrib.layers.xavier_initializer(seed = 0)

对于b(偏置)，TensorFlow模型会自动处理。

def initialize_parameters():
    """
    Initializes weight parameters to build a neural network with tensorflow. The shapes are:
                        W1 : [4, 4, 3, 8]
                        W2 : [2, 2, 8, 16]
    Returns:
    parameters -- a dictionary of tensors containing W1, W2
    """
    
    tf.set_random_seed() #为了让最终结果一致，自己实现时可以随即设置

    W1 = tf.get_variable("W1", [4, 4, 3, 8], initlializer = tf.contrib.layers.xavier_initializer(seed = 0))
    W2 = tf.get_variable("W2", [2, 2, 8, 16], initlializer = tf.contrib.layers.xavier_initializer(seed = 0))

    parameters = {"W1": W1,
                  "W2": W2}

    return parameters

3、前向传播

在TensorFlow模型中，最好的一点是我们可以使用内置函数来执行卷积步骤。

tf.nn.conv2d(X, W1, strides = [1, s, s, 1], padding = 'SAME')：其中X为输入值，W1为filter，步长为s，padding的类型是SAME卷积。

tf.nn.max_pool(A, ksize = [1, f, f, 1], strides = [1, s, s, 1], padding = 'SAME')：其中A为输入值，用窗口大小为(f, f)和步长(s, s)，在每个窗口上进行最大池化。

tf.nn.relu(Z1)：计算Z1的ReLU，激活函数。

tf.contrib.layers.flatten(P)：其中输入为P，将输入展开为一个一维向量，形状为[batch_size, k]。

tf.contrib.layers.fully_connected(F, num_outputs)：给定一个一维向量F，返回使用全连接的层计算的输出值。(模型会自定义初始值)

我们将构建如下模型：

CONV2D(卷积层) -> ReLU(激活函数) -> MAXPOOL(最大赤化层) -> CONV2D -> ReLU -> MAXPOOL -> FLATTEN -> FULLYCONNECTED

def forward_propagation(X, parameters):
     """
    Implements the forward propagation for the model:
    CONV2D -> RELU -> MAXPOOL -> CONV2D -> RELU -> MAXPOOL -> FLATTEN -> FULLYCONNECTED

    Arguments:
    X -- input dataset placeholder, of shape (input size, number of examples)
    parameters -- python dictionary containing your parameters "W1", "W2"
                  the shapes are given in initialize_parameters

    Returns:
    Z3 -- the output of the last LINEAR unit
    """

    W1 = parameters['W1']
    W2 = parameters['W2']

    #CONV2D: strides = 1, padding = 'SAME'
    Z1 = tf.nn.conv2d(X, W1, strides = [1, 1, 1, 1], padding = 'SAME')
    #ReLU
    A1 = tf.nn.relu(Z1)
    #MAXPOOL: windows = (8, 8)，strides = 8, padding = 'SAME'
    P1 = tf.nn.max_pool(A1, ksize = [1, 8, 8, 1], strides = [1, 8, 8, 1], padding = 'SAME')
    # CONV2D: stride = 1, padding = 'SAME'
    Z2 = tf.nn.conv2d(P1, W2, strides=[1,1,1,1], padding='SAME')
    # ReLU
    A2 = tf.nn.relu(Z2)
    # MAXPOOL: window = (4, 4), stride = 4, padding = 'SAME'
    P2 = tf.nn.max_pool(A2, ksize=[1,4,4,1], strides=[1,4,4,1], padding='SAME')
    # FLATTEN
    P2 = tf.contrib.layers.flatten(P2)
    # FULLY-CONNECTED 6个结点，没有激活函数
    Z3 = tf.contrib.layers.fully_connected(P2, 6, activation_fn=None)

    return Z3

4、计算成本

在CNN中，我们也使用代价函数，来优化模型。可以使用到如下的内置函数：

tf.nn.softmax_entropy_with_logits(logits = Z3, labels = Y)：计算softmax的熵损失。即能计算softmax激活函数，也能计算损失函数，logits为输入值，labels为真实样本标签。

tf.reduce_mean：计算元素均值，可以计算所有损失函数，可以得到代价函数。

def compute_cost(Z3, Y):
     """
    Computes the cost

    Arguments:
    Z3 -- output of forward propagation (output of the last LINEAR unit), of shape (6, number of examples)
    Y -- "true" labels vector placeholder, same shape as Z3

    Returns:
    cost - Tensor of the cost function
    """

    cost = tf.reduce_mean(tf.nn.softmax_cross_entropy_with_logits(logits = Z3, labels = Y))

    return cost

5、构建模型

模型应该实现如下功能：

• 创建占位符
• 初始化参数
• 向前传播
• 计算成本
• 创建一个优化器

其中，在该模型中用到了random_mini_batches()，这个是小批量梯度下降法，思想是在每一次只用一个批量的数据来进行前向和反向的调整，这样可以提高训练速度。

def model(X_train, Y_train, X_test, Y_test, learning_rate = 0.009,
          num_epochs = 100, minibatch_size = 64, print_cost = True):
    """
    Implements a three-layer ConvNet in Tensorflow:
    CONV2D -> RELU -> MAXPOOL -> CONV2D -> RELU -> MAXPOOL -> FLATTEN -> FULLYCONNECTED

    Arguments:
    X_train -- training set, of shape (None, 64, 64, 3)
    Y_train -- test set, of shape (None, n_y = 6)
    X_test -- training set, of shape (None, 64, 64, 3)
    Y_test -- test set, of shape (None, n_y = 6)
    learning_rate -- learning rate of the optimization
    num_epochs -- number of epochs of the optimization loop
    minibatch_size -- size of a minibatch
    print_cost -- True to print the cost every 100 epochs

    Returns:
    train_accuracy -- real number, accuracy on the train set (X_train)
    test_accuracy -- real number, testing accuracy on the test set (X_test)
    parameters -- parameters learnt by the model. They can then be used to predict.
    """

    ops.reset_default_graph()                        # 可以让我们在每次调用模型时，初始化参数
    tf.set_random_seed(1)                            # 确保输出值，与我们提供的样例一致
    seed = 3                                         
    (m, n_H0, n_W0, n_C0) = X_train.shape             
    n_y = Y_train.shape[1]                            
    costs = []                                       # 保存cost的缓存

    #创建placeholder
    X, Y = create_placeholder(n_H0, n_W0, n_C0, n_y)

    #初始化参数
    parameters = initialize_parameters()

    #前向传播
    Z3 = forward_propagation(X, parameters)

    #计算损失函数
    cost = compute_cost(Z3)

    #BP算法
    optimizer = tf.train.AdamOptimizer(learning_rate).minimize(cost)

    #初始化所有张量，运行计算图
    init = tf.global_variables_initializer()
    with tf.Session() as sess:
        sess.run(init)
        #循环训练CNN
        for epoch in range(num_epochs):
            
            minibatch_cost = 0.
            num_minibatches = int(m / minibatch_size)
            seed = seed + 1 #每次minibatch都有不同的seed，保证每次训练样本顺序都不一致
            minibatches = random_mini_batches(X_train, Y_train, minibatch_size, seed)
            
            for minibatch in minibatches:
                (minibatch_X, minibatch_Y) = minibatch
                
                _, temp_cost = sess.run([optimizer, cost], feed_dict = {X: minibatch_X, minibatch_Y})

                minibatch_cost += temp_cost / num_minibatches
 
            # 每5次打印出损失函数
            if print_cost == True and epoch % 5 == 0:
                print ("Cost after epoch %i: %f" % (epoch, minibatch_cost))
            if print_cost == True and epoch % 1 == 0:
                costs.append(minibatch_cost)

        # 画出损失函数的图像
        plt.plot(np.squeeze(costs))
        plt.ylabel('cost')
        plt.xlabel('iterations (per tens)')
        plt.title("Learning rate =" + str(learning_rate))
        plt.show()

        # 预测函数
        predict_op = tf.argmax(Z3, 1)
        correct_prediction = tf.equal(predict_op, tf.argmax(Y, 1))

        # 测试集的效果计算
        accuracy = tf.reduce_mean(tf.cast(correct_prediction, "float"))
        print(accuracy)
        train_accuracy = accuracy.eval({X: X_train, Y: Y_train})
        test_accuracy = accuracy.eval({X: X_test, Y: Y_test})
        print("Train Accuracy:", train_accuracy)
        print("Test Accuracy:", test_accuracy)

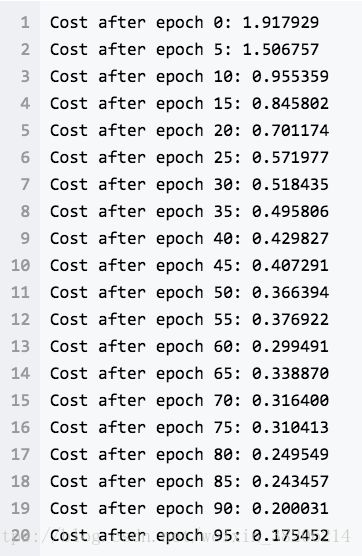
        return train_accuracy, test_accuracy, parameters

 接下来，如果一切都工作正常，我们会得到如下结果：

我们可以看到损失一直在下降，损失图像如下：

总结而言：

卷积神经网络(CNN)实际上，是在输入后，先对输入值进行提取特征，并对特征进行处理(池化)。这个过程不仅提取了过程，也让特征值更显著，更容易被我们学习，之后再进行全连接，得到我们的输出值。CNN对比普通NN而言，减少了参数个数，加快了训练速度，与此同时也提高了识别效果。