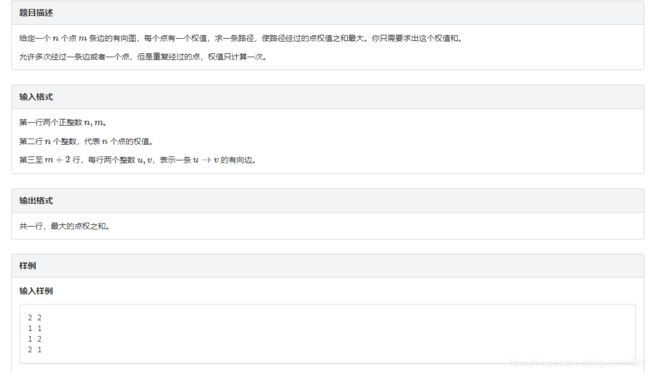
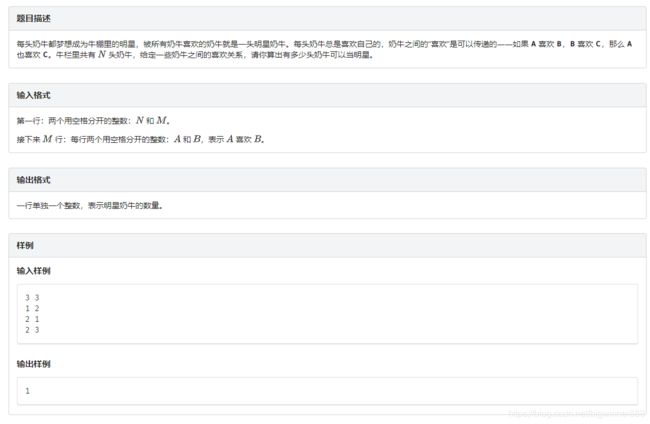
第三部分 图论算法 （第四章 强连通分量）例题

例题一： 有向图缩点 link

思路：
大家一开始可能都会想到直接用SPFA跑最长路，时间复杂度为$O(nm)$，
看看数据，TLE是必然的。
那有没有时间更优的方法——强连通分量。

分析题意，每个点点权只被计算一次，允许一条边走多次，
那我们考虑用Tarjan来进行缩点，
使图变成有向无环图，再进行$DP$。
设转移方程为：$$f=max(f_u+di{s}_v,f_v)$$
$f_i$表示以i作为终点的路径所经过的最大点权和。

#include
#include
#include

using namespace std;

const int N = 1e5 + 10;
struct node {int to, nxt;} e[N], e_[N];
int n, m, a[N], head[N], KK, tot;
int x, y, dfn[N], low[N], num, in[N], ans;
int sum[N], head_[N], KK_, du[N], dis[N];
queue <int> q;
stack <int> s;

void add(int x, int y) {e[++KK] = (node){y, head[x]}; head[x] = KK;}

void add_(int x, int y) {e_[++KK_] = (node){y, head_[x]}; head_[x] = KK_;}

void Tarjan(int now) 
{
	dfn[now] = low[now] = ++num;
	s.push(now);
	for (int i = head[now]; i; i = e[i].nxt)
		if (!dfn[e[i].to]) Tarjan(e[i].to), low[now] = min(low[now], low[e[i].to]);
		else if (!in[e[i].to]) low[now] = min(low[now], low[e[i].to]);
	
	if (dfn[now] == low[now])
	{
		in[now] = ++tot;
		sum[tot] = a[now];
		int tmp = s.top();
		while (tmp != now) s.pop(),in[tmp] = tot,sum[tot] += a[tmp], tmp = s.top();
		s.pop();
	}
}

int main() {
	scanf("%d %d", &n, &m);
	for (int i = 1; i <= n; i++) scanf("%d", &a[i]);
	for (int i = 1; i <= m; i++) scanf("%d %d", &x, &y), add(x, y);
	for (int i = 1; i <= n; i++)
		if (!dfn[i]) Tarjan(i);
	for (int i = 1; i <= n; i++)
	 for (int j = head[i]; j; j = e[j].nxt)
	 {
	 	int to = e[j].to;
	 	if (in[i] != in[to]) 
			add_(in[i], in[to]), du[in[to]]++;	
	 }
	
	for (int i = 1; i <= tot; i++)
		if (!du[i]) 
			q.push(i), dis[i] = sum[i];
	while (!q.empty()) 
	{
		int now = q.front();
		q.pop();
		for (int i = head_[now]; i; i = e_[i].nxt) 
		{
			dis[e_[i].to] = max(dis[e_[i].to], dis[now] + sum[e_[i].to]);
			du[e_[i].to]--;
			if (!du[e_[i].to]) q.push(e_[i].to);
		}
	}
	
	for (int i = 1; i <= tot; i++)
		ans = max(ans, dis[i]);
	printf("%d", ans);
	return 0;
}

例题二： 受欢迎的牛 link

思路：
由题可得，受欢迎的奶牛只有可能是图中唯一的出度为零的强连通分量中的所有奶牛，
所以若出现两个以上出度为0的强连通分量则不存在明星奶牛，
因为那几个出度为零的分量的爱慕无法传递出去。
那唯一的分量能受到其他分量的爱慕同时在分量内相互传递，
所以该分量中的所有奶牛都是明星。

#include 
#include 
#include 

using namespace std;

const int N = 5e4 + 10;
struct node {int to, next;} e[N];
int n, m, dfn[N], low[N], cnt, head[N], in[N], sum[N], tot, du[N], flag, ans, x, y;
stack <int> s;

void add(int x, int y) {e[++cnt] = (node){y, head[x]}, head[x] = cnt;}

void Tarjan(int now)
{
	low[now] = dfn[now] = ++cnt;
	s.push(now);
	for(int i = head[now]; i; i = e[i].next)
	{
		int to = e[i].to;
		if(!dfn[to]) Tarjan(to), low[now] = min(low[to], low[now]);
		else if(!in[to]) low[now] = min(low[to], low[now]);
	}
	if(dfn[now] == low[now])
	{
		in[now] = ++tot;
		sum[tot] = 1;
		int tmp = s.top();
		while(tmp != now) s.pop(), in[tmp] = tot, sum[tot]++, tmp = s.top();
		s.pop();
	}
}

int  main()
{
	scanf("%d%d", &n, &m);
	for(int i = 1; i <= m; i++) scanf("%d%d", &x, &y), add(x, y);
	cnt = 0;
	for(int i = 1; i <= n; i++) 
		if(!dfn[i]) Tarjan(i);
	for(int i = 1; i <= n; i++)
	 for(int j = head[i]; j; j = e[j].next)
	 {
		int to = e[j].to;
		if(in[i] != in[to]) du[in[i]]++;
	 }
	for(int i = 1; i <= tot; i++)
		if(!du[i]) ans = sum[i], flag++;
	if(flag != 1) printf("0\n");
	else printf("%d\n", ans);
 	return 0;
}

例题三： 最大半联通子图 link

题目大意：

我们称一个子图是半连通子图，
就是这个子图的任意两个点之间都有路径从一个点到另一个点。（只要能从任意一边到另一边即可）
问你一个图的最大半连通子图是多大，这样的图有多少个，
个数对一个给出的数取模。

思路：
首先，我们发现强连通分量的定义与最大半连通子图有些相似。
进一步地，发现强连通分量就是一个半连通子图。
所以我们考虑将原图进行缩点，得到一张DAG，
然后找一条路径最大的链就可以了。
得到最长的长度后，然后要看有多少条。
那你再 dfs 跑一次，想最短路的找路径一样弄。

#include 
using namespace std;
const int N=1e5+5,M=1e6+5;

int n,m,MOD,cnt,ans,MAX,k,now1,now2;
int head[N],u[M],v[M];
int col,now,top,dfn[N],low[N],color[N],sta[N],si[N];
int rd[N],cd[N],dep[N],sum[N];
bool f[N];
struct edge{int next,from,to;}e[M];
struct node{int u,v;}C[M],b[M];

inline bool cmp(node a,node b){return (a.u<b.u || a.u==b.u && a.v<b.v|| a.u==b.u && a.v==b.v);}
inline void add(int u,int v){cnt++;e[cnt].next=head[u];e[cnt].to=v;head[u]=cnt;}

inline void tarjan(int u)
{
    dfn[u]=low[u]=++now;
    sta[++top]=u;	
    for (register int i=head[u]; i; i=e[i].next)
    {
        if (!dfn[e[i].to])
        {
            tarjan(e[i].to);
            low[u]=min(low[u],low[e[i].to]);
        }
        else if (!color[e[i].to])
        low[u]=min(low[u],dfn[e[i].to]);
    }
    if (low[u]==dfn[u])
    {
        color[u]=++col;
        si[col]++;
        while (sta[top]!=u) color[sta[top]]=col,si[col]++,top--;
        top--;
    }
}

inline void dfs(int u,int fa)
{
	f[u]=true;
	if (!cd[u]) {dep[u]=si[u]; sum[u]=1; return;}
	for (register int i=head[u]; i; i=e[i].next)
	if (e[i].to!=fa)
	{
		if (!f[e[i].to]) dfs(e[i].to,u);
		if (dep[e[i].to]+si[u]>dep[u]) dep[u]=dep[e[i].to]+si[u],sum[u]=sum[e[i].to]%MOD;
		else if (dep[e[i].to]+si[u]==dep[u]) sum[u]=(sum[u]+sum[e[i].to])%MOD;
	}
}

int main(){
memset(head,0,sizeof(head));
memset(dfn,0,sizeof(dfn));
	scanf("%d%d%d",&n,&m,&MOD);
	for (register int i=1; i<=m; ++i) scanf("%d%d",&u[i],&v[i]),add(u[i],v[i]);
	
//缩点    
    for (register int i=1; i<=n; ++i) if (!dfn[i]) tarjan(i);


//离散化去重
for (register int i=1; i<=m; ++i) 
if (color[u[i]]!=color[v[i]]) k++,C[k].u=color[u[i]],C[k].v=color[v[i]];
sort(C+1,C+k+1,cmp);
cnt=0; 
cnt++; b[cnt].u=C[1].u,b[cnt].v=C[1].v; now1=b[cnt].u,now2=b[cnt].v;
for (register int i=2; i<=k; ++i) if (C[i].u!=now1|| C[i].v!=now2) 
cnt++,b[cnt].u=C[i].u,b[cnt].v=C[i].v,now1=b[cnt].u,now2=b[cnt].v;


//重新建图
	memset(head,0,sizeof(head));
	memset(e,0,sizeof(e));
	for (register int i=1; i<=cnt; ++i) 
	{
	cd[b[i].u]++,rd[b[i].v]++;
	e[i].next=head[b[i].u];
	e[i].from=b[i].u;
	e[i].to=b[i].v;
	head[b[i].u]=i;
	}


//记忆化搜索
	for (register int i=1; i<=col; ++i) if (!rd[i] && !f[i]) dfs(i,0); 



//统计答案
MAX=0,ans=0;	
	for (register int i=1; i<=col; ++i)
	{
		if (dep[i]>MAX) 
		{	
		MAX=dep[i];
		ans=sum[i];
		}
		else
		if (MAX==dep[i])
		ans=(ans+sum[i])%MOD;
	}   
    
    
	printf("%d\n",MAX);
	printf("%d\n",ans);
return 0;
}

例题四： 恒星亮度 link

思路：
差分约束系统+Tarjan缩点+拓扑DP

设$di{s}_i$表示恒星i的亮度，分类讨论五种情况：

1. $di{s}_a$=$di{s}_b$时，我们可以看成是$di{s}_a$>=$di{s}_b$和$di{s}_b$>=$di{s}_a$两个条件
2. $di{s}_a$>$di{s}_b$时，我们看成是$di{s}_a$>=$di{s}_b+1$(再整数值域内二者等价)。
3. $di{s}_a$>=$di{s}_b$时，我们同样可以看成是$di{s}_a$>=$di{s}_b+0$
4. $di{s}_b$>=$di{s}_a$时，那我们转换一下，把b看成a，就是情况3
5. $di{s}_b$>$di{s}_a$时，就是情况2

总结一下，所以的约束条件都可以看成是$di{s}_a$>=$di{s}_b+x$的形式。
怎么缩呢，我们考虑把 A 小于或小于等于 B 连一条从 A 到 B 的有向边。
然后缩在一起的就是亮度相同的。
然后你会想到如果一个环中有一条边是由小于构成的，
那就出问题了。（因为你又要求亮度相同，然后你这个地方由不能让亮度相同，那就出矛盾了）
那你就把边分成两类，可以参与缩点的和不可以参与的。
然后你也正常缩点（不然变成不了 DAG），
然后建缩点后的图的时候如果一条边是不能参与缩点的，
但是它的两边在缩点后属于同一个的话，就说明矛盾，就无解了。
然后你就会发现 DAG 的起始点可能不止一个，但是问题不大，就都设为亮度是 1 不久好了吗。
然后就会想到用拓扑序 DP，然后你在转移的时候判断一下你转移的边的类型，
如果是小于的就是原来的 +1，否则就是原来的