【C语言】经典题目(四)

HI，大家好~这是一篇C语言经典题目的博客。
更多C语言经典题目及刷题篇，可以参考：
【C语言】经典题目(一)
【C语言】经典题目(二)
【C语言】经典题目(三)
【C语言】字符串刷题篇

本篇文章主要利用函数完成所需的功能及程序的编写。
主要有：
①写一个函数判断一个数是不是素数。
②写一个函数判断一年是不是一年。
③写一个函数，实现一个整型有序数组的二分查找。
④写一个函数，每调用一次这个函数，num值就会增加1。

打印100~200之间的素数

✨思路：首先，自定义函数，判断一个数是不是素数。在主函数中，对100~200个数依次利用所写的函数进行判断。如果是，则打印。如果是素数，则count+1，可以计算出100-200之间有多少个素数。
✨对于我们自定义的判断素数的函数，它的结果只有两种，是和不是。
①如果是素数，我们可以返回 1，如果不是素数，我们返回 0。
②对于判断一个数是不是素数这样的问题，它只有两种情况，是和不是，即True和False。所以这个题目，我们可以定义我们的函数类型是布尔类型，返回True或者False。但要注意，包含头文件

①代码实现：

#define _CRT_SECURE_NO_WARNINGS 1
#include 
#include 
int is_prime(int n)
{
	int i;
	for (i = 2; i <= sqrt(n); i++)
	{
		if (n % i == 0)
			return 0;
	}
	return 1;
}
int main(void)
{
	int i;
	int count = 0;
	for (i = 101; i < 200; i = i + 2)
	{
		if (is_prime(i)) 
		{
			printf("%d ", i);
			count++;
		}
	}
	printf("\n");
	printf("count=%d", count);
	return 0;
}

运行结果：

②代码实现

#define _CRT_SECURE_NO_WARNINGS 1
#include 
#include 
#include 
bool is_prime(int n)
{
	int i;
	for (i = 2; i <= sqrt(n); i++)
	{
		if (n % i == 0)
			return false;
	}
	return true;
}
int main(void)
{
	int i;
	int count = 0;
	for (i = 101; i < 200; i = i + 2)
	{
		if (is_prime(i))
		{
			printf("%d ", i);
			count++;
		}
	}
	printf("\n");
	printf("count=%d", count);
	return 0;
}

打印1000~2000之间的闰年

✨思路：首先先写一个自定义函数判断一年是不是闰年。对于主函数，遍历1000-2000,对每一个年份利用所编写的函数进行判断。如果是，则打印。如果是，count+1，可以计算1000~2000之间闰年年份的个数。
✨对于我们自定义的判断是否是闰年的函数，它的结果也只有两种，是和不是。如同上面的题目一样
①如果是闰年，我们可以返回 1，如果不是闰年，我们返回 0。
②定义我们的函数类型是布尔类型，如果是闰年，返回True如果不是，返回False。要注意，包含头文件**
①代码实现

#define _CRT_SECURE_NO_WARNINGS 1
#include 
int is_leap_year(int year)
{
	if (year % 400 == 0 || year % 4 == 0 && year % 100 != 0)
		return 1;
	else
		return 0;
}
int main()
{
	int i;
	int count = 0;
	for (i = 1000; i <= 2000; i ++)
	{
		if (is_leap_year(i))
		{
			printf("%d ", i);
			count++;
		}
	}
	printf("\ncount=%d\n", count);
	return 0;
}

②代码实现

#define _CRT_SECURE_NO_WARNINGS 1
#include 
#include 
bool is_leap_year(int year)
{
	if (year % 400 == 0 || year % 4 == 0 && year % 100 != 0)
		return true;
	else
		return false;
}
int main()
{
	int i;
	int count = 0;
	for (i = 1000; i <= 2000; i ++)
	{
		if (is_leap_year(i))
		{
			printf("%d ", i);
			count++;
		}
	}
	printf("\ncount=%d\n", count);
	return 0;
}

写一个函数，实现一个有序数组的二分查找

详解二分查找

✨首先，我们先抛开在函数中实现有序数组的二分查找这个问题。
我们先来探索一下如何用代码实现二分查找。
假如我们给上一个如下的有序数组:

假设我们要查找的数字为5.
①我们要将5与这个有序数组的中间值进行比较：

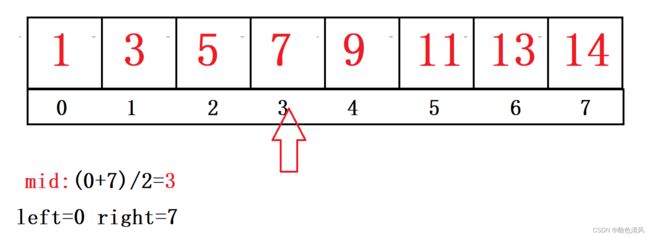
而目标数5<7,下一步我们缩小二分查找的范围。
②缩小二分查找的范围

③进行下一次的二分查找:

而目标数5>3,接着我们再次缩小二分查找的范围。
④再次缩小二分查找的范围：

⑤进行二分查找

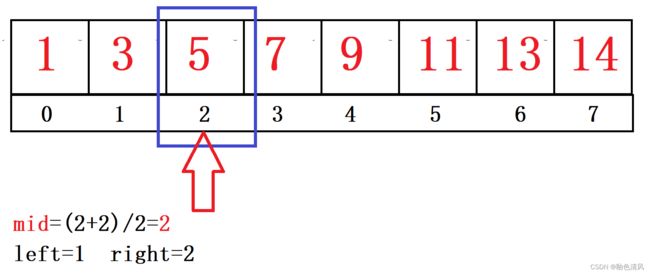
而目标数==mid，所以我们在这个有序数组中找到了。

✨总结：在一个有序数组中进行二分查找，我们是与中间值进行比较的，如果不相等，我们一步一步的缩小二分查找的范围。就像是一个数组的两个指针在进行一步一步移动，直到两个指针正好指的是同一个数时，那就必须要停止查找了，如果这时还没有找到，说明在这个数组中就没有了。
✨将上述的文字转化为代码描述：在数组中，将中间数mid和目标数进行比较，如果相等，则找到了，如果不相等，进一步更新修改缩小数组，对于新数组同样进行上述的过程…在产生新的数组，在进行判断…所以我们需要写一个循环，循环的条件就是left<=right。
代码实现:

#define _CRT_SECURE_NO_WARNINGS 1
#include 
int main()
{
	int arr[10] = { 1,2,3,4,5,6,7,8,9,10 };
	int n = 0;
	int right = 0, left = 0, mid = 0;
	int flag = 0;
	printf("你想要查找的数字:");
	scanf("%d", &n);
	//初始化
	left = 0; right = 9; mid = (left + right) / 2;

	while (left <= right)
	{
		if (arr[mid] == n)
		{
			printf("找到了\n");
			printf("下标是%d", mid);
			flag = 1;
			break;
		}
		else if (n < arr[mid])
		{
			right = mid - 1;    //left不变
			mid = (right + left) / 2;
		}
		else
		{
			left = mid + 1;  //right 不变
			mid = (right + left) / 2;
		}

	}
	if (flag = 0)
		printf("没找到");
	return 0;
}

函数实现二分查找

✨首先我们需要自定义一个函数，在函数内需要对一个数组实现二分查找。
函数参数我们需要一个数，即我们的目标数，和一个数组首元素的地址。
✨对于函数的返回值，因为我们不仅仅是想知道在数组中有没有目标数，更想明确它的下标，所以函数的返回值，我们不妨返回的是下标。若是没有找到的话，那就返回一个负数-1即可。（因为不会有数组元素的下标为负数的。）
✨然后我们在主函数中调用函数，传递参数即可。

#define _CRT_SECURE_NO_WARNINGS 1
#include 
int binary_search(int n, int arr[],int sz)
{
	int left = 0, right = sz-1;
	int mid = (left + right) / 2;
	while (left <= right)
	{
		if (arr[mid] == n)
			return mid;
		else if (arr[mid] > n)
		{
			right = mid - 1;//left不变
			mid = (left + right) / 2;
		}
		else
		{
			left = mid + 1;//right不变
			mid = (left + right) / 2;
		}
	}
	return  -1;
}
int main()
{
	int n = 0;
	int arr[10] = { 1,4,6,7,9,11,14,16,18,19 };
	printf("你想要查找的数字:\n");
	int sz = sizeof(arr) / sizeof(arr[0]);
	scanf("%d", &n);
	int ret = binary_search(n, arr,sz);
	if (ret>-1)
	{
		printf("找到了\n");
		printf("下标为%d", ret);
	}
	else
		printf("没找到\n");
	return 0;
}

运行结果:

写一个函数，没调用一次这个函数，就会将num的值增加1

✨因为每调用一次函数，就要将num的变化，而能使得num变化，我们需要向函数传递num的地址，使得每调用一次，就能使num的值发生变化。
代码实现：

#define _CRT_SECURE_NO_WARNINGS 1
#include 
void Add(int* p)
{
	*p = *p + 1;
}
int main()
{
	int num = 3;
	Add(&num);
	printf("%d\n", num);
	Add(&num);
	printf("%d\n", num);
	Add(&num);
	printf("%d\n", num);
	return 0;
}

运行结果: